Практическая работа №1-2 Тема: Приближенные вычисления
Цель: сформировать у студентов знания, умения и навыки работы с приближенными числами в применении формул погрешностей элементарных действий и функций, нахождения значений выражений по способу границ и методом строгого учета абсолютных погрешностей после каждой операции.
Форма организации занятия – индивидуальная.
Студент должен
знать:
уметь:
вычислять абсолютную и относительную погрешность;
применять формулы погрешности арифметический действий;
применять формулы погрешности элементарных функций.
Содержание отчета о работе:
Вариант определяется согласно контрольному списку.
Все задания (1-3) выполняются письменно, указываются результаты всех промежуточных вычислений.
При оценивании учитывается правильность и аккуратность выполнения задания.
Методические указания:
ех – абсолютная погрешность.
δх – относительная погрешность.
х – точное значение величины.
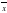 - приближенное значение величины (приближение)
- приближенное значение величины (приближение)
ех = |х - 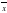 |
| 
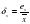
Пример 1. Дано число х=0,00006 и его приближение 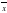 =0,00005. Найти абсолютную и относительную погрешности приближения.
=0,00005. Найти абсолютную и относительную погрешности приближения.
Решение: ex = | 0,00006-0,00005| = 0,00001
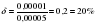
Ответ: абсолютная погрешность 0,00001 и относительная погрешность приближения равна 20%
Пример 2. Найти предельные абсолютные и относительные погрешности числа х = 984,6, если оно имеет только верные цифры в строгом смысле.
Решение:
Цифры числа верны в строгом смысле, если абсолютная погрешность данного числа не превосходит половины единицы разряда, в котором записана последняя верная цифра числа.
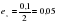 ( т.к. 6 –последняя верная цифра, стоит в разряде десятых)
( т.к. 6 –последняя верная цифра, стоит в разряде десятых)
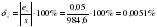
Ответ: абсолютная погрешность для числа х ех=0,05
относительная погрешность числа х δх=0,0051
Пример 3. Найти предельные абсолютные и относительные погрешности числа х =2,364, если оно имеет только верные цифры в широком смысле.
Решение:
Цифры числа верны в широком смысле, если абсолютная погрешность данного числа не превосходит единицы разряда, в котором записана последняя верная цифра числа.
ех = 0,001 (последняя цифра 4 - разряд тысячных)
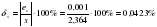
Ответ: абсолютная погрешность для числа х ех = 0,001
относительная погрешность числа х δх = 0,0423%.
Погрешность округленного числа.
Пример 4: Округляя число х=1,1426 до четырех значащих цифр, определить абсолютную и относительную погрешности полученных приближений. Цифры верны в широком смысле.
Решение:
По определению верной цифры в широком смысле абсолютная погрешность ех=0,0001
Округлим число х до четырех значащих цифр: х1=1,143
Погрешность округленного числа равна сумме погрешности исходного числа и погрешности округления:
Δокр=| 1,143-1,1426| = 0,0004
ех1= 0,0004+0,0001=0,0005
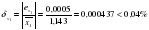
Пример5: Число х, все цифры которого верны в строгом смысле округлить до трех значащих цифр после запятой. Для полученного результата х1 вычислить границу абсолютной и относительной погрешностей. В записи числа х1 указать количество верных цифр погрешности. х=1,1426
Решение:
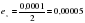
х1=1,143
ех1= ех + Δокр
Δокр= | 1,143-1,1426| = 0,0004
ех1= 0,00005+0,0004=0,00045
Значит в числе 1,143 цифры верны в строгом смысле до тысячных по абсолютной погрешности.
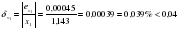
Вычислительная погрешность
1. Погрешность суммирования чисел х ± ех, у±еу
Абсолютная погрешность:
z =( х ± ех)+ (у±еу)=(x + y) ± ( ех + еу)
Относительная погрешность:
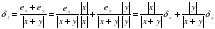
2. Погрешность вычитания чисел х ± ех, у±еу
Абсолютная погрешность:
z =( х ± ех)- (у±еу)=(x - y) ± ( ех + еу)
Относительная погрешность:
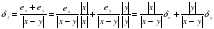
3. Погрешность умножения чисел х ± ех, у±еу
Абсолютная погрешность:
z =( х ± ех)* (у±еу)=ху±уех±хеу±ехеу ≈ ху±уех±хеу
Относительная погрешность:
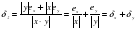
4. Погрешность деления чисел х ± ех, у±еу
Абсолютная погрешность:
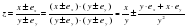
Относительная погрешность:
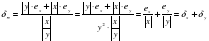
Погрешности элементарных функций.
Погрешность функции, зависящей от одной переменной.
Абсолютная погрешность:
f(х ± ех) ≈ f(x) ± f ’(x)ex
Δf = f(х ± ех) - f(х)=| f ’(х)|ex
Относительная погрешность:
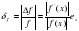
Пример 6: Исходные числовые значения аргумента заданы цифрами, верными в строгом смысле. Найти абсолютную и относительную погрешности функции f(x)=cos(0,47). Определить количество верных цифр в строгом смысле по относительной погрешности. В ответе сохранить верные цифры и одну сомнительную.
Решение:
Найдем значение функции f(x)=cos(0,47)=0,891568
абсолютная погрешность:
Δf = | f ’(х)|ex
1) | f ’(х)| = sin(0,47)=0,452886285
2) e0,47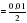 =0,005
=0,005
3) Δf=0,452886285*0,005=0,00226443.
Относительная погрешность:
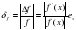
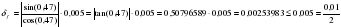
Значит в числе 0,891568 две цифры после запятой верны в строгом смысле.
Ответ: 0,892
Пример 7. Вычислить значение величины с помощью метода строгого учета границ абсолютных погрешностей после каждой операции, цифры верны в строгом смысле.
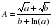 , если а = 12,34, b= 14,3
, если а = 12,34, b= 14,3
Решение:
Для получения значения величины А необходимо выполнить 6 действий. Будем вычислять абсолютную погрешность после каждого действия с целью определения количества верных цифр в промежуточных результатах.
| a | b | 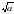
| 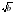
| 
| ln(a) | b+ln(a) | A |
| 12,34 | 14,3 | 3,513 | 3,78 | 7,29 | 2,5128 | 16,8 | 0,434 |
| ea | eb | 
| 
| 
| 
| 
| еА |
| 0,005 | 0,05 | 0,00071 | 0,0066 | 0,0073 | 0,00041 | 0,050 | 0,0017 |
При пооперационном строгом учете ошибок промежуточные результаты после округления до одной запасной (с учетом вычисленной параллельно величины погрешности) и их погрешности заносят в таблицу
Значения погрешностей для удобства округлим до двух значащих цифр по избытку и тоже занесем в таблицу.
Цифры даны верными в строгом смысле, значит еа=0,005, ев=0,05
Найдем 
Абсолютная погрешность равна 
Из полученного значения погрешности видно, что в результате верны две значащие цифры после запятой, т.е.
 ( сохраняем одну сомнительную цифру)
( сохраняем одну сомнительную цифру)
Найдем 
Абсолютная погрешность равна
Из полученного значения погрешности видно, что в результате верна одна значащая цифра после запятой, т.е.
 ( сохраняем одну сомнительную цифру)
( сохраняем одну сомнительную цифру)
Найдем
z =( х ± ех)+ (у±еу)=(x + y) ± ( ех + еу)= (3,513+3,78) ± (0,00071+0,0066) = 7,293 ± 0,00731
т.к. 0,00731
Найдем ln(a)= ln(12,34)=2,51285
Абсолютная погрешность: 
В числе 2,512846 верны три значащие цифры после запятой, т.е.
ln(12,34)=2,512846 ≈ 2,5128( сохраняем одну сомнительную цифру)
Найдем b + ln(a ) = (14,3 + 2,5128 ) ± (0,05+0,00041) = 16,8128 ± 0,050405
Т.к.  , то в числе 16,8128 верны цифры до единиц 16,8128 ≈ 16,8 (сохраняем одну сомнительную цифру)
, то в числе 16,8128 верны цифры до единиц 16,8128 ≈ 16,8 (сохраняем одну сомнительную цифру)
Найдем А
Округлим результат А до двух верных цифр после запятой, получим окончательный ответ: А=0,434 (сохраняем одну сомнительную цифру)
Ответ: А = 0,434 ± 0,002
Погрешности значений элементарных функций.
Таблица 1
| Функция | Абсолютная погрешность | Относительная погрешность |
| 
| 
| 
|
| 
| 
| 
|
| sin(x) | |cos(x)| ex | |ctg(x)| ex |
| cos(x) | |sin(x)| ex | |tg(x)| ex |
| tg(x) | 
| 
|
| ln(x) | 
| 
|
| lg(x) | 
| 
|
| ex | ex ex | 
|
| 10x | 
| 
|
| xy | 
| 
|
| arcsin(x) | 
| 
|
| arctg(x) | 
| 
|
Задания для практического занятия №1.
Задание №1.
Найти предельные абсолютные и относительные погрешности чисел, если они имеют только верные цифры:
а) в строгом смысле; б) в широком смысле.
| № варианта | а) | б) |
| № варианта | а) | б) |
| 1 | 11,445 | 2,043 | 16 | 112,5 | 0,04453 |
| 2 | 8,345 | 0,288 | 17 | 0,576 | 2,5008 |
| 3 | 0,374 | 4,348 | 18 | 25,613 | 0,0748 |
| 4 | 41,72 | 0,678 | 19 | 0,4223 | 0,57 |
| 5 | 18,357 | 2,16 | 20 | 112,45 | 3,4 |
| 6 | 14,862 | 8,73 | 21 | 2,4516 | 0,863 |
| 7 | 0,3648 | 21,7 | 22 | 5,6432 | 0,00858 |
| 8 | 0,5746 | 236,58 | 23 | 12,688 | 4,636 |
| 9 | 5,634 | 0,0748 | 24 | 15,644 | 6,125 |
| 10 | 20,43 | 0,576 | 25 | 16,383 | 5,734 |
| 11 | 12,45 | 3,4453 | 26 | 18,275 | 0,00644 |
| 12 | 2,3445 | 0,745 | 27 | 3,75 | 6,8343 |
| 13 | 0,5746 | 42,884 | 28 | 26,3 | 4,8556 |
| 14 | 3,4 | 0,078 | 29 | 43,813 | 0,645 |
| 15 | 2,4342 | 0,57004 | 30 | 3,643 | 72,385 |
Задание №2.
Число х, все цифры которого верны в строгом смысле, округлить до трех значащих цифр. Для полученного результата х1≈х вычислить границы абсолютной и относительной погрешностей. В записи числа х1 указать количество верных цифр по погрешности.
| № варианта | х |
| № варианта | х |
| 1 | 3549 | 16 | 9,2038 |
| 2 | 32,147 | 17 | 2,3143 |
| 3 | 0,0002568 | 18 | 0,012147 |
| 4 | 7,544 | 19 | 0,86129 |
| 5 | 198,745 | 20 | 0,1385 |
| 6 | 37, 4781 | 21 | 23,394 |
| 7 | 0,183814 | 22 | 0,003775 |
| 8 | 0,009145 | 23 | 718,21 |
| 9 | 11,3721 | 24 | 9,73491 |
| 10 | 0,2538 | 25 | 11,456 |
| 11 | 10,2118 | 26 | 0,1495 |
| 12 | 4,394 | 27 | 6,2358 |
| 13 | 0,8437 | 28 | 4,4005 |
| 14 | 129,66 | 29 | 2,3078 |
| 15 | 48,847 | 30 | 3,2175 |
Задание № 3
Вычислить значение величины Z при заданных значениях чисел a,b,c используя систематический учет абсолютных погрешностей после каждой операции, а также с помощью метода границ. Найти абсолютную и относительную погрешности z и определить по ним количество верных цифр в z, если цифры a,b,c верны в строгом смысле.
| № варианта | Задание | Исходные данные | № варианта | Задание | Исходные данные |
| 1 | 
| a = 0,0399 b = 4,83 c = 0,0721 | 16 | z = a2+sin(b-ln(c)) | a =8,317 b = 13,521 c = 6,123 |
| 2 | 
| a =5,52 b =3,27 c =14,123 | 17 | 
| a = 0,038 b = 3,9353 c = 5,75 |
| 3 | 
| a =2,258 b =0,027 c =9,87 | 18 | 
| a = 7,345 b = 0,31 c = 0,09871 |
| 4 | 
| a =1,0574 b =1,40 c =1,1236 | 19 | 
| a =0,2471 b =0,0948 c =4,378 |
| 5 | 
| a =3,49 b =0,845 c =0,0037 | 20 | 
| a = 1,284 b = 4,009 c = 3,2175 |
| 6 | 
| a =0,0976 b =2,371 c =1,15887 | 21 | 
| a = 18,407 b = 149,12 c = 2,3078 |
| 7 | 
| a =82,3574 b =34,12 c =7,00493 | 22 | 
| a = 29,49 b = 87,878 c = 4,403 |
| 8 | 
| a =3,71452 b =3,03 c =0,756 | 23 | 
| a = 74,079 b = 5,3091 c = 6,234 |
| 9 | 
| a =0,11587 b =4,256 c =3,00971 | 24 | 
| a =3,4 b =6,22 c =0,149 |
| 10 | 
| a = 4,05 b = 6,723 c = 0,03254 | 25 | 
| a =5,387 b =13,527 c =0,7565 |
| 11 | 
| a = 0,7219 b = 135,347 c =0,013 | 26 | 
| a = 1,75 b = 1,215 c = 0,041 |
| 12 | 
| a = 0,113 b = 0,1056 c = 89,4 | 27 | 
| a =3,672 b =4,63 c =0,0278 |
| 13 | 
| a = 1,247 b = 0,346 c = 0,051 | 28 | 
| a =0,317 b =13,57 c =0,751 |
| 14 | 
| a = 18,035 b = 3,7251 c = 0,071 | 29 | 
| a =0,317 b =33,827 c =14,85 |
| 15 | 
| a = 0,317 b = 3,27 c = 4,7561 | 30 | 
| a =12,72 b =0,34 c =0,0290 |
Вопросы по теме:
Что такое абсолютная и относительная погрешности?
Как классифицируют виды погрешностей?
Что значит цифра, верная в строгом, широком смыслах?
Как находится погрешность округленного числа?
Как определить количество верных цифр по абсолютной погрешности.
Литература:
Лапчик М.П. Элементы численных методов: учебник для студ. сред. проф. образования М.:Издательский центр» Академия 2007
Бахвалов Н.С. , Жидков Н.П. Кобельков Г.М. Численные методы. – М.: Лаборатория Базовых Знаний, 2001. – С.35-75.
Плотников А.Д. Численные методы Минск ООО «Новое знание» 2007
Поршнев С.В., Беленкова И.В. Численные методы на базе Mathcad. – СПб.: БХВ-Петербург, 2005. – 464 с.:ил.







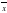 - приближенное значение величины (приближение)
- приближенное значение величины (приближение)
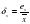
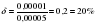
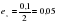 ( т.к. 6 –последняя верная цифра, стоит в разряде десятых)
( т.к. 6 –последняя верная цифра, стоит в разряде десятых)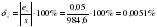
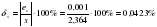
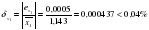
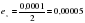
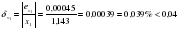
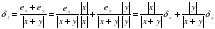
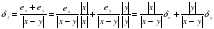
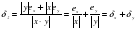
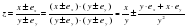
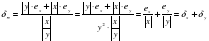
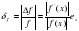
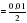 =0,005
=0,005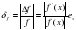
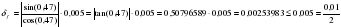
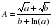 , если а = 12,34, b= 14,3
, если а = 12,34, b= 14,3