Практико – ориентированные задания на уроках математики.

Применение Практико – ориентированных заданий

«Скажи мне - и я забуду. Покажи мне - и я запомню. Дай мне действовать самому - и я научусь»

Конфуций

Пилипенко О.А.

МОУ «СОШ №21 имени И.М.Каплунова», г.Энгельс

Решение практико-ориентированных задач на уроках математики должно иметь конкретные цели:

• - Научиться решать задачи, с которыми каждый из нас может столкнуться в повседневной жизни.
• - Опровергнуть мнение, что не всем нужно учиться математике.
• - Доказать, что математика нужна всем, чем бы человек не занимался, какой бы профессией не овладевал, где бы не учился.
• - Готовиться ко Всероссийским проверочным работам(ВПР), ОГЭ, ЕГЭ (Единому Государственному Экзамену), в которые входят практико-ориентированные задачи.

Методика обучения решению практико-ориентированных задач в курсе математики

К этапам решения можно отнести:

1) анализ текста задачи;

2) перевод текста на язык математики;

3) установление отношений между данными и вопросом;

4) составление плана решения задачи;

5) осуществление плана решения;

6) проверка и оценка решения задачи.

Методика работы с практико-ориентированной задачей на конкретных примерах 5-6,8,9 классов.

Задача 1.

Через 2 крана бак наполняется за 9 минут. Если бы был открыт только первый кран, то бак наполнился бы за 36 минут. За сколько минут наполнился бы бак через один второй кран?

Работа над текстом задачи.

Задаем вопросы:

• Что происходит в задаче?
• Известно ли время за которое наполняется бак с помощью двух кранов?
• С помощью первого крана?
• С помощью второго крана?
• Через второй кран бак будет наполняться больше или меньше девяти минут?
• Какая часть бака наполняется за 1 минуту 2 кранами вместе?
• Какая часть бака наполняется 1 краном за 1минуту?

Перевод текста на математический язык, установление соотношений между данными и вопросом .

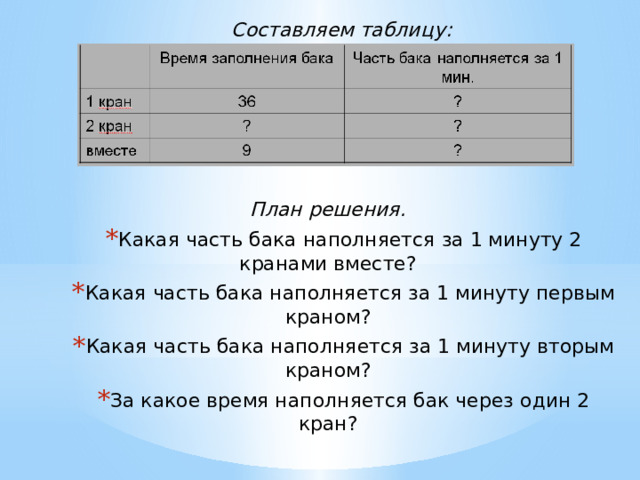
Составляем таблицу:

План решения.

• Какая часть бака наполняется за 1 минуту 2 кранами вместе?
• Какая часть бака наполняется за 1 минуту первым краном?
• Какая часть бака наполняется за 1 минуту вторым краном?
• За какое время наполняется бак через один 2 кран?

По окончанию решения задачи делаем проверку и оценку решения задачи, задавая такие вопросы учащимся:

• Что показалось трудным в решении задачи?
• Есть ли другие способы решения?
• Придумать похожую задачу про заполнение бассейна.

Применение практико-ориентированных задач в

8 классе на примере теоремы Пифагора.

Теорема Пифагора в стихах

Приемы решения практико-ориентированных задач

нового типа ОГЭ

Что нужно уметь

• Выделять ключевые фразы и основные вопросы из текста заданий.
• Уметь выполнять арифметические действия с натуральными числами, десятичными и обыкновенными дробями, производить возведение числа в степень, извлекать арифметический квадратный корень из числа.
• Уметь переводить единицы измерения.
• Уметь округлять числа.
• Уметь находить число от процента и проценты от числа.
• Уметь находить часть от числа и число по его части.
• Применять основное свойство пропорции.
• Уметь решать уравнения, неравенства.
• Разбираться в изображениях рисунков, планов и масштабе фигур на рисунках.
• Анализировать и пользоваться информацией из таблиц.
• Анализировать и пользоваться заданными графиками.

Что нужно знать

Формулы геометрии:

Периметр прямоугольника: Р=2(а +b)

Периметр квадрата: Р =4а

Длину окружности: С= 2ПR

Объем параллелепи педа: V= abc

Площади фигур:

Площадь прямоугольника: S = ab

Площадь квадрата: S = а 2

Площадь круга: S = ПR 2

теорему Пифагора: c 2 = a 2 + b 2

Формулы синуса, косинуса, тангенса острого угла в прямоугольном треугольнике

Задачи о дачном участке

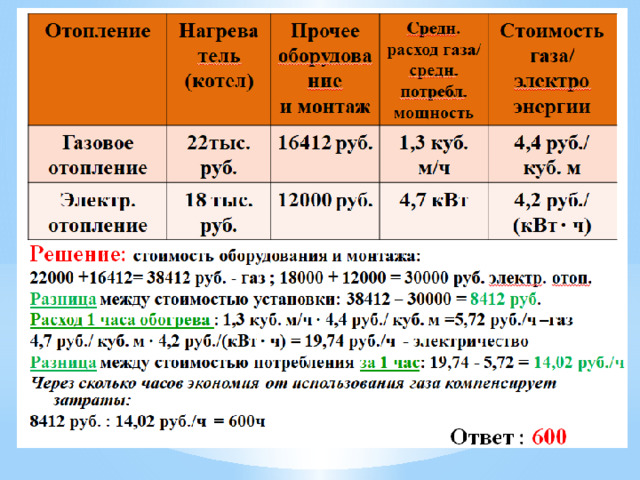
Задачи про шины

Задачи про форматы листов

Общепринятые форматы листов бумаги обозначают буквой A

и цифрой: A0, A1, A2 и так далее. Если лист формата A0

разрезать пополам, получаются два листа формата A1.

Если лист A1 разрезать пополам, получаются два листа

формата A2 и так далее . При этом отношение длины листа

к его ширине у всех форматов, обозначенных буквой A, одно

и то же (то есть листы всех форматов подобны друг другу).

Это сделано специально — чтобы можно было сохранить

пропорции текста на листе при изменении формата бумаги

(размер шрифта при этом тоже соответственно изменяется).

Задачи о теплице

Сергей Петрович решил построить на дачном участке

теплицу длиной 4м . Для этого сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 5м

каждая и покрытие для обтяжки. Отдельно требуется купить пленку для передней и задней стенок теплицы. В передней стенке планируется вход , показанный на рисунке

прямоугольником ВСС1В1 , где точки В,О,С делят отрезок АD

на четыре равные части. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы – одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 40см , для которых необходимо купить тротуарную плитку размером 20смХ20см .

Задачи о земледелии в горных районах

Задачи о мобильном интернете и тарифе

Три группы практико-ориентированных задач

1 группа-это задачи профориентационного направления.

(для штурмана направление движения судна, для инженера-оптика - мощность луча маяка и т.п.)».

Примечательно, что в заданиях этой группы создаются ситуации, когда школьник оказывается в определенной роли, что увеличивает возможности определения своей профессии в будущем. Можно использовать готовые задачи, а также можно предложить ученикам самим составить задачи данного направления.

b )надо выгнуть в желоб с квадратным сечением. Исследовать, какой сгиб дает желоб с наибольшим объемом. " width="640"

2 группа - геометрические задачи, связанные с жизнью, с практической деятельностью человека.

• Задача №1 . На берегу реки требуется построить водонапорную башню для снабжения водой двух сел так, чтобы общая длина труб от водонапорной башни до обоих сел была наименьшей.

• Задача №2. Необходимо соединить шоссейной дорогой, включая постройку моста через реку, два села. Как должна пройти эта дорога, чтобы путь между селами был кратчайшим.

• Задача №3. Прямоугольный лист жести размером a и b ( b )надо выгнуть в желоб с квадратным сечением. Исследовать, какой сгиб дает желоб с наибольшим объемом.

3 группа – задачи семейно-практического содержания. Например, «один день из жизни семьи»

• Задача № 1.
• Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 8 дней. В одной упаковке 10 таблеток лекарства по 0,25 г. Какого наименьшего количества упаковок хватит на весь курс лечения?
• Задача № 2.
• Пакетик сока стоит 14 рублей 50 копеек. Какое наибольшее число пакетиков сока можно купить на 100 рублей? (Хватит ли денег Вите, если он захочет купить сок себе и угостить пятерых друзей; если «да», то сколько денег у него останется?
• Задача № 3.
• Аня купила месячный проездной билет на автобус. За месяц она сделала 45 поездок. Сколько рублей она сэкономила, если проездной билет стоит 750 рублей, а разовая поездка 25 рублей? 28 рублей?

Удивление –

двигатель учения

Именно удивление влечет и манит, ведет детей к «полету мысли и фантазии», к открытию, к озарению. Не сухой расчет, не вереница огромных цифр, не вызубренные правила и теоремы, а удивительные задачи – вот, что нужно для озарения.