Просмотр содержимого документа
«Презентация для открытого урока алгебры в 10 классе.»

НАХОЖДЕНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЙ НЕПРЕРЫВНОЙ ФУНКЦИИ НА ПРОМЕЖУТКЕ
“ ОСОБЕННУЮ ВАЖНОСТЬ ИМЕЮТ ТЕ МЕТОДЫ НАУКИ, КОТОРЫЕ ПОЗВОЛЯЮТ РЕШАТЬ ЗАДАЧУ, ОБЩУЮ ДЛЯ ВСЕЙ ПРАКТИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ ЧЕЛОВЕКА: КАК РАСПОЛАГАТЬ СВОИМИ СРЕДСТВАМИ ДЛЯ ДОСТИЖЕНИЯ НАИБОЛЬШЕЙ ВЫГОДЫ” ПАФНУТИЙ ЛЬВОВИЧ ЧЕБЫШЕВ.
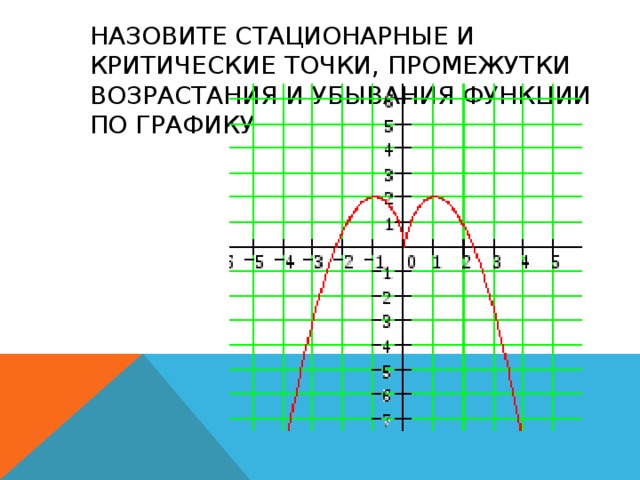
НАЗОВИТЕ СТАЦИОНАРНЫЕ И КРИТИЧЕСКИЕ ТОЧКИ, ПРОМЕЖУТКИ ВОЗРАСТАНИЯ И УБЫВАНИЯ ФУНКЦИИ ПО ГРАФИКУ

НАЗОВИТЕ ПО ДАННЫМ ТАБЛИЦЫ ПРОМЕЖУТКИ ВОЗРАСТАНИЯ И УБЫВАНИЯ ФУНКЦИИ, А ТАК ЖЕ ТОЧКИ МАКСИМУМА И ТОЧКИ МИНИМУМА
x
f´(x)
(-∞; -1)
-
-1
f(x)
(-1; 0)
0
+
-1
0
(0; 2)
0
-
0
2
(2; +∞)
0
+
-3
min
min
max
Сформулируйте признак максимума. Сформулируйте признак минимума.
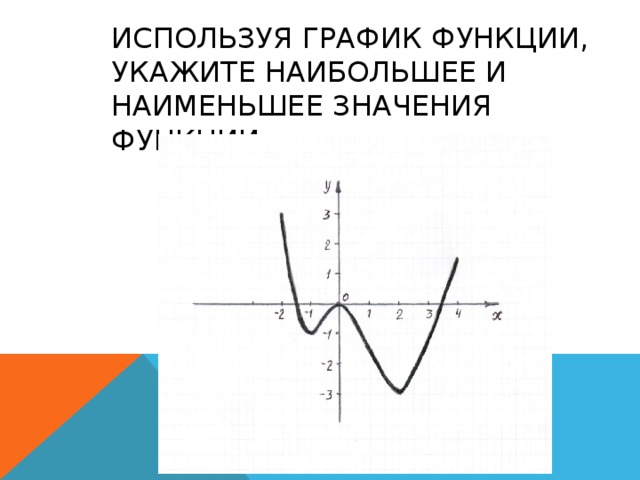
ИСПОЛЬЗУЯ ГРАФИК ФУНКЦИИ, УКАЖИТЕ НАИБОЛЬШЕЕ И НАИМЕНЬШЕЕ ЗНАЧЕНИЯ ФУНКЦИИ.
 0 на (а; b) f(x) – возрастает на [a;b], поэтому наибольшее значение на отрезке функция принимает в точке b ( правом конце промежутка), а наименьшее в точке а ( левом конце промежутка). б) если f´(x) точке а ( левом конце промежутка ), а наименьшее в точке b ( правом конце промежутка ). " width="640"
0 на (а; b) f(x) – возрастает на [a;b], поэтому наибольшее значение на отрезке функция принимает в точке b ( правом конце промежутка), а наименьшее в точке а ( левом конце промежутка). б) если f´(x) точке а ( левом конце промежутка ), а наименьшее в точке b ( правом конце промежутка ). " width="640"
ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ
1) Если функция непрерывна на отрезке, то она достигает на нем и своего наибольшего и своего наименьшего значения.
2) Наименьшего и наибольшего значений непрерывная функция может достигать, как на концах отрезка , так и внутри него.
3) Если наибольшее (или наименьшее) значение достигается внутри отрезка, то только в стационарной или критической точке.
4) Если функция y=f(x) не имеет на отрезке[a;b] критических и стационарных точек, тогда
а) если f´(x)0 на (а; b) f(x) – возрастает на [a;b], поэтому наибольшее значение на отрезке функция принимает в точке b ( правом конце промежутка), а наименьшее в точке а ( левом конце промежутка).
б) если f´(x) точке а ( левом конце промежутка ), а наименьшее в точке b ( правом конце промежутка ).
![АЛГОРИТМ Найти D(f), содержится ли [a;b] в D(f) Определить непрерывность и дифференцируемость функции на D(f) Найти производную f ´(x) Найти стационарные и критические точки функции. Выбрать те , которые лежат внутри отрезка [a;b] Вычислить значения функции y=f(x), в точках, отобранных на пятом шаге и на концах отрезка Выбрать среди этих значений наименьшее ( это будет у наим ) и наибольшее ( это у наиб )](https://fsd.multiurok.ru/html/2018/12/17/s_5c17dc37a413f/img5.jpg)
АЛГОРИТМ
- Найти D(f), содержится ли [a;b] в D(f)
- Определить непрерывность и дифференцируемость функции на D(f)
- Найти производную f ´(x)
- Найти стационарные и критические точки функции.
- Выбрать те , которые лежат внутри отрезка [a;b]
- Вычислить значения функции y=f(x), в точках, отобранных на пятом шаге и на концах отрезка
- Выбрать среди этих значений наименьшее ( это будет у наим ) и наибольшее ( это у наиб )

ТЕОРЕМА: ЕСЛИ ФУНКЦИЯ У=F(X)НЕПРЕРЫВНА НА ПРОМЕЖУТКЕ Х И ИМЕЕТ ВНУТРИ НЕГО ЕДИНСТВЕННУЮ СТАЦИОНАРНУЮ ИЛИ КРИТИЧЕСКУЮ ТОЧКУ Х=Х 0 , ТОГДА:
а)если х=х 0 – точка максимума , то у наиб =f(x 0 );
б) если х=х 0 – точка минимума , то у наим =f(x 0 ).










 0 на (а; b) f(x) – возрастает на [a;b], поэтому наибольшее значение на отрезке функция принимает в точке b ( правом конце промежутка), а наименьшее в точке а ( левом конце промежутка). б) если f´(x) точке а ( левом конце промежутка ), а наименьшее в точке b ( правом конце промежутка ). " width="640"
0 на (а; b) f(x) – возрастает на [a;b], поэтому наибольшее значение на отрезке функция принимает в точке b ( правом конце промежутка), а наименьшее в точке а ( левом конце промежутка). б) если f´(x) точке а ( левом конце промежутка ), а наименьшее в точке b ( правом конце промежутка ). " width="640"
![АЛГОРИТМ Найти D(f), содержится ли [a;b] в D(f) Определить непрерывность и дифференцируемость функции на D(f) Найти производную f ´(x) Найти стационарные и критические точки функции. Выбрать те , которые лежат внутри отрезка [a;b] Вычислить значения функции y=f(x), в точках, отобранных на пятом шаге и на концах отрезка Выбрать среди этих значений наименьшее ( это будет у наим ) и наибольшее ( это у наиб )](https://fsd.multiurok.ru/html/2018/12/17/s_5c17dc37a413f/img5.jpg)












