Презентация "Графы"

Презентация по математике Тема : «Графы»

Группа № 13

Балашов Никита

Содержание

• История возникновения теории графов
• Задача Эйлера о семи мостах
• Виды графов

Исторически сложилось так, что теория графов зародилась двести с лишним лет назад именно в ходе решения головоломок .

Очень долго она находилась в стороне от главных направлений исследований ученых . Первая работа по теории графов, принадлежит известному швейцарскому математику Л . Эйлеру .

История возникновения теории графов

Леонард Эйлер ( 4 (15) апреля 1707 , Базель, Швейцария — 7 (18) сентября 1783, Санкт-Петербург, Российская империя) — швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук.

Эйлер — автор более чем 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др.

Толчок к развитию, теория графов получила на рубеже ХIX и ХХ столетий, когда резко возросло число работ в области топологии и комбинаторики, с которыми ее связывают самые тесные узы родства . Графы стали использоваться при построении схем электрических цепей и молекулярных схем . Как отдельная математическая дисциплина теория графов была впервые представлена в работе венгерского математика Кенига в 30-е годы ХХ столетия .

В последнее время графы и связанные с ними методы исследований органически пронизывают на разных уровнях едва ли не всю современную математику . Теория графов рассматривается как одна из ветвей топологии; непосредственное отношение она имеет также к алгебре и к теории чисел .

Графы эффективно используются в теории планирования и управления, теории расписаний, социологии, математической лингвистике, экономике, биологии, медицине, географии .

Широкое применение находят графы в таких областях, как программирование, теория конечных автоматов, электроника, в решении вероятностных и комбинаторных задач, нахождении максимального потока в сети, кратчайшего расстояния, максимального паросочетания, проверки планарности графа и др . Как особый класс можно выделить задачи оптимизации на графах .

Математические развлечения и головоломки тоже являются частью теории графов, например, знаменитая проблема четырех красок, интригующая математиков и по сей день .

Задача Эйлера о семи мостах

" Некогда мне была предложена задача об острове, расположенном в городе Кенигсберге и окруженном рекой, через которую перекинуто семь мостов. Спрашивается, может ли кто-нибудь непрерывно обойти их, проходя только однажды через каждый мост. И тут же мне было сообщено, что никто еще до сих пор не мог это проделать, но никто и не доказал, что это невозможно. Вопрос этот, хотя и банальный, показался мне, однако, достойным внимания тем, что для его решения недостаточны ни геометрия, ни алгебра, ни комбинаторное искусство. После долгих размышлений я нашел легкое правило, основанное на вполне убедительном доказательстве, с помощью которого можно во всех задачах такого рода тотчас же определить, может ли быть совершен такой обход через какое угодно число и как угодно расположенных мостов или не может.

Задача Эйлера

Виды Графов

Ориентированный граф (кратко орграф ) — (мульти) граф, рёбрам которого присвоено направление. Направленные рёбра именуются также дугами. Записывается в виде G:= (V, A), где V – это не пустое множество вершин или узлов, А - это множество (упорядоченных) пар различных вершин, называемых дугами или ориентированными рёбрами.

Неориентированный граф - записывается в виде G:= (V, E), где V – это не пустое множество вершин или узлов, E - это множество пар (в случае неориентированного графа — неупорядоченных) вершин, называемых рёбрами.

V (а значит и E, иначе оно бы было мультимножеством) обычно считаются конечными множествами.

Многие хорошие результаты, полученные для конечных графов, неверны (или каким-либо образом отличаются) для бесконечных графов . Это происходит потому, что ряд соображений становится ложным в случае бесконечных множеств.

Вершины и рёбра графа называются также элементами графа, число вершин в графе |V| - порядком, число ребер|E| - размером графа.

Смешанный граф – это граф, в котором некоторые ребра могут быть ориентированными, а некоторые – неориентированными. Записывается в виде G:= (V, E, A). Ориентированный и неориентированный графы являются частными случаями смешанного.

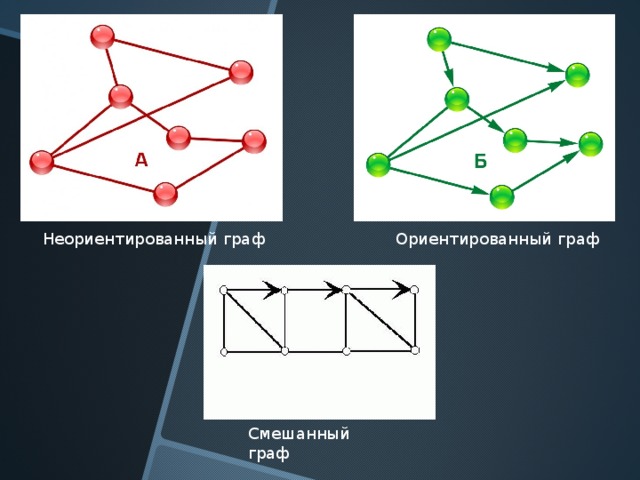
Неориентированный граф

Ориентированный граф

Смешанный граф

Спасибо за внимание !!!