Презентация к теме "Функции"

Функция

Презентация выполнена учителем математики МКОУ Невонская школа

Определение функции.

Функцией называют такую зависимость переменной у от переменной х,

Функция –

при которой

одно из важнейших

каждому значению переменной х соответствует единственное значение переменной у

математических понятий

Функция

Переменную

Переменную

у

x

называют

называют

независимой переменной ,

зависимой переменной

или

аргументом

Говорят также, что

переменная у

является функцией от переменной х

у

D(y) и E(y) функции

Все значения

Все значения ,

независимой переменной

которые принимает

х

образуют

зависимая переменная

область

у

определения функции – D(y)

образуют

область значений

функции – E(y)

Найти D(y) и E(y) функции:

y Є R

• y = 3x-5

x Є R

• y = -2x/3

• y = 3/2x

• y = √1-2x

• y = 11sin x

• y = lg (4x-1)

x Є R

y Є R

x Є (-∞;0)U(0; ∞)

уЄ (-∞;0)U(0; ∞)

x Є (-∞;0,5]

y Є [0; ∞)

x Є R

y Є [-11; 11]

x Є (0,25; ∞)

y Є R

Способы задания функций

1. y=2x-5;

1. Аналитический

2 . Графический

2.

3 . Табличный

3.

4. Описательный

• Функция на [-2; -1] возрастает,

на [0; 4] убывает,

на [-1; 0] равна 5.

x

y

1

2

1

5

4

6

25

36

График функции

Графиком функции

называют множество всех точек координатной плоскости,

абсциссы которых равны значениям аргумента ,

а ординаты - соответствующим значениям функции .

Определите какие из кривых являются графиками функций

y

да

да

y

нет

y

x

x

x

Рис 3

Рис 1

Рис 2

Свойства функций

Свойство графика

1. Чётность:

Функция называется чётной если:

График чётной функции

• D(y) симметрична относительно 0,

симметричен относительно

оси ординат .

• для любого х из D(y) выполняется условие f(x)= f(-x)

Свойства функций

Нечётность

Свойство графика

График нечётной функции

Функция называется

симметричен относительно начала координат .

нечётной если

• D(y) симметрична относительно 0,

• для любого х из D(y) выполняется условие

f(-x)= -f(x)

х 2 f(х 1 )f(х 2 ) [ при х 1 х 2 f(х 1 ) 2 )] " width="640"

Свойства функций

Монотонность

Свойство графика

Функция возрастает

[или убывает] на промежутке I, если для любого х Є I выполняется условие :

при х 1 х 2 f(х 1 )f(х 2 )

[ при х 1 х 2 f(х 1 ) 2 )]

Свойства функций

Знакопостоянство

Свойство графика

Промежутки, на которых функция сохраняет постоянный знак, называются промежутками знакопостоянства

+

+

-

-

-

у

y

4

Графи к функции

E(y)

7

0

3

х

-2

D(y)

Функция у:

Область определения – D(y)= [ - 4; 8].

Область значений – E(y)= [- 2; 5].

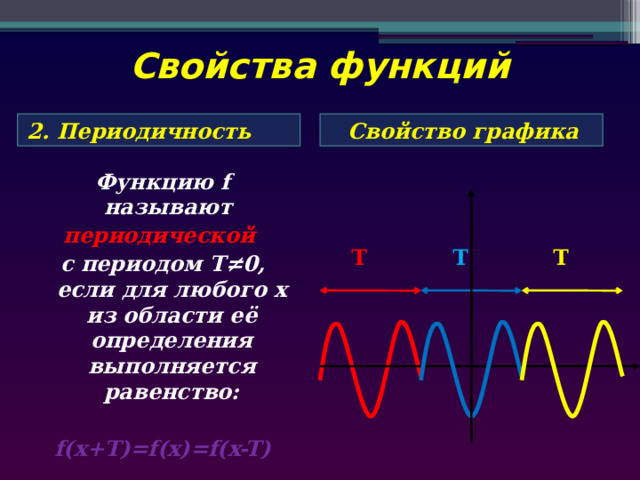
Свойства функций

Свойство графика

2. Периодичность

Функцию f называют

периодической

с периодом Т≠0, если для любого х из области её определения выполняется равенство:

f(x+T)=f(x)=f(x-T)

Т

Т

Т

• Область определения-?
• Область значений-?
• Нули функции-?
• Точки пересечения с осями?
• Промежутки знакопостоянства?

6. Промежутки возрастания?

7. Промежутки убывания?

8. Наибольшее значение функции?

9. Наименьшее значение функции?