Презентация на тему: "Многогранники"

Многогранники

Что такое многогранник?

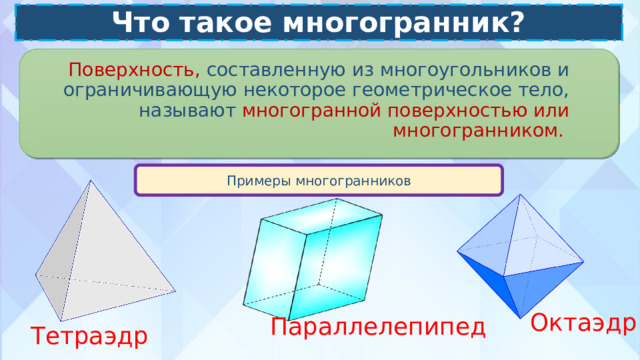
Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, называют многогранной поверхностью или многогранником.

Примеры многогранников

Октаэдр

Параллелепипед

Тетраэдр

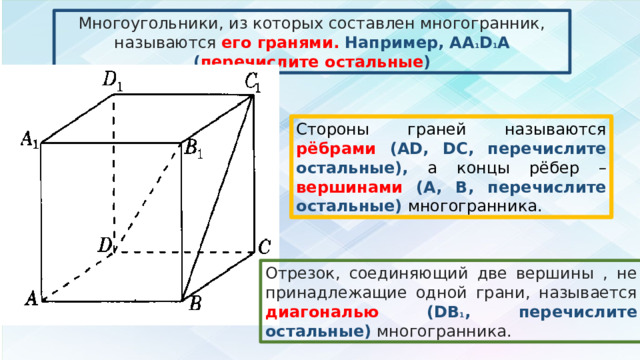
Многоугольники, из которых составлен многогранник, называются его гранями. Например, АА 1 D 1 A ( перечислите остальные )

Стороны граней называются рёбрами (AD, DC, перечислите остальные), а концы рёбер – вершинами (А, В, перечислите остальные) многогранника.

Отрезок, соединяющий две вершины , не принадлежащие одной грани, называется диагональю (DB 1 , перечислите остальные) многогранника.

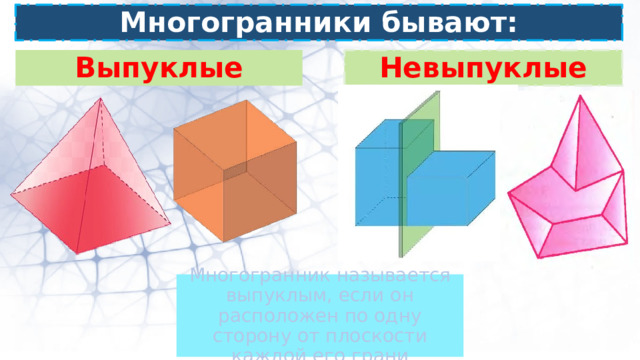
Многогранники бывают:

Выпуклые

Невыпуклые

Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани

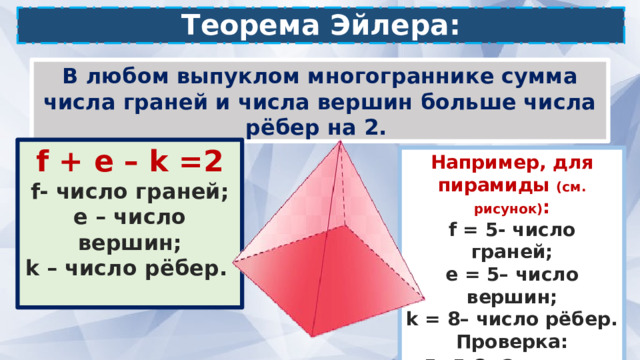
Теорема Эйлера:

В любом выпуклом многограннике сумма числа граней и числа вершин больше числа рёбер на 2.

f + e – k =2

f- число граней;

е – число вершин;

k – число рёбер.

Например, для пирамиды (см. рисунок) :

f = 5- число граней;

e = 5– число вершин;

k = 8– число рёбер.

Проверка:

5+5-8=2 -верно

Призма

Многогранник, составленный из двух равных многоугольников, расположенных в параллельных плоскостях и n параллелограммов, называется призмой.

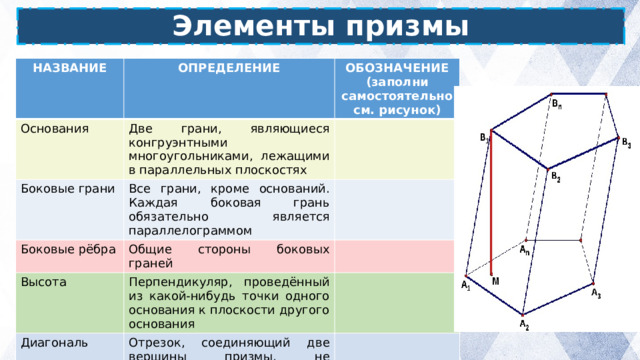
Элементы призмы

НАЗВАНИЕ

ОПРЕДЕЛЕНИЕ

Основания

ОБОЗНАЧЕНИЕ (заполни самостоятельно см. рисунок)

Две грани, являющиеся конгруэнтными многоугольниками, лежащими в параллельных плоскостях

Боковые грани

Все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом

Боковые рёбра

Общие стороны боковых граней

Высота

Перпендикуляр, проведённый из какой-нибудь точки одного основания к плоскости другого основания

Диагональ

Отрезок, соединяющий две вершины призмы, не принадлежащие одной грани

Виды призмы

Перпендикулярны ли боковые рёбра основанию ?

ДА

НЕТ

ПРЯМАЯ ПРИЗМА

НАКЛОННАЯ ПРИЗМА

Прямая призма

Правильный многоугольник лежит в основании?

НЕТ

ДА

ПРАВИЛЬНАЯ ПРИЗМА

ПРЯМОУГОЛЬНЫЙ ПАРАЛЛЕЛЕПИПЕД

ПРЯМОЙ ПАРАЛЛЕЛЕПИПЕД

Площадью полной поверхности призмы называется сумма площадей всех граней (т.е. оснований и боковых граней).

Sполн = 2Sосн + Sбок

Площадь боковой поверхности призмы равна произведению периметра основания на высоту призмы.

Sбок = Ph

Пирамида

Многогранник, составленный из n –угольника и n треугольников, называется пирамидой.

Треугольная пирамида –

Тетраэдр

Четырехугольная пирамида

Шестиугольная пирамида

Элементы пирамиды

Площадью полной поверхности пирамиды называется сумма площадей всех граней (т.е. основания и боковых граней).

Sполн = Sосн + Sбок

Площадью боковой поверхности пирамиды называется сумма площадей её боковых граней.

Правильная пирамида

Пирамида называется правильной , если её основание – правильный многоугольник, а отрезок, соединяющий вершину пирамиды с центром основания, является её высотой

Площадью боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему

Sбок =

P – периметр основания,

h = РМ - апофема

Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется АПОФЕМОЙ

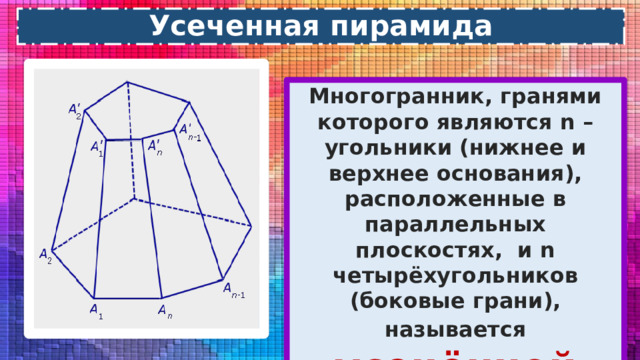
Усеченная пирамида

Многогранник, гранями которого являются n –угольники (нижнее и верхнее основания), расположенные в параллельных плоскостях, и n четырёхугольников (боковые грани), называется усечённой пирамидой.

Усеченная пирамида

Перпендикуляр, проведенный из какой – нибудь точки одного основания к плоскости другого основания, называется высотой усечённой пирамиды

Отрезки А 1 В 1, А 2 В 2, ….. A n B n называются боковыми рёбрами усечённой пирамиды

Боковые грани усечённой пирамиды- трапеции

Правильная усеченная пирамида

Усеченная пирамида называется правильной, если она получена сечением правильной пирамиды плоскостью, параллельной основанию

Основания правильной усечённой пирамиды – правильные многоугольники, а боковые грани – равнобедренные трапеции

Площадь боковой поверхности правильной усечённой пирамиды равна произведению полусуммы периметров оснований на апофему

Sбок = ( P 1 + P 2 ) h

Апофема правильной усечённой пирамиды

Благодарю за внимание!