Презентация "Равновозможные события"

• Равновозможные события

Событие называется случайным, если нельзя утверждать, что это событие в данных обстоятельствах непременно произойдет.

Невозможные события - события, которые в данных условиях произойти не могут.

Достоверное событие - это событие, которое при данных условиях обязательно произойдет.

События которые нельзя разделить на более простые , называются элементарными событиями.

Укажите, какие из следующих событий – невозможные, достоверные, случайные, а о каких мы можем сказать, что оно «маловероятно» или «очень вероятно»:

1. Футбольный матч «Спартак» - «Динамо» закончится вничью.

2. Вы выиграете, участвуя в беспроигрышной лотерее.

3. В полночь выпадет снег, а через 24 часа будет светить солнце.

4. Завтра будет контрольная по математике.

5. Вы получите «5» за контрольную работу по математике.

6. 30 февраля будет дождь.

7. Вас изберут президентом США.

8. Вас изберут президентом России.

9. Круглая отличница получит двойку.

10. На день рождения вам подарят живого крокодила.

Пример элементарных событий.

Опыт: подбрасывание одной игральной кости

Пример:

Опыт: подбрасывают две игральные кости.

Элементарные события: (1;1); (1;2)….

(2;1); (2;2)…

Элементарные события: «выпало одно очко», «выпало два очка», «выпало три очка», «выпало четыре очка», «выпало пять очков», «выпало шесть очков».

Элементарным событием при двух бросаниях игральной кости является пара чисел.

Равновозможные элементарные события

Равновозможные элементарные события – это элементарные события шансы которых одинаковы.

Примеры:

1. При бросании одной игральной кости равновозможных элементарных событий 6.

2. При бросании двух игральных костей равновозможных элементарных

событий 36.

Задача:

Равновозможны ли элементарные события «ОРЕЛ» и «РЕШКА» при бросании правильной монеты.

В каждом опыте сумма вероятностей всех элементарных событий равна 1.

Пример:

Рассмотрим случайный эксперимент, в котором три элементарных события: a, b, c. Вероятности этих элементарных событий обозначим P(a), P(b), P(с). Найти сумму вероятностей этих элементарных событий.

Решение:

В данном случае

Р(а)+Р(в)+Р(с)=1

Пример:

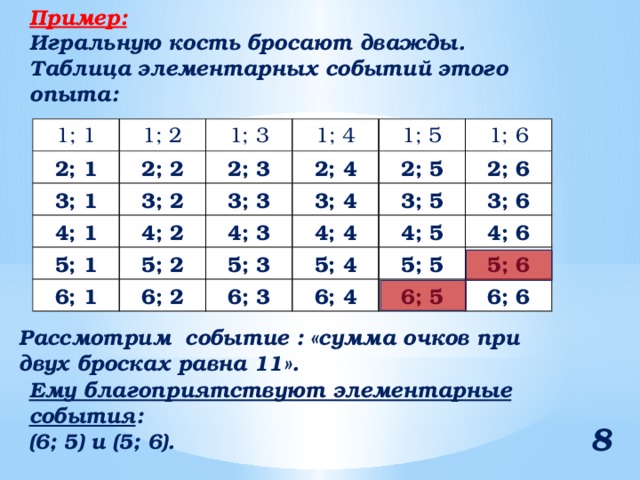
Игральную кость бросают дважды. Таблица элементарных событий этого опыта:

1; 1

1; 2

2; 1

2; 2

3; 1

1; 3

1; 4

4; 1

2; 3

3; 2

4; 2

2; 4

5; 1

3; 3

1; 5

3; 4

6; 1

1; 6

4; 3

2; 5

5; 2

2; 6

6; 2

4; 4

5; 3

3; 5

5; 4

4; 5

6; 3

3; 6

4; 6

6; 4

5; 5

5; 6

6; 5

6; 6

Рассмотрим событие : «сумма очков при двух бросках равна 11».

Ему благоприятствуют элементарные события :

(6; 5) и (5; 6).

8

а) если Р(А)=0, то события называются невозможными;

b) если Р(А)=1, то события называются достоверными;

с) 0 ≤ Р(А) ≤ 1.

9

Вероятности событий

Вероятность события равна сумме вероятностей элементарных событий, благоприятствующих этому событию.

P(A)=P(a)+P(b)+P(с)+P(d) ,

где А-событие,

а, b, c, d – элементарные события, благоприятствующие событию А

10

Пример:

В шахматной партии, которую Остап Бендер играет с любителем шахмат города Васюки, вероятность выигрыша Остапа равна 0,001, вероятность ничьей равна 0,01. Найдем вероятность события А «Остап не проиграл».

Решение:

Благоприятствующие события :

«Остап выиграл»,

«партия окончилась вничью».

P(A) = 0,001 + 0,01 = 0,011

11

Пример:

Автомобиль подъезжает к перекрестку. Вероятность элементарного события «автомобиль свернет вправо» равна 0,5, вероятность элементарного события «автомобиль свернет влево» равна 0,3, вероятность элементарного события «автомобиль поедет прямо» равна 0,18. Нужно найти вероятность события А «автомобиль не поедет обратно».

Решение:

Благоприятствующие события :

«автомобиль свернет вправо»,

«автомобиль свернет влево»,

«автомобиль поедет прямо».

12

P(A) = 0,5 + 0,3 + 0,18 = 0,98

Равновероятные события

События, которые имеют одинаковые вероятности.

13

Пример:

Стрелок один раз стреляет в круглую мишень. При этом вероятность попадания в зоны мишени представлены в таблице:

Зона мишени

1

Вероятность

2

0

3

0,001

0,004

4

5

0,006

0,021

6

7

0,065

8

0,14

9

0,243

10

0,334

0,186

Найдите вероятность события:

а) «стрелок выбил меньше 5 очков»;

б) «стрелок выбил больше 7 очков»;

в) «стрелок попал в черную зону»;

г) «стрелок выбил четное число очков».

Пример:

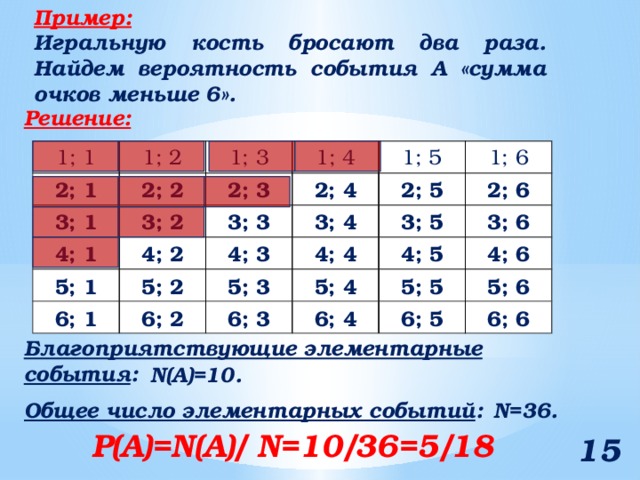
Игральную кость бросают два раза. Найдем вероятность события А «сумма очков меньше 6».

Решение:

Благоприятствующие элементарные события :

1; 1

1; 2

2; 1

2; 2

1; 3

3; 1

3; 2

4; 1

2; 3

1; 4

2; 4

4; 2

3; 3

1; 5

5; 1

6; 1

3; 4

4; 3

1; 6

2; 5

5; 2

2; 6

6; 2

4; 4

3; 5

5; 3

5; 4

4; 5

3; 6

6; 3

6; 4

4; 6

5; 5

5; 6

6; 5

6; 6

N(A)=10.

Общее число элементарных событий :

N=36.

Р(А)=N(A)/ N=10/36=5/18

15

Пример:

Дважды бросают симметричную монету. Найдем вероятность события А «оба раза выпала одна сторона».

Решение:

2

1

О

Р

О

О

Р

О

3

4

Р

Р

О

Р

Благоприятствующие элементарные события :

N(A)=2.

Общее число элементарных событий :

N=4.

Р(А)=N(A)/ N=2/4=1/2

16