Презентация. Теорема Фалеса. 8 класс.

ТЕОРЕМА

ФАЛЕСА

8 класс

МБОУ «Большаковская СОШ» Яковлева Ирина Владимировна

Фалес Милетский VI век до н. э.

Фалес первым сформулировал и доказал несколько геометрических теорем, среди которых:

1) вертикальные углы равны;

2) имеет место равенство треугольников по одной стороне и двум прилегающим к ней углам;

3) углы при основании равнобедренного треугольника равны;

Фалес научился определять расстояние от берега до корабля. В основе этого способа лежит теорема, названная впоследствии теоремой Фалеса:

Е сли параллельные прямые, пересекающие стороны угла, отсекают равные отрезки на одной его стороне, то они отсекают равные отрезки и на другой его стороне.

Легенда рассказывает о том, что Фалес, будучи в Египте, поразил фараона Амасиса тем, что сумел точно установить высоту пирамиды, дождавшись момента, когда длина тени палки становится равной её высоте, и тогда измерил длину тени пирамиды.

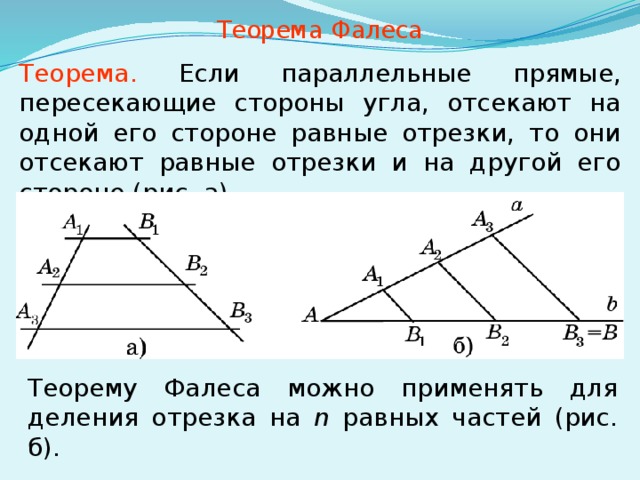
Теорема Фалеса

Теорема. Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне (рис. а).

В режиме слайдов ответы появляются после кликанья мышкой

Теорему Фалеса можно применять для деления отрезка на n равных частей (рис. б).

Теорема о пропорциональных отрезках

Отношением двух отрезков AB и CD называется число, показывающее сколько раз отрезок CD и его части укладываются в отрезке АВ .

Говорят, что отрезки АВ , CD пропорциональны отрезкам A 1 B 1 , C 1 D 1 , если равны их отношения

Теорема. (О пропорциональных отрезках.) Параллельные прямые, пересекающие стороны угла, отсекают от сторон угла пропорциональные отрезки.

В режиме слайдов ответы появляются после кликанья мышкой

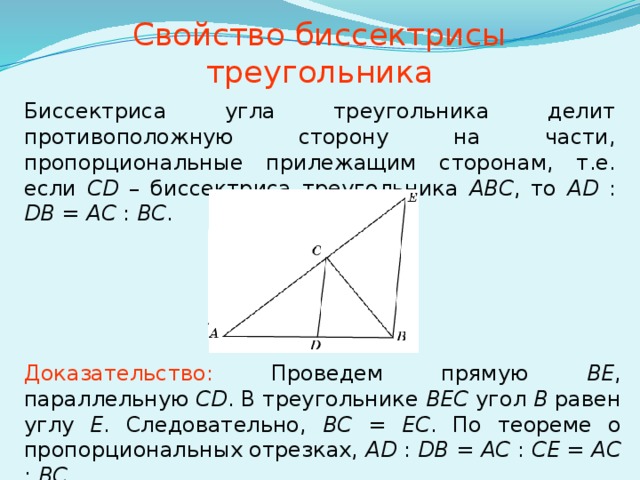
Свойство биссектрисы треугольника

Б иссектриса угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам, т.е. если CD – биссектриса треугольника ABC , то AD : DB = AC : BC .

В режиме слайдов ответы появляются после кликанья мышкой

Доказательство: Проведем прямую BE , параллельную CD . В треугольнике BEC угол B равен углу E . Следовательно, BC = EC . По теореме о пропорциональных отрезках, AD : DB = AC : CE = AC : BC .

5

Обратное свойство

Е сли луч, проведенный из вершины угла треугольника, делит противоположную сторону на части, пропорциональные сторонам треугольника, прилежащим к лучу, то этот луч является биссектрисой угла треугольника.

Доказательство: Пусть для луча CD выполняется равенство AD : DB = AC : BC . Проведем прямую BE , параллельную CD . По теореме о пропорциональных отрезках, AD : DB = AC : CE . Сравнивая эти два равенства, получаем равенство BC = CE , из которого следует равенство углов CBE и BEC . Но угол CBE равен углу BCD , а угол BEC равен углу ACD . Значит, CD – биссектриса треугольника ABC .

В режиме слайдов ответы появляются после кликанья мышкой

5

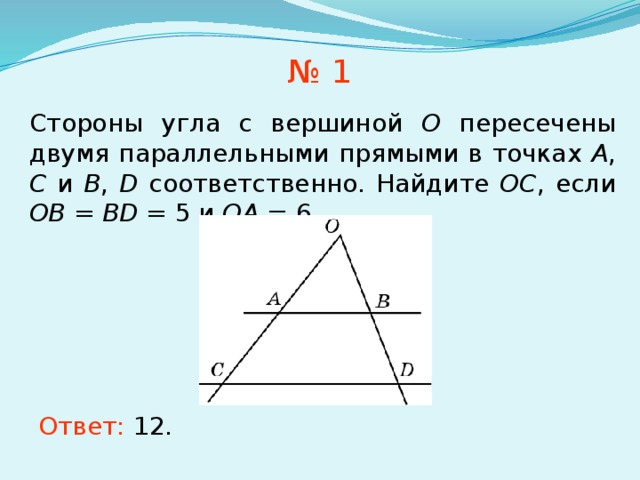
№ 1

Стороны угла с вершиной O пересечены двумя параллельными прямыми в точках A , C и B , D соответственно. Найдите OC , если OB = BD = 5 и OA = 6.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 12.

5

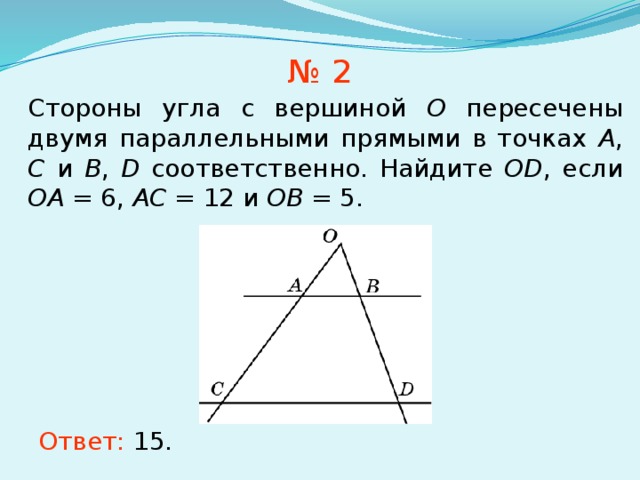
№ 2

Стороны угла с вершиной O пересечены двумя параллельными прямыми в точках A , C и B , D соответственно. Найдите OD , если OA = 6, AC = 12 и OB = 5.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 15.

5

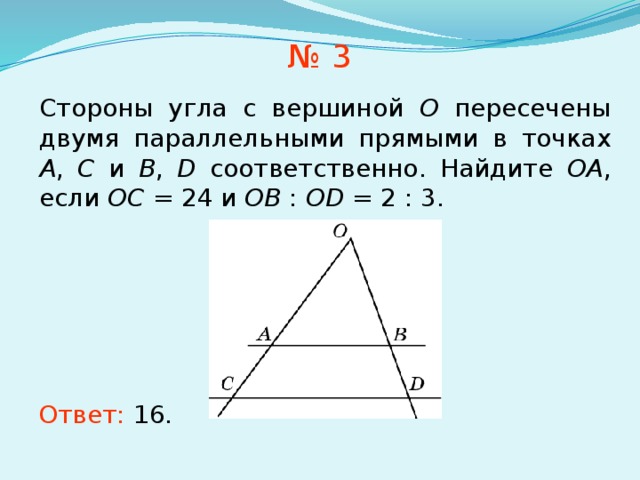
№ 3

Стороны угла с вершиной O пересечены двумя параллельными прямыми в точках A , C и B , D соответственно. Найдите OA , если OC = 24 и OB : OD = 2 : 3.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 16.

5

№ 4

Стороны угла с вершиной O пересечены двумя параллельными прямыми в точках A , B и C , D соответственно. Найдите OA , если OB = 15 см и OC : OD = 2 : 5 .

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 6 см.

5

№ 5

Определите, пропорциональны ли пары отрезков а , b и c , d , если:

а) a = 0,8 см, b = 0,3 см, с = 2,4 см, d = 0,9 см;

б) а = 50 мм, b = 6 см, с = 10 см, d = 18,5 см.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: а) Да;

б) нет.

5

№ 6

Среди отрезков a , b , c , d , e выберите пары пропорциональных отрезков, если а = 2 см, b = 17,5 см, с = 16 см, d = 35 см, е = 4 см.

Ответ: a , e и b , d .

В режиме слайдов ответы появляются после кликанья мышкой

5

Ответ: 8 см.

№ 7

Даны три отрезка: а , b , и с . Какова должна быть длина четвертого отрезка d , чтобы из них можно было образовать две пары пропорциональных отрезков, если а = 6 см, b = 3 cм, с = 4 см, и отрезок d больше каждого из этих отрезков.

В режиме слайдов ответы появляются после кликанья мышкой

5

№ 8

На одной из сторон угла расположены два отрезка 3 см и 4 см. Через их концы проведены параллельные прямые, образующие на другой стороне также два отрезка. Больший из отрезков равен 6 см. Чему равен другой отрезок?

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 4,5 см.

5

№ 9

Стороны угла с вершиной O пересечены двумя параллельными прямыми в точках A 1 , A 2 и B 1 , B 2 соответственно. Найдите: а) B 1 B 2 , если OA 1 = 8 см, A 1 A 2 = 4 см, OB 2 = 6 см; б) OB 1 и OB 2 , если OA 1 : OA 2 = 3 : 5 и OB 2 – OB 1 = 8 см; в) OA 1 и OA 2 , если OB 1 : B 1 B 2 = 2 : 3 и OA 1 + OA 2 = 14 см.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: а) 2 см;

б) 12 см и 20 см;

в) 4 см и 10 см .

5

№ 10

В треугольнике АВС сторона ВС разделена на четыре равные части и через полученные точки деления проведены прямые, параллельные стороне АВ , равной 18 см. Найдите отрезки этих прямых, заключенные внутри треугольника.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 4,5 см, 9 см, 13,5 см.

5

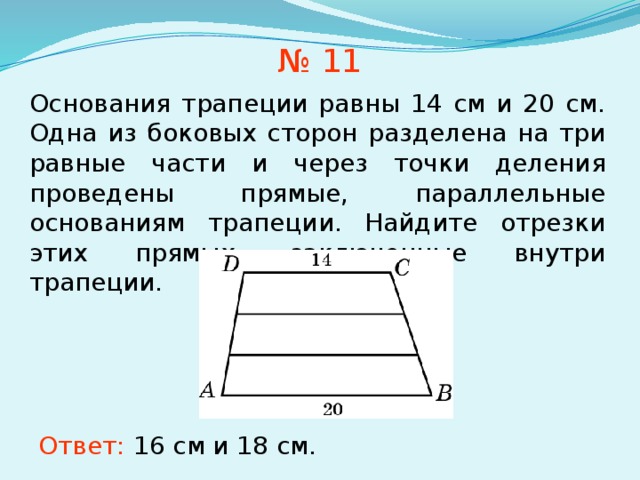
№ 11

Основания трапеции равны 14 см и 20 см. Одна из боковых сторон разделена на три равные части и через точки деления проведены прямые, параллельные основаниям трапеции. Найдите отрезки этих прямых, заключенные внутри трапеции.

В режиме слайдов ответы появляются после кликанья мышкой

Ответ: 16 см и 18 см.

5

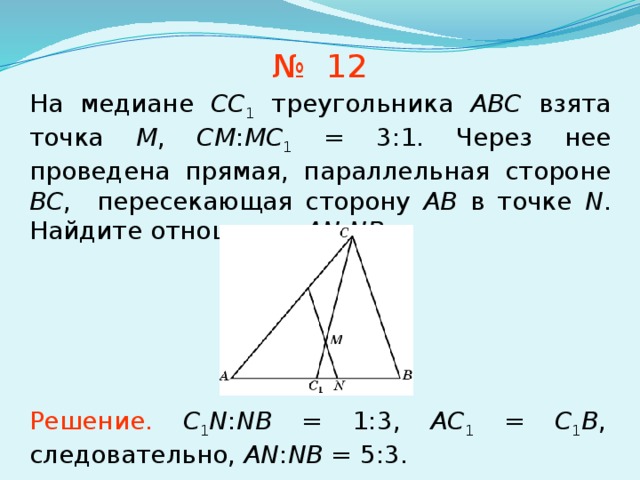
№ 12

На медиане CC 1 треугольника ABC взята точка M , CM : MC 1 = 3:1. Через нее проведена прямая, параллельная стороне BC , пересекающая сторону AB в точке N . Найдите отношение AN : NB .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. C 1 N : NB = 1:3, AC 1 = C 1 B , следовательно, AN : NB = 5:3.

5

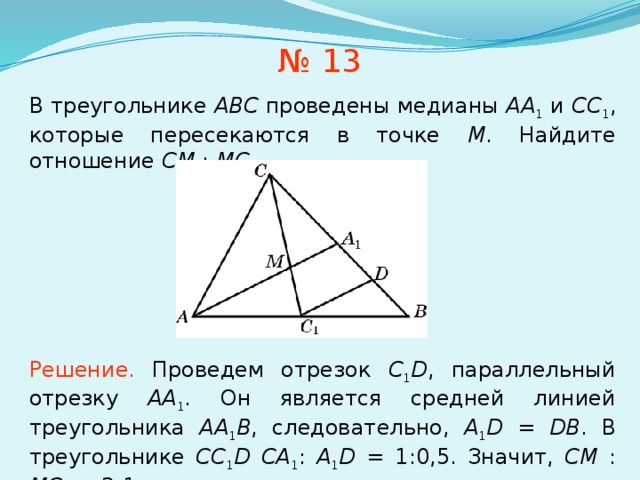
№ 13

В треугольнике ABC проведены медианы AA 1 и CC 1 , которые пересекаются в точке M . Найдите отношение CM : MC 1 .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. Проведем отрезок C 1 D , параллельный отрезку AA 1 . Он является средней линией треугольника AA 1 B , следовательно, A 1 D = DB . В треугольнике CC 1 D CA 1 : A 1 D = 1:0,5. Значит, CM : MC 1 = 2:1.

19

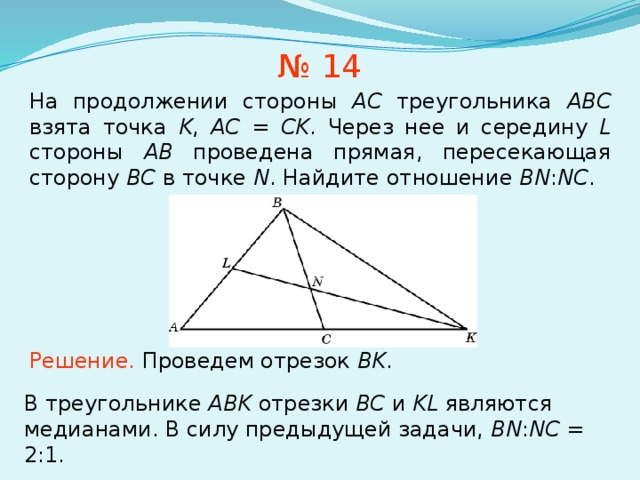
№ 14

На продолжении стороны AC треугольника ABC взята точка K , AC = CK . Через нее и середину L стороны AB проведена прямая, пересекающая сторону BC в точке N . Найдите отношение BN : NC .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. Проведем отрезок BK .

В треугольнике ABK отрезки BC и KL являются медианами. В силу предыдущей задачи, BN : NC = 2:1.

20

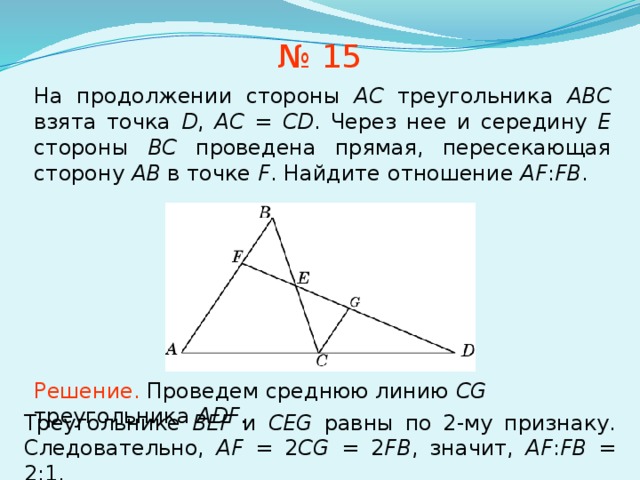
№ 15

На продолжении стороны AC треугольника ABC взята точка D , AC = CD . Через нее и середину E стороны BC проведена прямая, пересекающая сторону AB в точке F . Найдите отношение AF : FB .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. Проведем среднюю линию CG треугольника ADF .

Треугольнике BEF и CEG равны по 2-му признаку. Следовательно, AF = 2 CG = 2 FB , значит, AF : FB = 2:1.

21

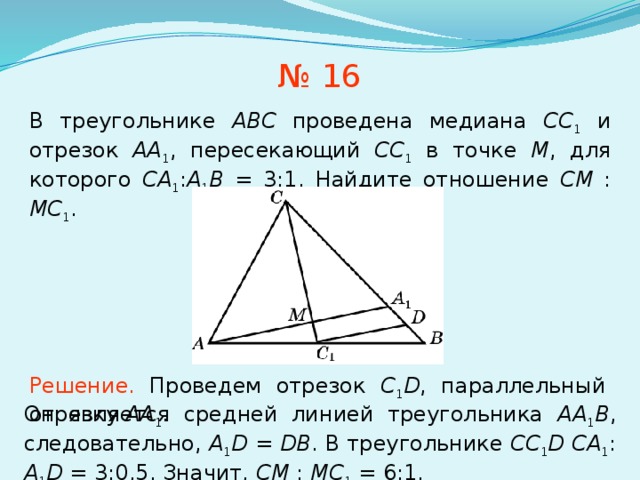
№ 16

В треугольнике ABC проведена медиана СС 1 и отрезок AA 1 , пересекающий CC 1 в точке M , для которого CA 1 : A 1 B = 3:1. Найдите отношение CM : MC 1 .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. Проведем отрезок C 1 D , параллельный отрезку AA 1 .

Он является средней линией треугольника AA 1 B , следовательно, A 1 D = DB . В треугольнике CC 1 D CA 1 : A 1 D = 3:0,5. Значит, CM : MC 1 = 6:1.

22

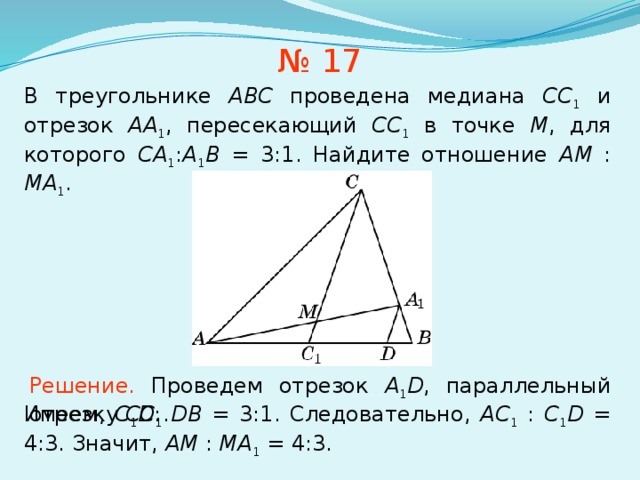
№ 17

В треугольнике ABC проведена медиана СС 1 и отрезок AA 1 , пересекающий CC 1 в точке M , для которого CA 1 : A 1 B = 3:1. Найдите отношение AM : MA 1 .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. Проведем отрезок A 1 D , параллельный отрезку CC 1 .

Имеем, C 1 D : DB = 3:1. Следовательно, AC 1 : C 1 D = 4:3. Значит, AM : MA 1 = 4:3.

23

№ 18

В треугольнике ABC проведена медиана СС 1 и отрезок AA 1 , пересекающий CC 1 в точке M , для которого CA 1 : A 1 B = 1:2. Найдите отношение CM : MC 1 .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. Проведем отрезок C 1 D , параллельный отрезку AA 1 .

Он является средней линией треугольника AA 1 B , следовательно, A 1 D = DB . В треугольнике CC 1 D CA 1 : A 1 D = 1:1. Значит, CM : MC 1 = 1:1.

24

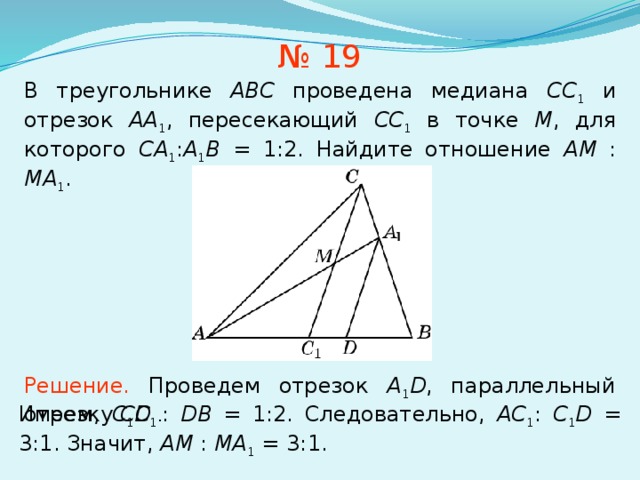
№ 19

В треугольнике ABC проведена медиана СС 1 и отрезок AA 1 , пересекающий CC 1 в точке M , для которого CA 1 : A 1 B = 1:2. Найдите отношение AM : MA 1 .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. Проведем отрезок A 1 D , параллельный отрезку CC 1 .

Имеем, С 1 D : DB = 1:2. Следовательно, AC 1 : C 1 D = 3:1. Значит, AM : MA 1 = 3:1.

25

№ 20

В треугольнике ABC проведена отрезки AA 1 и отрезок CC 1 , пересекающиеся в точке M , для которых AC 1 : C 1 B = 1:2, CA 1 : A 1 B = 2:1. Найдите отношение CM : MC 1 .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. Проведем отрезок C 1 D , параллельный отрезку AA 1 . Тогда A 1 D : DB = AC 1 : C 1 B = 1:2 . В треугольнике CC 1 D CA 1 : A 1 D = 2 : 1/3. Значит, CM : MC 1 = 6:1.

26

№ 21

В треугольнике ABC проведена медиана СС 1 и отрезок AA 1 , пересекающий CC 1 в точке M , для которого CA 1 : A 1 B = 2:1. Найдите отношение AM : MA 1 .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. Проведем отрезок A 1 D , параллельный отрезку CC 1 . Тогда C 1 D : DB = 2:1, AC 1 = C 1 B . Следовательно, AC 1 : C 1 D = 3:2. Значит, AM : MA 1 = 3:2.

27

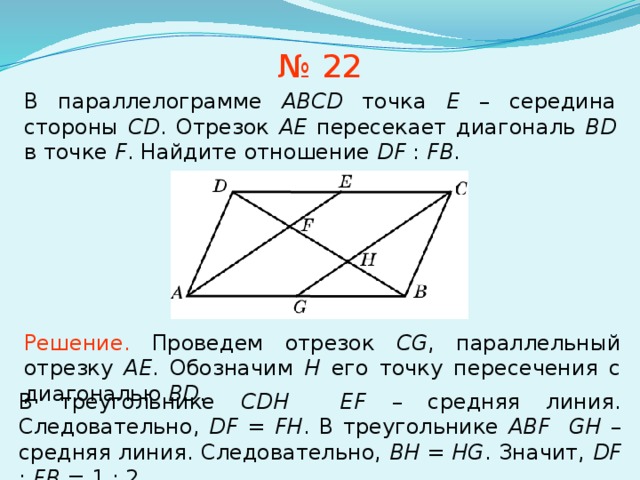
№ 22

В параллелограмме ABCD точка E – середина стороны CD . Отрезок AE пересекает диагональ BD в точке F . Найдите отношение DF : FB .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. Проведем отрезок CG , параллельный отрезку AE . Обозначим H его точку пересечения с диагональю BD .

В треугольнике CDH EF – средняя линия. Следовательно, DF = FH . В треугольнике ABF GH – средняя линия. Следовательно, BH = HG . Значит, DF : FB = 1 : 2.

28

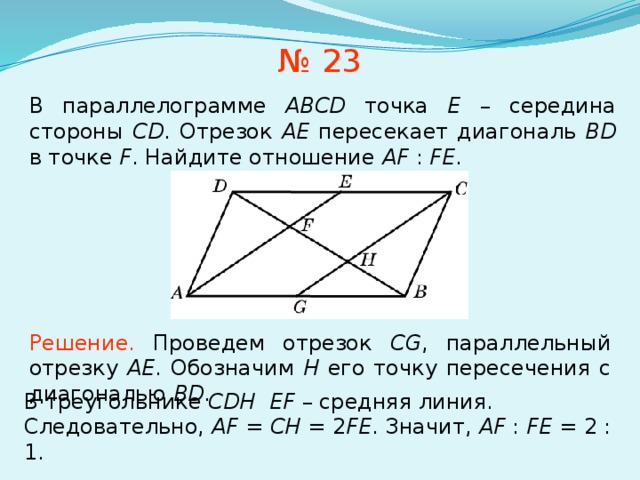
№ 23

В параллелограмме ABCD точка E – середина стороны CD . Отрезок AE пересекает диагональ BD в точке F . Найдите отношение AF : FE .

В режиме слайдов ответы появляются после кликанья мышкой

Решение. Проведем отрезок CG , параллельный отрезку AE . Обозначим H его точку пересечения с диагональю BD .

В треугольнике CDH EF – средняя линия. Следовательно, AF = CH = 2 FE . Значит, AF : FE = 2 : 1.

29

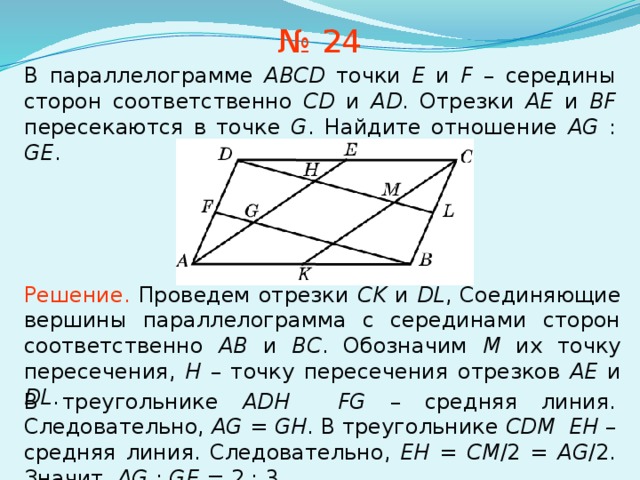
№ 24

В параллелограмме ABCD точки E и F – середины сторон соответственно CD и AD . Отрезки AE и BF пересекаются в точке G . Найдите отношение AG : GE .

Решение. Проведем отрезки CK и DL , Соединяющие вершины параллелограмма с серединами сторон соответственно AB и BC . Обозначим M их точку пересечения, H – точку пересечения отрезков AE и DL .

В режиме слайдов ответы появляются после кликанья мышкой

В треугольнике ADH FG – средняя линия. Следовательно, AG = GH . В треугольнике CDM EH – средняя линия. Следовательно, EH = CM /2 = AG /2. Значит, AG : GE = 2 : 3.

30

Использованы ресурсы: