

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Была в сети 15.05.2025 07:24

Шекера Оксана Александровна
учитель
40 лет
Местоположение
Россия, Новосибирск
Специализация







 Представление графов
Представление графов 
 Алгоритм Дейкстры
Алгоритм Дейкстры  Алгоритм Крускала
Алгоритм Крускала  Находит кратчайшие пути между всеми парами вершин.
Находит кратчайшие пути между всеми парами вершин. Алгоритм Прима
Алгоритм Прима 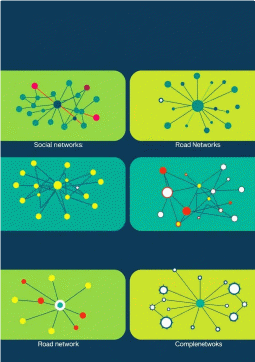
 Социальные сети, сетевые технологии, маршрутизация, транспортные системы, картография, анализ данных, машинное обучение.
Социальные сети, сетевые технологии, маршрутизация, транспортные системы, картография, анализ данных, машинное обучение.














