Презентация "Уравнение окружности и прямой"

Уравнение прямой и окружности

Орехова Ольга Юрьевна, учитель математики и информатики

ГКОУ СО «Екатеринбургская вечерняя школа №1»

Уравнение фигуры –

это уравнение

с двумя переменными х и у , которому удовлетворяют координаты любой точки фигуры.

Каноническое уравнение прямых

На координатной плоскости прямая - это график линейной функции, которая задана уравнением вида :

Рассмотрим следующее уравнение прямой:

Каноническая запись

Каноническое уравнение прямых

В общем виде :

В канонической записи уравнения прямых принято использовать целые коэффициенты.

Выполним обратную операцию :

у = -2х - 3

Задание

Постройте на координатной плоскости множества точек, соответствующих уравнениям:

3

1

2

Уравнение окружности

( х – а ) 2 + ( у – b ) 2 = R 2

уравнение окружности, где

А ( а ; b ) − центр, R − радиус,

х и у – координаты точки окружности .

Если А (5;5) – центр, R = 3 , то

( х – 5 ) 2 + ( у – 5 = 3 2 ;

( х – 5 ) 2 + ( у – 5 ) 2 = 9 .

Уравнение окружности

( х – а ) 2 + ( у – b ) 2 = R 2 .

Центр окружности О (0;0 ),

( х – 0 ) 2 + ( у – 0 ) 2 = R 2 ,

х 2 + у 2 = R 2 − уравнение

окружности с центром в

начале координат. .

О (0;0) – центр, R = 5, х 2 + у 2 = 5 2 ;

х 2 + у 2 = 25 .

Для того чтобы составить уравнение окружности, нужно:

1) узнать координаты центра;

2) узнать длину радиуса;

3) подставить координаты центра ( а ; b )

и длину радиуса R

в уравнение окружности

( х – а ) 2 + ( у – b ) 2 = R 2 .

2. Определите является данное уравнение уравнением окружности.Найти координаты центра, радиус и диаметр

№ 1. Составить уравнение окружности.

координаты центра: (0 ; 0)

R = 3

Уравнение окружности:

№ 2. Составить уравнение окружности.

координаты центра:

( 4 ; 0 )

R = 3

уравнение окружности:

№ 3. Составить уравнение окружности.

координаты центра:

(- 4 ; 4 )

R = 2

уравнение окружности:

№ 4. Составить уравнение окружности.

координаты центра:

(- 3 ; 4 )

R = 4

уравнение окружности:

№ 5 Заполните таблицу .

№

Уравнение окружности

1

( х – 5) 2 + ( у + 3) 2 = 36

Радиус

2

3

Коорд . центра

R=

( х – 1) 2 + ( у + 1) 2 = 2

( х + 1) 2 + ( у – 7) 2 = 49

( ; )

4

R=

( ; )

R=

х 2 + у 2 = 81

5

( ; )

( у – 5) 2 + ( х + 3) 2 = 7

6

R=

( х + 3) 2 + у 2 = 14

( ; )

R=

( ; )

R=

( ; )

№ 6. Постройте в тетради окружности, заданные уравнениями:

• ( х – 5) 2 + ( у + 3) 2 = 36;

2 ) ( х + 1) 2 + ( у – 7) 2 = 49.

Самостоятельная работа

Проверка

1а) 0,5 1б) 0,5 1в) 1 2) 1 3) 1 4) 1

2 вариант

1 вариант

1.a) (4;-2)

1.б) r = 3

1.в) (х-4)²+(y+2)²=9

1.а) (-4;2)

1.б) r = 4

1.в) (х+4)²+(y-2)²=16

2. (x+1)²+(y-3)²=36

2. (x-2)²+(y+4)²=9

3. В- да А- нет

3. В- нет А- да

4. r = 5

4. r = 13

Спасибо за внимание!

Группа2: №1 Найдите координаты центра и радиус, если АВ – диаметр данной окружности.

Дано

Радиус

А (0;−6)

Координаты центра

В (0; 2)

d 2 = ( x 2 – x 1 ) 2 + ( y 2 – y 1 ) 2

А (−2;0)

СВ 2 = R 2 =

В ( 4; 0)

А (0; −6)

R 2 =

В (0; 2) .

R =

С ( ; )-середина АВ

С ( ; )

№ 2

• Построить по полученным данным окружности в тетради.
• Составить алгоритм построения окружности по координатам концов диаметра

Вернуться к групповым заданиям

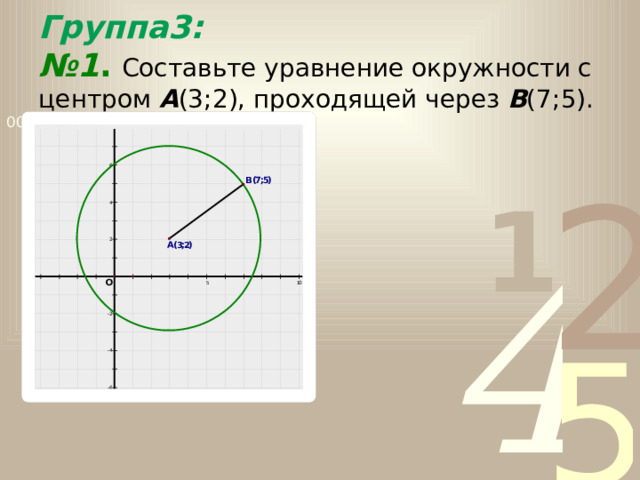
Группа3: №1 . Составьте уравнение окружности с центром А (3;2), проходящей через В (7;5).

№ 2 . Составьте уравнение окружности с центром в точке С (3;−1), проходящей через начало координат.

Вернуться к групповым заданиям