Приемы устного счета

Приемы быстрого счета

Выполнила :

ученица 7Б класса школы №168

Руководитель проекта :

Чистякова Т.В.

2017 год

Цель проекта :

• изучить методы и приемы быстрого счета
• и показать необходимость их эффективного использования.

Гипотеза исследования :

• Если показать, что применение приемов быстрого счета, облегчает вычисления, то можно добиться того, что повысится вычислительная культура учащихся, и им будет легче решать практические задачи.
• Объект исследования: различные алгоритмы счета
• Предмет исследования: процесс вычислений.
• Субъект исследования: учащиеся 7 класса.

Задачи проекта :

• изучить историю возникновения вычислений
• рассмотреть правила вычислений, которыми пользовались в древности и которыми пользуются сейчас,
• освоить правила быстрого счета и научиться пользоваться ими

История возникновения вычислений

Вот как они выглядели:

СПОСОБЫ ЗАПИСИ ЧИСЕЛ

Этот способ обозначения цифр называется цифирью:

СИСТЕМЫ СЧИСЛЕНИЯ

.2

:2

47 35

23 70

11 140

5 280

2 560

1 1120

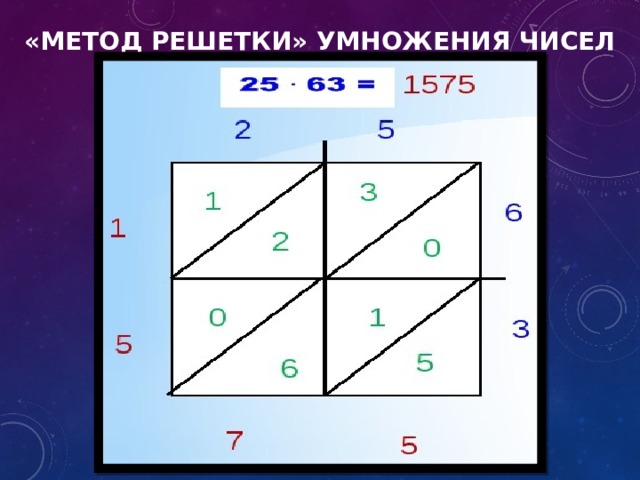
«Метод решетки» умножения чисел

Египетский способ умножения

Заменить умножение на любое число - удвоением, то есть сложением числа с самим собой.

Пример:

34 ∙ 5 = 34∙ (1 + 4) =

= 34 ∙ 1+ 34 ∙ 4.

Т. к. 5 = 4 + 1, то для получения ответа оставалось сложить числа, стоящие в правом столбике против цифр 4 и 1 , т. е.

136 + 34 = 170.

Яков Трахтенберг- еврейско-русский математик, который, находясь в заключении в фашистском концлагере во время Второй мировой войны, разработал систему быстрого счета. Занимался он этим, чтобы сохранить рассудок. Система Трахтенберга позволяет умножать большие числа на небольшие.

Метод Якова Трахтенберга

Яков Трахтенберг ушел из жизни в 1953 году. Сведений об этом замечательном человеке сохранилось обидно мало. Что же касается его замечательного изобретения, то к нему вполне применим, не утративший своей актуальности, античный афоризм: “Не знающие пусть научатся, а знающие вспомнят ещё раз”.

Умножение на 11 по Трахтенбергу

Правило: Добавь цифру к её соседу.

(Под  соседом  подразумевается цифра справа.)

Пример: 3,425 × 11 = 37,675

0,3425 × 11 = (0+3), (3+4)(4+2)(2+5)(5+0) = 3,7675

Доказательство:

11 = 10+1

Таким образом:

3425 x 11 = 3425 x(10+1) = 34250 + 3425 = 37675

Результаты эксперимента до изучения методов:

Результаты эксперимента после изучения методов:

Вывод

Гипотеза подтвердилась:

Когда мы показали, что применение приемов быстрого счета, облегчает вычисления, то ы добились того, что вычислительная культура учащихся повысилась, и им стало легче решать практические задачи.

Цель достигнута:

В результате практического и теоретического исследования мы изучили приёмы быстрого счёта, а так же научили приёмам быстрого счёта учащихся нашего класса .

Спасибо за внимание!