Просмотр содержимого документа
«Презентация к уроку "Осевая и центральная симметрия"»

Кудря Елена Николаевна
МБОУ СОШ № 7 посёлка Северного


“ Симметрия является той идеей, посредством которой человек на протяжении веков пытался постичь и создать порядок, красоту и совершенство”.
Г. Вейль

Устная работа!
-20
1) 5∙(-2)+(-2)∙5=
2) 24:(-8)+(-8):24=
3) 12∙(-3)-(-3)∙12=
0
4)
4
5)
12
6)
69

№ 1200 (№ 913)
№ 1206 (№ 919)
А 1 (-2;-5), В 1 (-4;-1).
А 1 (7;-1), В 1 (2;-7), С 1 (3;-1).

Проверочный тест

- Если при сгибании плоскости чертежа по прямой, две фигуры совместятся, то такие фигуры называются симметричными относительно прямой.
- Если фигура некоторой прямой делится на две симметричные части, то ее называют симметричной относительно этой прямой. Прямая, относительно которой симметричны части фигуры, называются осью симметрии.
- Луч, который выходит из вершины угла и делит его пополам, называется биссектрисой угла.
- Прямоугольник имеет 2 оси симметрии.
- Квадрат имеет 4 оси симметрии.
- Окружность имеет бесконечное множество осей симметрии.
- Фигура называется центрально-симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.
- Окружность - центрально-симметричная фигура.
- Отрезок - центрально-симметричная фигура.
- Прямоугольник - центрально-симметричная фигура.
- На координатной плоскости координаты точек, симметричных относительно точки О – начало координат, являются противоположными числами .

- Если при сгибании плоскости чертежа по прямой, две фигуры совместятся, то такие фигуры называются симметричными относительно прямой.
- Если фигура некоторой прямой делится на две симметричные части, то ее называют симметричной относительно этой прямой. Прямая, относительно которой симметричны части фигуры, называются осью симметрии.
- Луч, который выходит из вершины угла и делит его пополам, называется биссектрисой угла .
- Прямоугольник имеет 2 оси симметрии.
- Квадрат имеет 4 оси симметрии.
- Окружность имеет бесконечное множество осей симметрии.
- Фигура называется центрально-симметричной относительно точки О, если для каждой точки фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.
- Окружность - центрально-симметричная фигура.
- Отрезок - центрально-симметричная фигура.
- Прямоугольник - центрально-симметричная фигура.
- На координатной плоскости координаты точек, симметричных относительно точки О – начало координат, являются противоположными числами .

11 баллов – «5»
10-9 баллов - «4»
8-6 баллов – «3»
5-0 баллов – «2»

Симметрия
Симметрия в переводе с греческого- « summetria » соразмерность, пропорциональность, наличие определенного порядка в расположении частей.

Примеры симметричных фигур

Равнобедренный
треугольник
Равнобедренная трапеция
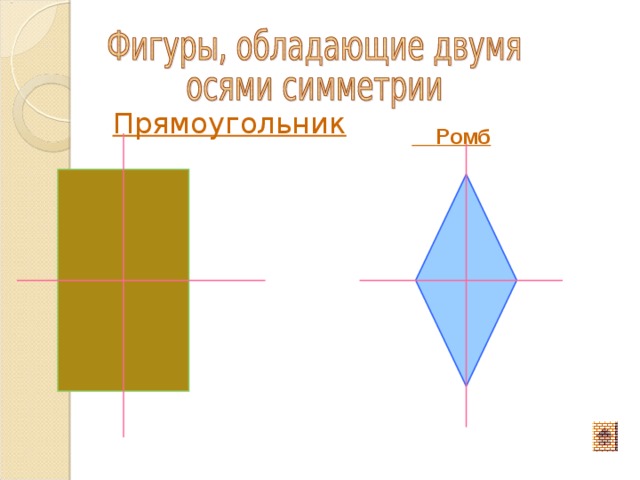
Прямоугольник
Ромб
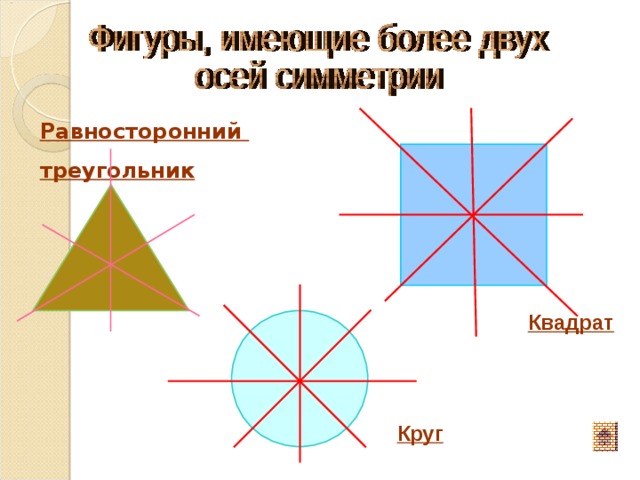
Равносторонний
треугольник
Квадрат
Круг

Найдите лишнюю фигуру
Какая из фигур, приведенных на рисунке, лишняя?
- Фигура 1
- Фигура 2
- Фигура 3
- Фигура 4
- Фигура 5

Перейти к слайду Симметрия в природе

Ты не угадал!
Не отчаивайся!
Попробуй еще раз!

12









Байтерек.

Финляндия. Православный храм

Государственный Эрмитаж. Санкт – Петербург. Петровский зал .

Петергоф. Павильон Оранжерея.

… В гранит оделася Не ва ;
Мосты повисли над во дами ;
------------------------------------------------
Темно-зелеными са дами
Ее покрылись остро ва …
Пушкин А.С. «Медный всадник»

- В переводе с греческого – «бегущий обратно, возвращающийся»
- История палиндрома восходит к глубокой древности, прежде всего античности
- Впервые появились на амфорах, вазах и других предметах сферической формы.

палиндром
перевертень
перевертыш
Справа налево и
слева направо
ВОР БОБРОВ !
НЕСУН ГНУСЕН !

Стихотворные палиндромы называли рачьими стихами.
Афанасий Фет придумал выражение
А РОЗА УПАЛА НА ЛАПУ АЗОРА
- Велемир Хлебников прославился тем, что написал целую палиндром - поэму в 400 строк.

“ ИСКАТЬ ТАКСИ”,
“ АРГЕНТИНА МАНИТ НЕГРА”,
“ ЦЕНИТ НЕГРА АРГЕНТИНЕЦ”,
ШОРОХ ХОРОШ.

Буквы и слова
Некоторые буквы и слова имеют ось симметрии!
Вертикальную: Горизонтальную:
А О П Ж Т Ф М Х Н Ш В О З С К Х Е Н Э Ю



Заключение
Симметрию можно обнаружить почти везде, если знать, как ее искать. Многие народы с древнейших времен владели представлением о симметрии в широком смысле – как об уравновешенности и гармонии. Творчество людей во всех своих проявлениях тяготеет к симметрии. Посредством симметрии человек всегда пытался, по словам немецкого математика Германа Вейля, «постичь и создать порядок, красоту и совершенство».


























































