Презентация по теме: "Движения".

Темы презентации :

• Движение. Преобразования фигур.

Симметрия относительно точки.

Симметрия относительно прямой.

Поворот. Параллельный перенос.

2. Векторы. Сложение, вычитание векторов.

Умножение вектора на число. Решение

задач.

Слайды № 9,11, 13, 16, 17 демонстрируют творческие работы

учащихся по заданным темам.

Выполнила студентка группы 13/14

Груздева Анастасия.

Уроки геометрии в 8 классе

А

С

В

Преобразование одной фигуры в другую, при котором

сохраняется расстояние между точками называется

движением.

. А

. А

Точки, лежащие на прямой, при движении переходят

в точки, лежащие на прямой, и сохраняется порядок

их взаимного расположения.

В

А

В

С

С

А

Следовательно: при движении

прямые переходят в прямые,

полупрямые – в полупрямые,

отрезки – в отрезки,

сохраняются углы между полупрямыми.

Центральная

симметрия

Осевая симметрия

Поворот

Параллельный

перенос

А

О

В

О

Точка А симметрична точке В относительно

центра симметрии – точки О

а

n

А

В

Точка А симметрична

точке В относительно

прямой а – оси симметрии

А

О

Х

В

О – центр поворота

угол АОВ – угол поворота

направление поворота –

по часовой стрелке

О

Направление поворота –

по часовой стрелке

Параллельный перенос задается формулами

Преобразование фигуры F , при котором ее произвольная точка ( х; у) переходит в точку ( х+а; у+в) называется параллельным переносом.

Задается формулами

В какие точки при этом параллельном

переносе переходят точки О(0;0), А(0;4),

В(-4;1)?

Параллельный перенос определяется как

преобразование, при котором точки

смещаются в одном и том же направлении

на одно и то же расстояние.

Р

О

В

А

Направленный отрезок ОР

задает

параллельный перенос

Лучи АВ и ОР одинаково направлены

АВ = ОР

Композиция движений

В

М

Р

С

Т

А

О

Вектор – направленный

отрезок.

Вектор АВ обозначается

Н

К

Назовите векторы,

начало и конец

вектора.

Точка А – начало вектора,

точка В – конец вектора.

Д

- противоположно

направленные

векторы

- одинаково направленные

векторы

• абсолютная величина

(или модуль) вектора – это

длина отрезка, изображающего вектор

Назовите одинаково направленные и противоположно направленные векторы

=

Равные векторы одинаково

направлены и равны по

абсолютной величине

Как от точки отложить вектор, равный

данному?

=

А

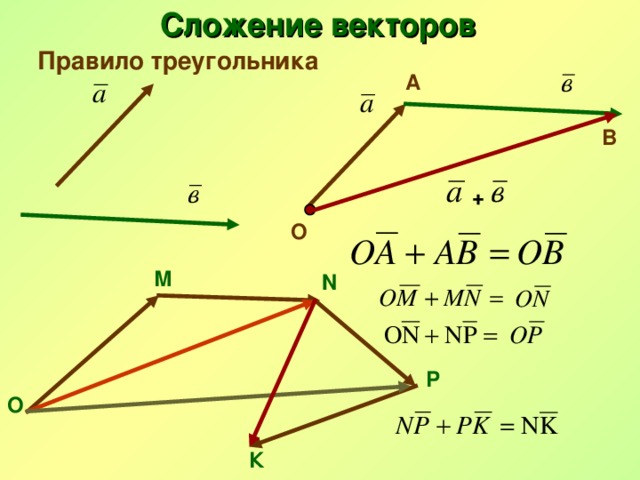
Сложение векторов

Правило треугольника

А

В

+

О

М

N

Р

О

К

Правило параллелограмма

К

О

Р

Т

М

К

А

В

С

Д

Постройте векторы:

H

K

F

L

N

P

O

M

U

T

S

R

А

В

С

Д

Постройте векторы:

H

K

F

L

N

P

O

M

U

T

S

R

Вычитание векторов

А

О

В

Как проверить?

А

В

С

Д

Постройте векторы:

H

K

F

L

O

P

N

M

U

T

S

R

Умножение вектора на число

О

К

сонаправленные, если

и

противоположно направленные, если

От точки N отложите

векторы

N