Презентация "Теорема Фалеса"

Теорема Фалеса

Геометрия

8 класс

Устный счет Найдите углы параллелограмма

В

С

?

?

В

С

?

107 °

?

64 °

D

А

?

?

А

D

Устный счет Найдите углы трапеции

В

С

?

107 °

?

45 °

D

А

В

С

?

?

32 °

74 °

А

D

Устный счет Найдите углы равнобедренной трапеции

В

С

?

?

В

С

?

101 °

?

47 °

А

D

?

?

D

А

Устный счет Найдите периметр параллелограмма

25 см

15 см

12 см

2,8 дм

Фалес Милетский

Древнегреческий философ, родоначальник античной и вообще европейской философии и науки, основатель милетской школы.

Важнейшей заслугой Фалеса в области математики считается перенесение им из Египта в Грецию первых начал теоретической элементарной геометрии:

• вертикальные углы равны;
• углы при основании равнобедренного треугольника равны;
• треугольник определяется стороной и прилежащими к ней двумя углами;
• диаметр делит круг на две равные части .

Фалесу приписывается решение двух геометрических задач практического характера: определение расстояния на море от корабля до Милетской гавани и определение высоты пирамиды по длине ее тени.

В

М

N

Задача . Через середину М стороны треугольника АВС проведена прямая, параллельная стороне АС. Эта прямая пересекает сторону ВС в точке N. Докажите, что ВN=NС.

А

С

Задача . Через середину М стороны треугольника АВС проведена прямая, параллельная стороне АС. Эта прямая пересекает сторону ВС в точке N. Докажите, что ВN=NС.

Доказательство : Через точку С проведем СD ║АВ.

АМ = МВ – по условию, АМ = СD по построению (АМDС – параллелограмм). Значит МВ = СD,

ВМN = CDN

ВN = NС.

В

3

D

N

М

1

2

4

С

А

Теорема Фалеса . Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их вершины провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки .

А1А2=А2А 3 =А 3 А 4 =… В1В2 ? В2В 3 ? В 3 В 4 ?...

Доказательство :

Через точку В1 проведем . А1А2 = В1С,

А2А1В1С – параллелограмм.

А2А 3 = СD,

А3А2СD – параллелограмм.

Т. к. А1А2 = А2А 3 , то В1С = СD.

В треугольнике В1DВ 3

В1С = СD и СВ2 DВ 3

Значит В1В2 = В2В 3 .

Аналогично можно доказать, что В2В 3 = В 3 В 4 = …

Теорема Фалеса до сих пор используется в морской навигации в качестве правила о том, что столкновение судов, двигающихся с постоянной скоростью, неизбежно, если сохранять курс судов друг на друга .

Решение задач по готовым чертежам А 1 В 1 ‖А 2 В 2 ‖А 3 В 3 ‖А 4 В 4 ; АА 1 =А 1 А 2 =А 2 А 3 =А 3 А 4 ; АВ 4 =20 см. Найти В 2 В 3.

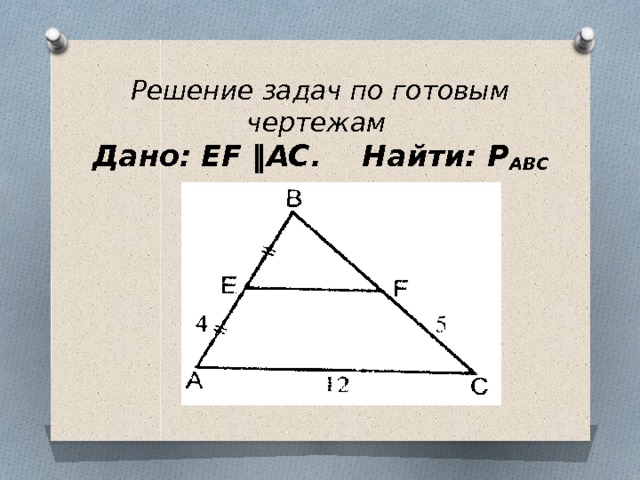
Решение задач по готовым чертежам Дано: EF ‖AC. Найти: Р АВС

Решение задач по готовым чертежам ABCD – трапеция. Доказать: АО = ОС.

Решение задач по готовым чертежам ABCD – трапеция, МК ‖ ВЕ ‖ СD, АD = 16. Найти: АК.