Презентация "Трапеция"

ТРАПЕЦИЯ

Меркулова Е.И.,

учитель математики

МБОУ Мало-Вязёмская СОШ

2016

Трапеция

Трапеция (от греч. trapеzion — четырёхугольник с неравными сторонами, буквально — столик), выпуклый четырёхугольник, у которого две стороны параллельны, а две другие — непараллельны .

Параллельные стороны называются основаниями трапеции, а непараллельные - её боковыми сторонами .

Формула площади трапеции:

Площадь геометрической фигуры - часть поверхности, ограниченная замкнутым контуром данной фигуры. Величина площади трапеции выражается числом заключающихся в него квадратных единиц.

Площадь трапеции равна произведению полусуммы ее оснований на высоту (a, b, h)

S - площадь трапеции

a - длина 1-ого основания

b - длина 2-ого основания

h - длина высоты трапеции

Формула периметра трапеции:

Периметр геометрической фигуры - суммарная длина границ плоской геометрической фигуры. Периметр имеет ту же размерность величин, что и длина.

Периметр трапеции равен сумме 4-х её сторон (a, b, c, d).

P - периметр трапеции

a, c - длины оснований трапеции

b, d - длины боковых сторон трапеции

Виды трапеций:

Трапеция, у которой боковые стороны не равны, называется

РАЗНОСТОРОННЕЙ

Трапеция, у которой боковые стороны равны, называется РАВНОБЕДРЕННОЙ

Трапеция, у которой одна боковая сторона составляет прямой угол с основаниями, называется ПРЯМОУГОЛЬНОЙ

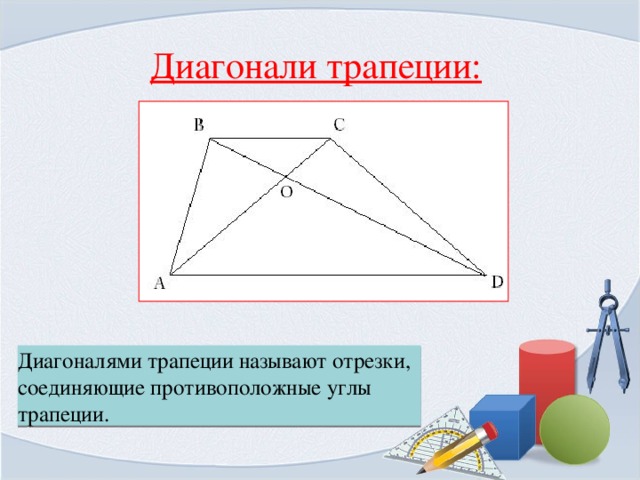
Диагонали трапеции:

Диагоналями трапеции называют отрезки, соединяющие противоположные углы трапеции.

Высота трапеции:

Высотой трапеции называют перпендикуляр, опущенный из любой точки одного оснований трапеции на другое основание или его продолжение

Средняя линия трапеции:

Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции

Средняя линия трапеции:

a   - нижнее основание

b   - верхнее основание

m   - средняя линия

Свойство (точка пересечения диагоналей)

Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой

Свойство (биссектрисы углов при боковой стороне)

Биссектрисы углов при боковой стороне трапеции перпендикулярны

СПАСИБО ЗА ВНИМАНИЕ