Презентация "Цилиндр. Сечение цилиндра плоскостью"

« Не делай никогда того, чего не знаешь,

но научись всему, что следует знать»

Пифагор  

10.02.17

10.02.17

Объемные тела. Тела вращения

ЦИЛИНДР

Сечения цилиндра плоскостью

Примеры цилиндров

Слово цилиндр - означает от греческого слова “ валик ”, “ каток ”.

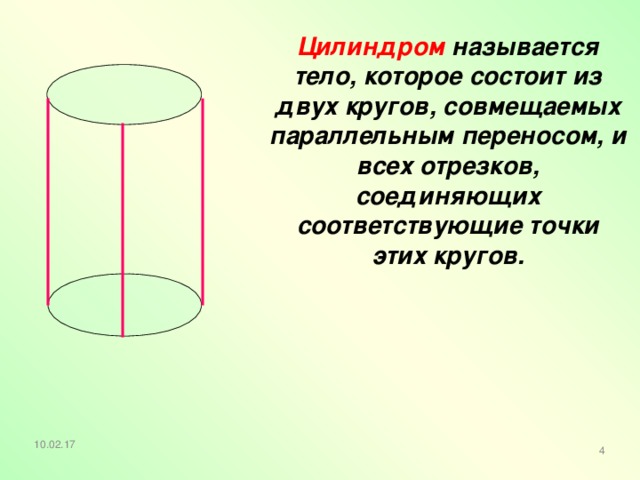
Цилиндром называется тело, которое состоит из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.

10.02.17

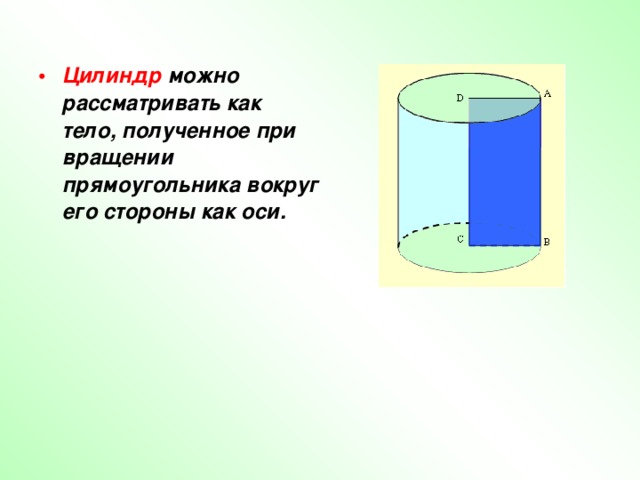
• Цилиндр можно рассматривать как тело, полученное при вращении прямоугольника вокруг его стороны как оси.

Основные определения

Основаниями цилиндра называются круги, полученные в результате вращения сторон прямоугольника, смежных со стороной принадлежащей оси вращения.

Образующими цилиндра называются отрезки, соединяющие соответствующие точки окружностей кругов.

O 1

Н

O

R

Радиусом цилиндра называется радиус его основания.

Высотой цилиндра называется расстояние между плоскостями оснований.

Осью цилиндра называется прямая, проходящая через центры оснований.

10.02.17

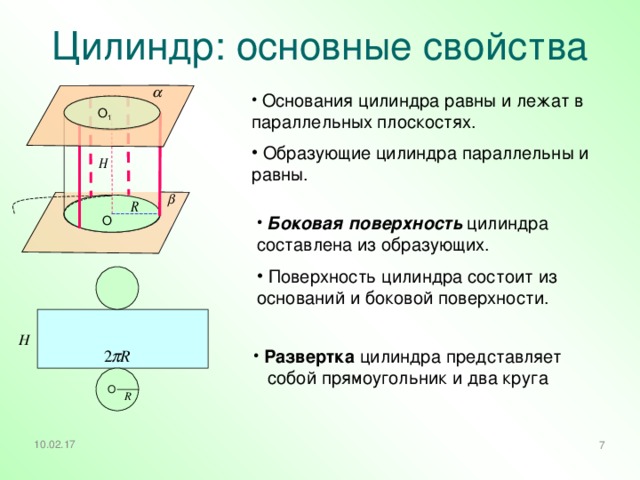
Цилиндр: основные свойства

• Основания цилиндра равны и лежат в параллельных плоскостях.
• Образующие цилиндра параллельны и равны.

O 1

• Боковая поверхность цилиндра составлена из образующих.
• Поверхность цилиндра состоит из оснований и боковой поверхности.

O

• Развертка цилиндра представляет собой прямоугольник и два круга

O

10.02.17

7

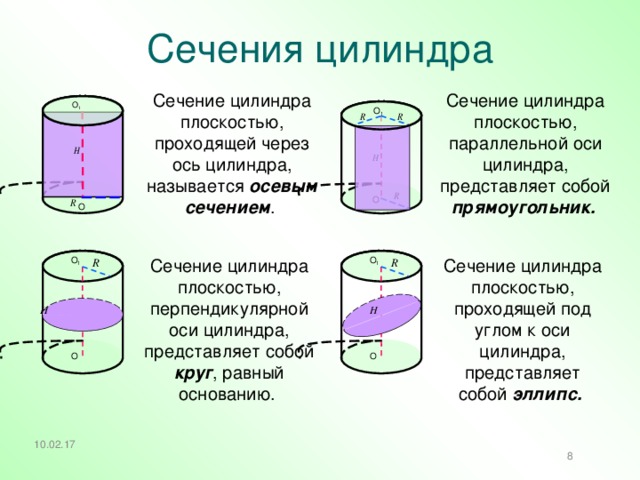
Сечения цилиндра

Сечение цилиндра плоскостью, проходящей через ось цилиндра, называется осевым сечением .

Сечение цилиндра плоскостью, параллельной оси цилиндра, представляет собой прямоугольник.

O 1

O 1

O

O

O 1

O 1

Сечение цилиндра плоскостью, проходящей под углом к оси цилиндра, представляет собой эллипс.

Сечение цилиндра плоскостью, перпендикулярной оси цилиндра, представляет собой круг , равный основанию.

O

O

10.02.17

8

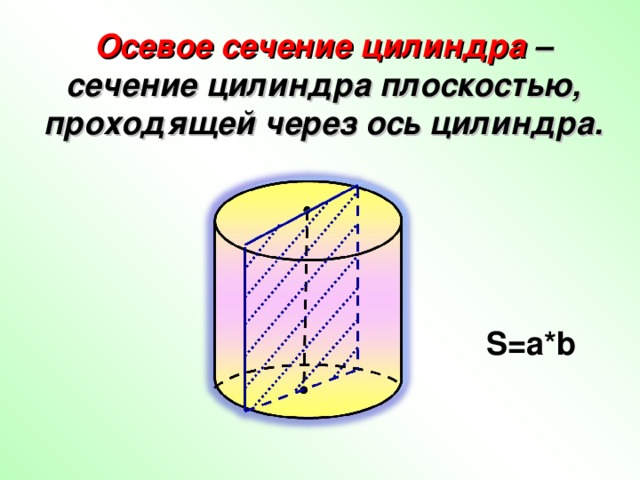
Осевое сечение цилиндра – сечение цилиндра плоскостью, проходящей через ось цилиндра.

S=a*b

Сечение цилиндра плоскостью, параллельной к оси.

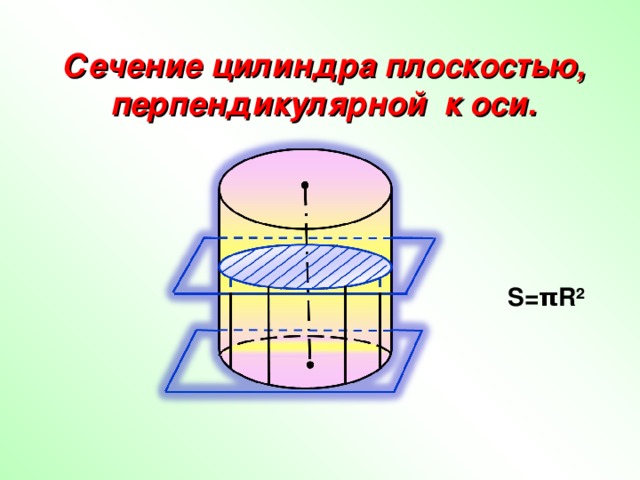
Сечение цилиндра плоскостью, перпендикулярной к оси.

S= π R²

Плоскость, проходящая через образующую прямого цилиндра и перпендикулярная осевому сечению, проведённому через эту образующую, называется касательной плоскостью цилиндра

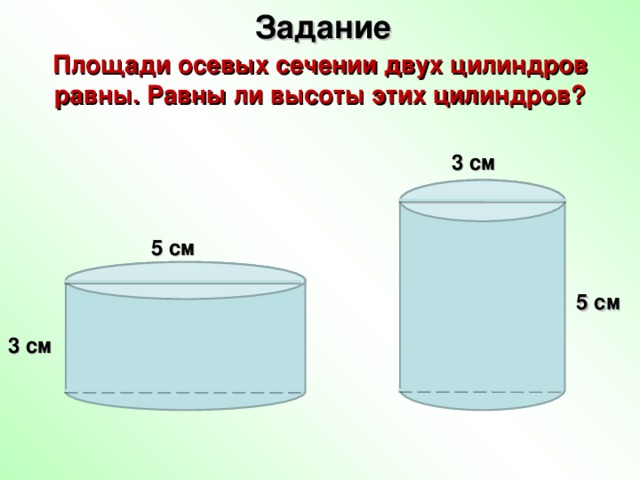
Задание

Площади осевых сечении двух цилиндров равны. Равны ли высоты этих цилиндров?

3 см

5 см

5 см

3 см

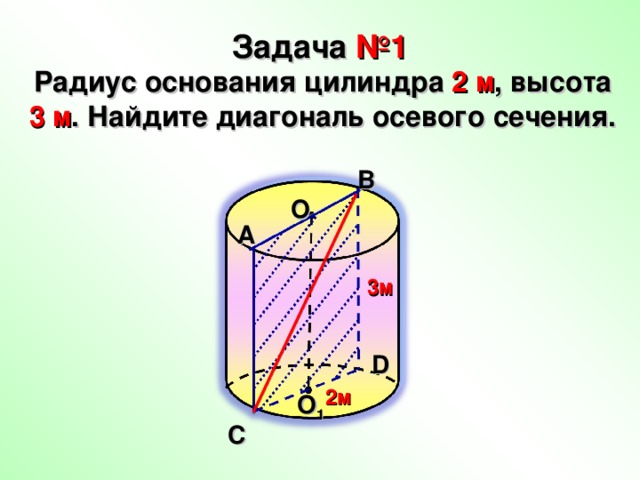
Задача №1

Радиус основания цилиндра 2 м , высота 3 м . Найдите диагональ осевого сечения.

В

О

А

3м

D

2м

О 1

С

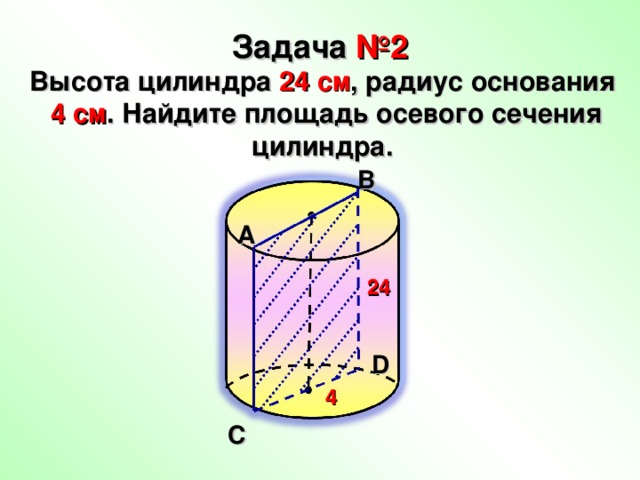
Задача №2

Высота цилиндра 24 см , радиус основания 4 см . Найдите площадь осевого сечения цилиндра.

В

А

24

D

4

С

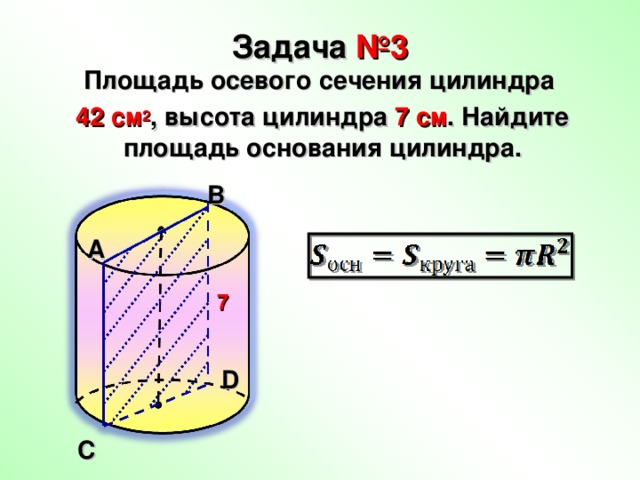
Задача №3

Площадь осевого сечения цилиндра

42 см 2 , высота цилиндра 7 см . Найдите площадь основания цилиндра.

В

А

7

D

С

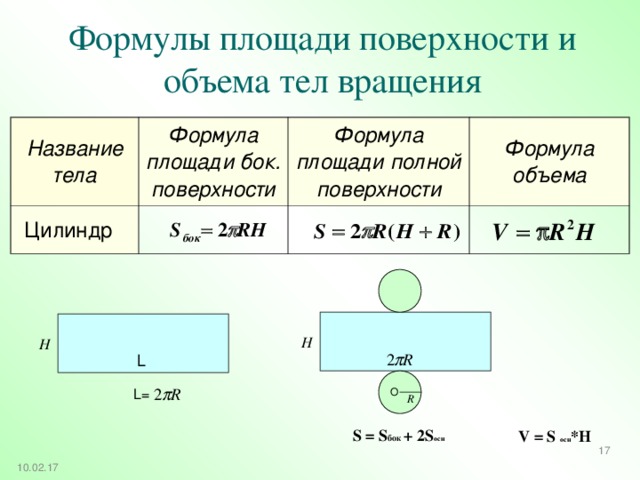
Формулы площади поверхности и объема тел вращения

Название тела

Формула площади бок. поверхности

Цилиндр   

Формула площади полной поверхности

Формула объема

L

L=

O

S = S бок + 2 S осн

V = S осн *H

10.02.17

1,5, значит смесь переливаться не будет . " width="640"

Задача №4, стр. 24.Сборник задач по математике с профессиональной направленностью (методическое пособие)

Цилиндрическая форма имеет диаметр 20 см и высоту 6 см. В неё выливают 1 л смеси для пудинга, объём которой при кипячении увеличивается в 1,5 раза. Не будет ли пудинг переливаться через край формы?

Решение.

V = πR 2 H ;

D=20 cm, R=10cm

V = 3,14·100·6 = 1881 см 3 = 1,881л - объём формы;

1 литр = 1000 cm ²

1000·1,5 = 1500см²=1,5 л – объём смеси.

1,881 1,5, значит смесь переливаться не будет .

Пудинг творожный с орехами

Ингредиенты: творог - 500г; яйцо - 5 шт.; сахар - 1/2 стакана; сухари – 4 ст.л.; изюм - 10г; орехи - 50г; цедра лимона; сливочное масло - 3 ст.л.

Способ приготовления.

Толченые сухари просеять сквозь решето. Орехи мелко нарубить, поджарить в духовке до светло-коричневого цвета и растереть с 2 ст. л. сахара. Изюм очистить и промыть в теплой воде. B протертый сквозь сито творог прибавить сахар, 3 ст. л. растопленного масла, яичные желтки, 1/2 чайной л. соли, лимонную цедру и тщательно взбить. 3атем смешать творожную массу с сухарями, орехами, изюмом, добавить взбитые в густую пену яичные белки и перемешать все.

Форму для пудинга смазать внутри маслом, посыпать песком и наполнить творожной массой. Форму заполнить на 3/4, закрыть крышкой и поместить в большую кастрюлю с водой (вода должна заполнять 1/2 высоты формы). На дно кастрюли положить толстую бумагу или марлю.

Кастрюлю накрыть крышкой и варить пудинг примерно 1 час, подливая воду. Равномерная упругость поднявшейся и слегка отставшей от краев массы является признаком готовности пудинга.

Практическая часть урока. Работа с моделями.

Каждый студент работает с моделью цилиндра, которые сами сделали.

Задание.

Вычислить по модели, используя измерительные приборы:

• Площадь полной поверхности;
• Площадь боковой поверхности;
• Площадь основания;
• Радиус;
• Высоту.

Подведение итога урока .

Вопросы:

• Встречаются ли в производственной практике предметы похожие на тела вращения? Что это за предметы?
• Какие кондитерские изделия напоминают модели круглых тел?
• Что нового и полезного для себя вы взяли с данного урока?
• Какие математические понятия использовались на уроке?
• Нужны ли вам знания по математике в профессиональной практике?
• Что нового вы узнали на уроке?
• Какие задания для вас были трудными?
• Что понравилось и не понравилось на уроке?
• Какие вопросы по новой теме возникли?

Домашнее задание:

Геометрия 6-10 кл. А. В. Погорелов.

№ 4, №8 стр. 260.

Спасибо за внимание!

10.02.17