УДК 371.335 : 51
Применение метода эвристических вопросов при изучении дисциплины «Математика»
Елена Александровна Брагина
высшая квалификационная категория
преподаватель
ГПОУ "Горловский автотранспортный техникум"
ГОУВПО "Донецкий национальный технический университет"
г. Горловка
Аннотация
Данная статья рассматривает сущность и важность эвристических вопросов при изучении математики и формировании у студентов интуитивного мышления.
Ключевые слова
Эвристические вопросы; эвристика; интуитивное мышление; творческие задачи.
Современный уровень развития образовательной системы ставит вопрос, как обеспечить высококачественное обучение и усвоение знаний в объеме стандарта образования и при этом дать возможность для дальнейшего развития. Путей решения данной проблемы, думаю, много. Модернизация образования на современном этапе рождает много педагогических открытий, больших и малых, важных и интересных для каждого преподавателя. Необходимо помнить, что образование в наше время должно быть направлено на развитие личности и способностей обучающихся, на их подготовку к взрослой жизни. Необходимо стремиться к выполнению главной заповеди учителя: «Учитель! Научи ученика!».
Обучая студентов математике, мы заставляем их мозг развиваться, анализировать и моделировать различные ситуации, знакомим с методами индукции и дедукции, учим познавать мир через призму логических рассуждений. На каждом этапе изучения математики от получения необходимых знаний, умений и навыков до развития творческих способностей и интуитивного мышления можно применять эвристические вопросы для решения различных по сложности творческих задач.
«Эврика!» – это восклицание древнего ученого и изобретателя Архимеда знакомо всем со школьной скамьи. Это слово не просто констатация факта находки, в нашем сознании оно ассоциируется с выражением высшего чувства удовлетворения, радости и восторга от найденного решения задачи, которую до этого никому не удавалось решить. 2000 лет прошло, как в лексиконе появилось слово «эвристика». Сейчас оно нашло широкое распространение. «Эвристическое мышление», «эвристические приемы и методы», «эвристическое вопросы» и т.д. – произнося эти слова, мы не всегда задумываемся над тем, какой смысл вкладываем в понятие «эвристика», но в нашем сознании оно всегда связано с творческой деятельностью [1].
Эвристические или ключевые вопросы служат дополнительным стимулом, формируют новую стратегию и тактику решения творческой задачи. В педагогике эти вопросы называют наводящими, так как правильная их постановка наводит обучающегося на правильный ответ на вопрос или решение практического задания.
С древнейших времен многие математики занимались поиском общих эвристик – общих эвристических схем, которые помогают в поиске способа решения конкретных задач. Разработкой таких эвристических схем занимался Папп (один из комментаторов Эвклида), великие математики Рене Декарт, Готфрид Лейбниц. Бернард Больцано составил интересное и подробное изложение эвристик. Кроме того, русские математики Л.М. Фридман и М.Б. Балк разработали эвристические системы для поиска решения математической задачи и успешно их использовали в своей практической работе с обучающимися [2].
Древнеримский теоретик ораторского искусства Квинтилиан рекомендовал своим ученикам ставить перед собой семь вопросов: кто? (субъект), что? (объект), зачем? (цель), где? (место), чем? (средства), как? (метод), когда? (время). Соединение этих вопросов в определенной последовательности может дать массу новых и неожиданных вопросов, способствует развитию творческих способностей и интуитивного мышления.
Эвристическим вопросам уделял много внимания американский математик и педагог Д. Пойя, исследования которого стали основой правил систематизации эвристических вопросов.
На основе рекомендаций Д. Пойя, B. И.Андреев составил следующие эвристические вопросы, стимулирующие решение творческих задач.
1. Нужно ясно понять предложенную задачу, а для этого необходимо поставить перед собой ряд вопросов и заданий: что неизвестно? что дано? в чем состоит условие? возможно ли удовлетворить условию? достаточно ли условие для определения неизвестного? или недостаточно? или чрезмерно? или противоречиво? сделайте чертеж; введите подходящее обозначение; разделите условие на части; постарайтесь записать их.
2. На этапе поиска идей и составления плана решения ставятся следующие эвристические вопросы: как найти связь между данными и неизвестными? не известна ли вам какая-нибудь родственная задача? нельзя ли ею воспользоваться? нельзя ли использовать метод ее решения? не следует ли ввести какой-либо вспомогательный элемент, чтобы воспользоваться прежней задачей? нельзя ли сформулировать задачу иначе, проще? нельзя ли придумать более доступную задачу? более общую? более частную? аналогичную задачу? нельзя ли решить часть задачи, удовлетворить часть условий? нельзя ли извлечь что-либо полезное из данных? все ли данные и условия вами использованы? приняты ли во внимание все понятия, содержащиеся в задаче?
3. Осуществляя план решения, контролируйте каждый свой шаг: ясно ли вам, что предпринятый вами шаг правилен? сумеете ли доказать, что он правилен?
4. Контроль и самоконтроль полученного решения предполагает поиск ответов на такие вопросы, как: нельзя ли проверить результат? нельзя ли проверить ход решения? нельзя ли получить тот же результат иначе? нельзя ли проверить правдоподобность, размерность полученного результата? нельзя ли в какой-нибудь другой задаче использовать полученный результат? нельзя ли решить задачу, обратную этой?
Применяя эвристические вопросы для решения творческих задач, преподаватель вместо сообщения готовых знаний и алгоритмов решения заставляет обучающихся прийти к новым понятиям, выводам, моделям решения. Осуществляется это путем правильно поставленных вопросов со стороны преподавателя и задействования обучающимися своего опыта, имеющихся знаний и наблюдений. Для демонстрации применения эвристических вопросов нет необходимости рассматривать сложные задачи. Значимость эвристических вопросов можно продемонстрировать при решении несложных творческих задач.
Рассмотрим некоторые творческие задачи и пути их решения при помощи физического и геометрического смысла производной с использованием эвристических вопросов. Прямые задачи по данной теме можно решить без наводящих вопросов с использованием формул.
Задача 1.
Найти момент времени t, когда тело, которое движется по закону S(t), будет иметь скорость (ускорение) V м/с (а м/с2).
Итак, какие эвристические вопросы и в каком порядке нужно поставить перед обучающимися для решения данной задачи? Перечислим эти вопросы:
1) Что дано?
Ответ: закон движения S(t) и скорость (ускорение) V м/с (а м/с2).
2) Что неизвестно?
Ответ: момент времени t.
3) Как найти связь между данными и неизвестными и решить задачу?
Ответ: зная закон движения S(t), мы можем найти закон скорости V (t) (закон ускорения а(t)) и, зная конкретное значение скорости (ускорения), решить уравнение V (t) = V ( а (t) = а).
Сформулируем условие другой задачи.
Задача 2. Найти момент времени t, когда тело, которое движется по закону S(t), остановится.
Рассмотрим эвристические вопросы, которые помогут определить путь решения данной задачи:
1) Что дано?
Ответ: закон движения S(t).
2) Что неизвестно?
Ответ: момент времени t.
3) Все ли данные и условия вами использованы?
Ответ: в условии говорится об остановке тела.
4) что для движения означает остановка тела?
Ответ: если тело останавливается, то V = 0 м/с.
5) Как найти связь между данными и неизвестными и решить задачу?
Ответ: для решения этой задачи необходимо найти V (t) и решить уравнение V (t) = 0.
Задача 3. Составить уравнение касательной к кривой, если уравнение нормали к этой кривой в той же точке имеет вид 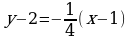 .
.
Для решения поставим эвристичекие вопросы:
1) что дано?
Ответ: имеем уравнение нормали 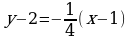 .
.
2) что неизвестно?
Ответ: уравнение касательной.
3) что необходимо для составления уравнения касательной?
Ответ: 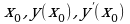 .
.
4) нельзя ли извлечь что-либо полезное из уравнения нормали?
Ответ: сопоставляя общее и данное уравнение нормали получаем: 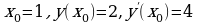 .
.
5) достаточно ли эти данных для составления уравнения касательной?
Ответ: да.
6) как составить уравнение касательной?
Ответ: возьмем формулу уравнения касательной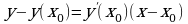 , полученные данные
, полученные данные 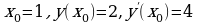 и составим необходимое уравнение: 4x-y-2=0.
и составим необходимое уравнение: 4x-y-2=0.
Даже в несложных творческих задачах видно, что эвристические вопросы задают наиболее вероятностные стратегии и тактики деятельности решающего, стимулируют его интуитивное мышление в процессе решения, генерируют новые идеи и на этой основе существенно повышают эффективность решения творческих задач. Кроме того, использование эвристических вопросов сокращает время решения задачи по сравнению с формальными методами и алгоритмами [1].
Список использованных источников
1. Большая Советская Энциклопедия, 1978. Том 29.
2. Пойа Д. Как решать задачу. – Львов: журнал “Квантор”,1991.
3. Пушкин В.Н. Эвристика – наука о творческом мышлении. – М.: Политиздат, 1967.







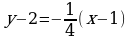 .
.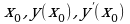 .
.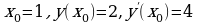 .
.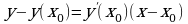 , полученные данные
, полученные данные 









