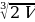ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ ПРОИЗВОДНОЙ ДЛЯ НАХОЖДЕНИЯ НАИЛУЧШЕГО РЕШЕНИЯ В ПРИКЛАДНЫХ ЗАДАЧАХ.
(Раздел «Начала математического анализа»)
ДЕЯТЕЛЬНОСТНАЯ КАРТА УЧЕБНОГО ЗАНЯТИЯ
Профессии: 15.01.20 Слесарь по контрольно-измерительным приборам и автоматике, 09.01.03 Мастер по обработке цифровой информации, 23.01.03 Автомеханик, 09.01.01 Наладчик аппаратного и программного обеспечения
Учебные группы: КИП-11, М-11, А-11, Н-11
Учебная дисциплина: ООПу.04 Математика
Тема учебного занятия: Примеры использования производной для нахождения наилучшего решения в прикладных задачах.
Тип урока: урок «открытия» новых знаний
Вид урока: лекция-беседа
Средства обучения:
технические: мультимедийный проектор, персональный компьютер;
информационно-коммуникационные: электронная презентация.
Цели урока:
методическая: использование объяснительно-иллюстративного метода обучения с целью формирования математического мышления студентов;
образовательная: создание условий для овладения знаниями о примерах использования производной для нахождения наилучшего решения в прикладных задачах;
развивающая: развитие умений планировать, анализировать, выдвигать гипотезы по решению заданий, применять полученные знания для выполнения упражнений;
воспитательная: воспитание интереса к изучению математики, математической культуры студентов.
Прогнозируемые результаты:
1) предметные:
сформированность знаний о вычислениях пределов последовательностей;
владение умением решать задачи на пределы последовательностей;
2) метапредметные:
умение ставить перед собой цель, видеть ожидаемый результат работы;
умение рационально распределять рабочее время;
умение объективно оценивать свои возможности, анализировать свои результаты, корректировать свои действия;
владение навыками познавательной рефлексии;
умение осуществлять поиск и отбор необходимой информации;
умение сопоставлять и анализировать, выделять в тексте базовые и вспомогательные концепты, опорные понятия, тезисы, структурировать их взаимосвязь;
умение структурировать полученную информацию;
умение анализировать и обобщать информацию;
умение продуктивно общаться и взаимодействовать в процессе совместной деятельности, учитывать позиции других участников деятельности;
умение выражать свои мысли с достаточной полнотой и точностью.
Образовательные технологии: традиционное обучение.
Формы организации обучения: фронтальная, индивидуальная.
Методы обучения и контроля:
вербальные: беседа;
практические: метод сравнения, метод анализа и структурирования.
методы контроля и самоконтроля: устный контроль, самоконтроль.
Нормативный документ
Федеральный государственный образовательный стандарт среднего общего образования (утв. приказом Министерства образования и науки Российской Федерации (Минобрнауки России) от 17 мая 2012 г. № 413 г.). – М.: Министерство образования и науки РФ, – 2012.
Образовательные ресурсы:
Основная литература
Башмаков М. И. Математика: учебник для студ. учреждений сред. проф. образования. − М.: Издательский центр «Академия», 2018. – 256 с.
Башмаков М. И. Математика. Сборник задач профильной направленности: учеб. пособие для студ. учреждений сред. проф. образования. − М.: Издательский центр «Академия», 2014. – 416 с.
Дополнительная литература
Алимов Ш.А., Колягин Ю.М. Алгебра и начала математического анализа (базовый и углубленный уровни).10—11 классы. Учебник. − М.: Просвещение, 2014. – 464 с.
Атанасян Л.С. Геометрия. 10 − 11 классы: учебник для общеобразовательных учреждений: базовый и профильный уровни / Атанасян Л.С., Бутузов В.Ф. и др. – М.: Просвещение, 2013. – 255 с.
Богомолов Н.В. Практические занятия по математике: Учеб. пособие для техникумов / Н.В. Богомолов. – М.: Высш. шк., 2013. – 495 с.
Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика (Книга 1): Учебное пособие. – М.: Издательство «Новая волна», 2013. – 656 с.
Колягин Ю.М., Луканкин Г.Л., Яковлев Г.Н. Математика (Книга 2): Учебное пособие. – М.: Издательство «Новая волна», 2013. – 592 с.
Никольский С.М. Алгебра и начала анализа: учебник для 10 класса общеобразоват. учреждений: базовый и профильный уровни / С.М. Никольский, М.К. Потапов. – М.: Просвещение, 2013. – 430 с.
Никольский С.М. Алгебра и начала анализа: учебник для 11 класса общеобразоват. учреждений: базовый и профильный уровни / С.М. Никольский, М.К. Потапов. – М.: Просвещение, 2013. – 464 с.
Интернет-ресурсы:
Федеральный центр информационно-образовательных ресурсов [Электронный ресурс] URL: www. fcior. edu. ru
Единая коллекции цифровых образовательных ресурсов [Электронный ресурс] URL: www. school-collection. edu. ru
Научно-методические ресурсы:
Инновационные педагогические технологии: учебное пособие/ Михелькевич В.Н., Нестеренко В.М., Кравцова П.Г. – Самар. гос. тех. ун-т Самара, 2001. – 89 с.
Кульневич С.В., Лакоценина Т.П. Современный урок. Часть 1: Научно-практич. пособие для учителей, методистов, руководителей учебных заведений, студентов пед. заведений, слушателей ИПК. – Ростов н/Д: Учитель, 2005. – 288 с.
Кульневич С.В., Лакоценина Т.П. Современный урок. Часть 3: Научно-практич. пособие для учителей, методистов, руководителей учебных заведений, студентов пед. заведений, слушателей ИПК. – Ростов н/Д: Учитель, 2007. – 288 с.
Махмутов М.И. Проблемное обучение: Основные вопросы теории. – М.: Педагогика, 1975. – 368 с.
Основные термины и понятия: примеры использования производной, прикладные задачи.
ПЛАН УЧЕБНОГО ЗАНЯТИЯ
Содержание учебного материала:
1) Сформированность знаний о примерах использования производной для нахождения наилучшего решения в прикладных задачах.
2) Закрепление теоретического материала по теме с помощью решения упражнений.
Этап мотивации (самоопределения) к учебной деятельности (2 мин)
Преподаватель приветствует студентов, создает деловую обстановку, настраивает на продуктивную мыслительную деятельность.
Этап актуализации опорных знаний. Целеполагание (15 мин)
Преподаватель задает вопросы студентам:
Какие вы знаете методы исследования функции?
Как находить наибольшее и наименьшее значений непрерывной функции на промежутке?
Как применять производную на нахождение наибольшего и наименьшего значений непрерывной функции на промежутке.
Студенты отвечают на эти вопросы, вспоминая знания, полученные на предыдущем занятии.
Формулирование темы и целей учебного занятия.
Работа над новой темой («открытие» нового знания) (48 мин)
Алгоритм работы над «открытием» нового знания:
Формулирование преподавателем определений о примерах использования производной для нахождения наилучшего решения в прикладных задачах.
Найти наибольшее, наименьшее значения функции 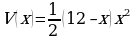 на отрезке
на отрезке 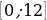 . Это и проверка усвоения темы прошлого урока, и возможность просмотреть домашнее задание (собрать коробочки), и главное, переходное задание к задачам на оптимизацию. Работу обязательно проверяю по решению одного из учащихся на обратной стороне доски.
. Это и проверка усвоения темы прошлого урока, и возможность просмотреть домашнее задание (собрать коробочки), и главное, переходное задание к задачам на оптимизацию. Работу обязательно проверяю по решению одного из учащихся на обратной стороне доски.
К объяснению темы приступаю с демонстрации исходного квадрата и тех коробочек, которые изготовили учащиеся, с указанием их объёмов. Бумажный квадрат был у всех одинакового размера, а объёмы коробочек получились разные. Выясняем, в каком случае коробочка имеет наибольший объём. Пусть 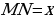 см (см. рисунок).
см (см. рисунок).
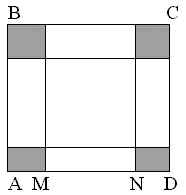
Тогда 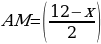 см, объём коробочки:
см, объём коробочки: 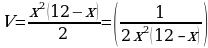 см, где
см, где 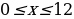 . Находим наибольшее значение функции
. Находим наибольшее значение функции 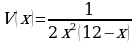 на отрезке
на отрезке 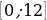 . Эта задача была решена в начале урока. Таким образом, в этой части урока всё внимание сосредотачивается на составление математической модели задачи. Важно выяснить, так чья же коробочка имеет наибольший объём?
. Эта задача была решена в начале урока. Таким образом, в этой части урока всё внимание сосредотачивается на составление математической модели задачи. Важно выяснить, так чья же коробочка имеет наибольший объём?
П.Л.Чебышев говорил, что «особенную важность имеют те методы науки, которые позволяют решать задачу, общую для всей практической деятельности человека: как располагать своими средствами для достижения наибольшей выгоды». С такими задачами в наше время приходится иметь дело представителям самых разных специальностей. Технологи – стараются так организовать производство, чтобы выпускалось как можно больше продукции. Конструкторы пытаются разработать прибор для космического корабля так, чтобы масса прибора была наименьшей. Экономисты стараются спланировать связи завода с источниками сырья так, чтобы транспортные расходы оказались минимальными, и т.д.
Задачи подобного рода носят общее название – задачи на оптимизацию (от латинского слова optimum – «наилучший»). В самых простых задачах на оптимизацию мы имеем дело с двумя величинами, одна из которых зависит от другой, причём надо найти такое значение второй величины, при котором первая принимает своё наименьшее или наибольшее (наилучшее в данных условиях) значение.
Включение нового знания в систему имеющихся знаний (20 мин)
Периметр прямоугольника равен 40 см. Какую длину должны иметь стороны прямоугольника, чтобы площадь была наибольшей?
Решение: 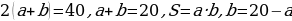 .
.
Выбираем независимую переменную х и выражаем через неё стороны прямоугольника. х см – длина прямоугольника, 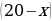 см – ширина прямоугольника. Тогда
см – ширина прямоугольника. Тогда 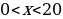 ;
;
записываем функцию 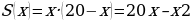 ;
;
находим производную 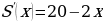 ;
;
решаем уравнение 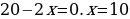 .
.
Значит, длина и ширина равны 10 см. Какая это получается фигура? (Квадрат).
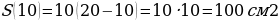 .
.
Ответ: 10 см.
Бак, имеющий вид прямоугольного параллелепипеда с квадратным основанием, должен вмещать 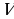 литров жидкости. При какой стороне основания площадь поверхности бака (без крышки) будет наименьшей?
литров жидкости. При какой стороне основания площадь поверхности бака (без крышки) будет наименьшей?
Решение. Первый этап. Составление математической модели.
1) Оптимизируемая величина — площадь поверхности бака, поскольку в задаче требуется выяснить, когда эта площадь будет наименьшей. Обозначим 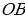 буквой
буквой 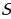
2) Площадь поверхности зависит от измерений прямоугольного параллелепипеда. Объявим независимой переменной (Н. П.) сторону квадрата, служащего основанием бака; обозначим ее буквой 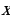 Ясно, что
Ясно, что 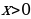 Других ограничений нет, значит,
Других ограничений нет, значит,
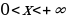 Таковы реальные границы изменения независимой переменной:
Таковы реальные границы изменения независимой переменной:
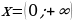
3) Если 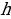 — высота бака, то
— высота бака, то 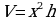 , откуда находим
, откуда находим 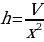
На рис. изображен прямоугольный параллелепипед, указаны его измерения. Поверхность бака состоит из квадрата со стороной 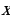 и четырех прямоугольников со сторонами
и четырех прямоугольников со сторонами 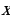 и
и 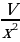 . Значит,
. Значит, 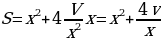
Итак, 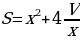 , где
, где 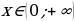
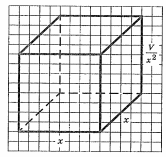
Математическая модель задачи составлена.
Работа с составленной моделью.
На этом этапе для функции 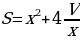 , где
, где 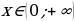 надо найти
надо найти 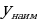 . Для этого нужна производная функции:
. Для этого нужна производная функции:
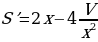
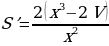
На промежутке 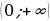 критических точек нет, а стационарная точка только одна:
критических точек нет, а стационарная точка только одна: 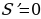 при
при 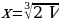
Заметим, что при 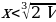 выполняется неравенство
выполняется неравенство 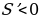 , а при
, а при 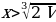 выполняется неравенство
выполняется неравенство 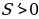 . Значит,
. Значит, 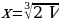 — единственная стационарная точка, причем точка минимума функции на заданном промежутке, а потому, согласно теореме, в этой точке функция достигает своего наименьшего значения.
— единственная стационарная точка, причем точка минимума функции на заданном промежутке, а потому, согласно теореме, в этой точке функция достигает своего наименьшего значения.
В задаче спрашивается, какой должна быть сторона основания, чтобы бак имел наименьшую поверхность. Мы выяснили, что сторона квадрата, служащего основанием такого бака, равна 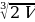
Рефлексия. Подведение итогов учебного занятия (5 мин)
Беседа со студентами по содержанию занятия. Вопросы для беседы:
Какая была тема сегодняшнего занятия?
Что нового вы узнали?
Какая была цель занятия?
Что получилось у вас сегодня?
Что не получилось?
Достигли ли мы поставленной цели?
Инструктирование о выполнении домашнего задания
Изучить [1] гл. 9 занятие 7







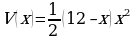 на отрезке
на отрезке 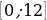 . Это и проверка усвоения темы прошлого урока, и возможность просмотреть домашнее задание (собрать коробочки), и главное, переходное задание к задачам на оптимизацию. Работу обязательно проверяю по решению одного из учащихся на обратной стороне доски.
. Это и проверка усвоения темы прошлого урока, и возможность просмотреть домашнее задание (собрать коробочки), и главное, переходное задание к задачам на оптимизацию. Работу обязательно проверяю по решению одного из учащихся на обратной стороне доски.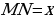 см (см. рисунок).
см (см. рисунок).
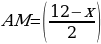 см, объём коробочки:
см, объём коробочки: 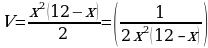 см, где
см, где 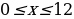 . Находим наибольшее значение функции
. Находим наибольшее значение функции 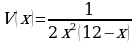 на отрезке
на отрезке 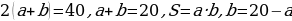 .
.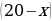 см – ширина прямоугольника. Тогда
см – ширина прямоугольника. Тогда 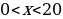 ;
;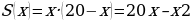 ;
;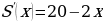 ;
;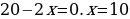 .
.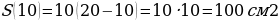 .
.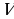 литров жидкости. При какой стороне основания площадь поверхности бака (без крышки) будет наименьшей?
литров жидкости. При какой стороне основания площадь поверхности бака (без крышки) будет наименьшей?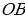 буквой
буквой 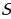
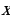 Ясно, что
Ясно, что 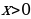 Других ограничений нет, значит,
Других ограничений нет, значит, 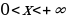 Таковы реальные границы изменения независимой переменной:
Таковы реальные границы изменения независимой переменной: 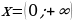
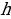 — высота бака, то
— высота бака, то 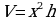 , откуда находим
, откуда находим 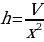
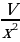 . Значит,
. Значит, 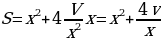
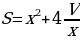 , где
, где 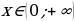

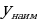 . Для этого нужна производная функции:
. Для этого нужна производная функции: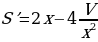
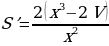
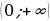 критических точек нет, а стационарная точка только одна:
критических точек нет, а стационарная точка только одна: 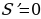 при
при 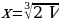
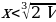 выполняется неравенство
выполняется неравенство 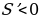 , а при
, а при 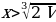 выполняется неравенство
выполняется неравенство  . Значит,
. Значит,