"Применение подобия треугольников"

Применение подобия треугольников

Выполнил

Гречкин Владислав,

ученик 8 класса

МБОУ ООШ р. п.Чаадаевка имени Героя Советского Союза Н. Ф. Горюнова

Цель: Изучение применения подобия треугольников в решении задач и при измерительных работах на местности.

Задачи:

• Уметь применять признаки подобия треугольников при решении геометрических задач на местности.
• Разобрать решения задач различного уровня сложности, решаемые методом подобия.
• Провести практическую работу.

Геометрия полна приключений, потому

что за каждой задачей скрывается

приключение мысли.

Решить задачу – это значит

пережить приключение.

В. Произволов

Фалес Милетский

(625 до н. э. – 548 до н. э.)

Подобие вокруг нас

Определение

Признаки подобия треугольников

Площадь треугольника АВС равна 12, ЕD – средняя линия треугольника АВС. Найдите площадь трапеции АЕDВ.

.

Решение.

ЕD – средняя линия ∆ АВС, значит ЕD||АВ.

В ∆ ЕСD и ∆ АСВ: ∠ С – общий, ∠ СЕD = ∠ A (соответственные при АВ||DЕ и секущей АС), значит ∆ АВС ~ ∆ ЕDС (по двум углам),

значит

Ответ: 8.

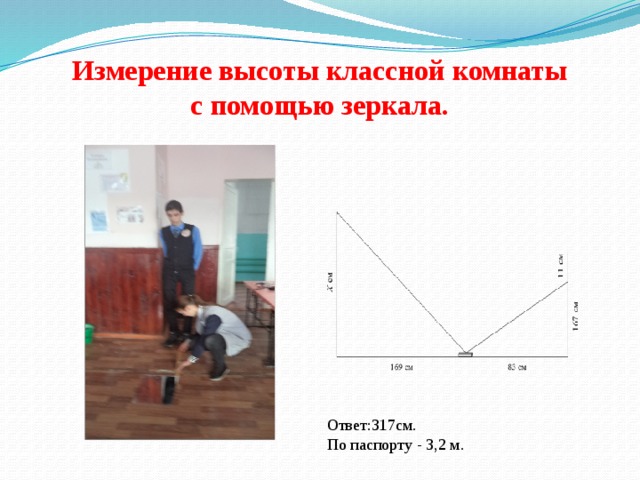
Измерение высоты классной комнаты с помощью зеркала.

Ответ:317см.

По паспорту - 3,2 м.

Измерение высоты сосны с помощью палки с вращающейся планкой.

Получил 6,3 м.

Измерение высоты предмета с помощью эклиметра и высотомера.

9,9+1,67=11,57 м

10 м.

Измерение высоты школы с помощью равнобедренного прямоугольного треугольника.

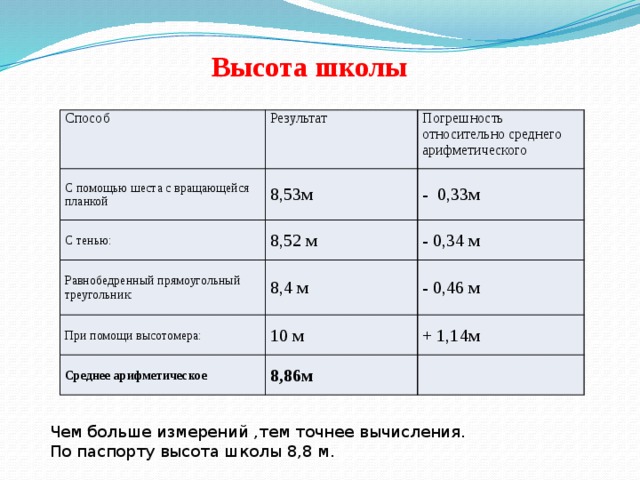
Высота школы

Способ

Результат

С помощью шеста с вращающейся планкой

Погрешность относительно среднего арифметического

8,53м

С тенью:

8,52 м

- 0,33м

Равнобедренный прямоугольный треугольник:

При помощи высотомера:

8,4 м

- 0,34 м

10 м

- 0,46 м

Среднее арифметическое

+ 1,14м

8,86м

Чем больше измерений ,тем точнее вычисления.

По паспорту высота школы 8,8 м.

Измерение расстояния до недоступной точки с помощью астролябии.

Получилось 561 м.

Выводы:

• Применение подобия треугольников незаменимы в нахождении высоты объекта.
• Результаты исследования получаются более точные, если мы более точно измеряем расстояние до объекта.
• Существует большое количество способов измерения высоты объекта и расстояния до недоступной точки.
• Приборы для измерения могут быть сделаны своими руками.