Проект Функции вокруг нас

Департамент образования, науки и молодежной политики Воронежской области

Государственное бюджетное профессиональное
образовательное учреждение Воронежской области
«Лискинский промышленно-транспортный техникум имени А.К. Лысенко»

(ГБПОУ ВО «ЛПТТ имени А.К. Лысенко»)

Индивидуальный проект.

Тема:Функции вокруг нас.

Выполнил студент группы 919 ИС

Завилохин Даниил

Руководитель: преподаватель

математики Михеева С.В.

Введение

Актуальность
Образование, в наше время, является незаменимой частью жизни любого человека. Для людей, изучающих технические науки особенно важна математика. Функции являются одним из фундаментальных инструментов для дальнейшего изучения математики. Кроме того, функции окружают нас. Любое действие, которое имеет две и больше вариаций, будет иметь свою функцию.

Цель работы:

• Выявить нестандартное применение математических функций в окружающем нас мире

Задачи:

1. Узнать что такое "функция"

2. Узнать историю возникновения функций

3. Выяснить применение функций в математике

4. Найти примеры из окружающего мира, в которых требуется применение функций

I. Функции в математике

1. Из истории возникновения функции. Определения функции.

Первый раз, люди осознали, что все явления, которые окружают их связаны друг с другом, очень давно. Тогда они ещё не обладали навыками чтения и счёта, но уже на практике могли определять несложные закономерности и делали заключения. С развитием науки и технологий количество и сложность всех взаимосвязей росло.

Идея функции исходит из очень давних времен, её используют уже в самых первых математических выражениях, в первых правилах взаимодействия с числами, а так же в первых формулах нахождения площади геометрических фигур.

В первой половину XVII в. из-за активного развития механики, в математике появляются идеи движения и изменения. В то же самое время складывается представление о функции как о зависимости одной переменной от величины другой.

Ещё не было сформулировано четкого определения функции. Однако первопроходцем в этой теории стали Рене Декарт и Пьер Ферма, которые представляли функцию как зависимость ординаты точки кривой от ее абциссы.

В первый раз, задокументированный случай использования термина “функция” было использовано Лейбницем в 1692 году. Он был связан с геометрическим образом – графиком.

А общее определение функции было дано только в 1834 году нашим соотечественником Николаем Лобачевским.

Термин “функция” можно считать по-сути базой, вокруг которой строится изучение математике. Только функция может в полной мере отразить настоящие, реальные явления с такой конкретностью.

У функции существуют несколько определений. При этом каждое из них дополняет другое:

1. Функция – это взаимосвязь между величинами или же зависимость одной переменной от другой. Любая формула или закон физики отражает значение данного определения.

Формула знакомая всем школьникам объясняет идею зависимости одной величины от другой. Переменная у зависит от переменной x по правилу, обозначенному как f.

2. Функция – это определенное действие над переменной.

Это значит, что мы воспроизводим какие-либо действия с переменной x, и получаем переменную y.

3. В технической литературе встречается определение функции как устройства, на вход которого подается x, а на выходе получается .

Итак, в данном случае, функция – это действие над переменной.

4. Определение функции, чаще всего встречающееся в учебниках.

Функция – это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один и только один элемент второго множества.

2. Способы задания функции. Виды функций, типы функций, некоторые характеристики.

Функция является известной, если можно узнать соответствующее значение функции у каждого возможного числа аргументов. Наиболее распространенные три способа задания функции: табличный, графический, аналитический.

1. Табличный способ самый распространенный способ (таблицы  квадратных и кубических корней), главным достоинством является – возможность получения числового значения функции, недостатки заключаются в том, что таблица может быть слишком громоздка, а из-за этого трудночитаема. (Приложение I)

 2. Графический способ заключается в проведении графика у которой абсциссы изображают значения аргумента, а ординаты – соответствующие значения функции. Часто для наглядности масштабы на осях принимают разными. (Приложение II)

Достоинства этого способа задания функций заключаются в легкости и целостности восприятия, в непрерывности изменения аргумента; недостатком является уменьшение степени точности и сложность получения точных значений.

 3. Аналитический способ состоит в задании функции одной или несколькими формулами. Основным достоинством этого способа является высокая точность определения функции от интересующего аргумента, а недостатком является затрата времени на проведение дополнительных математических операций.

II Функции вокруг нас

2.1. Мой первый в жизни график.

Каждый год родители отмечали мой рост. Это наглядный пример табличной функции.

Когда я вырос, я построил график моего роста, он отражает зависимость моего роста от времени. (Приложение III).

2.2. Кардиограмма – график работы сердца

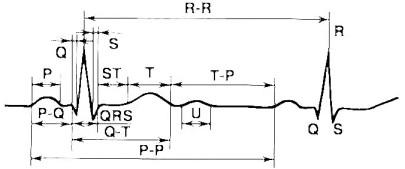Кардиограмма – график работы сердца. Это один из самых явных примеров графической функции. На графике можно увидеть максимум и минимум, фрагменты линейной функции, сглаживание линий и т.д.

Кардиограмма – это запись сокращений сердца человека, которая осуществляется при помощи какого-либо инструментального способа. Во время сокращения сердце передвигается в пределах грудной клетки, оно вращается вокруг своей оси слева направо.

Суть электрографии заключается в том, чтобы зарегистрировать разности потенциала во времени. Кривая, которая показывает нам эти изменения и есть кардиограмма. Прибор, который записывает эту кривую, именуется электрокардиографом. Кардиограмма сердца показывает возбуждение сердца и его сокращение. Во время снятия кардиограммы к телу человека прикрепляются специальные электроды, благодаря которым аппарат и получает необходимые данные.

Суть обработки сигналов данного исследования заключается в том, чтобы диагностировать имеющиеся проблемы в работе сердечных мышц, используя при этом различные аналитические методы. Чтобы диагноз был правильным, прежде всего, необходимо точно установить все особые участки электрокардиограммы в лице зубцов. Здесь в первую очередь важны точная точка их начала и конца. Благодаря этим данным можно вычислить точную ширину, а также амплитуду этих самых зубцов. Именно эти данные чрезвычайно важны для функционального анализа данного исследования. Самой главной проблемой в анализе кардиограммы является то, что все зубцы на ней имеют разную форму, ширину и амплитуду. Довольно часто на некоторых участках кардиограммы зубцов вообще нет.

Ср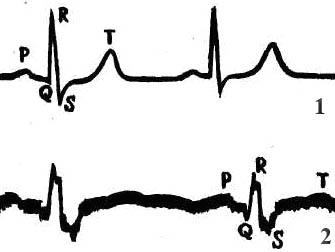 авнивая электрокардиограммы здорового (1) и больного (2) сердца, можно увидеть четкое различие между ними и судить о характере поражения сердечной мышцы. Форма и вид зубцов, длительность и вид промежутков кардиограммы напрямую связаны с фазами возбуждения и расслабления мышц сердца. Работу предсердий характеризует зубец Р (восходящий участок – возбуждение правого, нисходящий – левого предсердий), а промежуток времени, когда действуют оба предсердия, называется PQ. Зубцы Q и R показывают активность нижней и верхней частей сердца. В этот же промежуток времени активны желудочки (их наружные части). Сегмент ST – это активность обеих желудочков, а зубец Т означает переход мышц сердца в нормальное состояние….

И вот так, анализируя каждый участок кардиограммы, врач-кардиолог делает выводы и ставит диагноз. Ему приходится исследовать функцию кардиограммы по разным параметрам. Сравнивать с эталоном по всем критериям, проводить расчеты, сопоставлять цифры.

2.3. Я за чаем не скучаю

Я очень люблю чай и кофе. Люблю пить его как в одиночестве, так и всей семьей. Однажды мне стало интересно, и я решил построить график зависимости закипания воды от ее (воды) объема. (приложение IV).

Конечно, время закипания зависит не только от объёма воды, но и от начальной температуры воды, от чайника, от атмосферного давления и многих прочих зависимостей.

2.4. Функции в политике.

Недавно, 9 сентября 2018 года наша Воронежская область пережила важное для своего региона событие – выборы губернатора Воронежской области. Мне захотелось как-то графически обосновать этот процесс.

С помощью интернет-ресурсов я узнал, что на должность губернатора выдвинули свои кандидатуры 4 претендента, от партии «Единая Россия» Александр Гусев, от партии КПРФ Николай Воронин, от партии ЛДПР Олег Бурцев, от партии
«Справедливая Россия» Виталий Климов, от партии «Родина» Аркадий Минаков,
от «Партии Роста» Игорь Переверзенцев. На сайте wikipedia я нашел окончательные результаты выборов и построил график. (Приложение V).

На графике чётко виден большой отрыв нашего губернатора от своих конкурентов. Вообще графики обеспечивают наглядность того материала, который описывают.

2.5. «Великий и могучий русский язык…»

Давно замечено, что мудрость и дух народа проявляются в его пословицах и поговорках, а знание пословиц и поговорок того или иного народа способствует не только лучшему знанию языка, но и лучшему пониманию образа мыслей и характера народа.

У русского народа, как у любого другого, существует бесчисленное множество пословиц, поговорок, загадок. Они создавались и накапливались народом в течении многовековой его истории, они отражают его жизнь, условия труда, культуру и т.д. Также они отражают взаимосвязи, существующие между различными жизненными объектами, то есть являются отражениями функциональных зависимостей и доказывают, что функция - это сама жизнь! Математики похожи на французов: что бы вы ни сказали, они все переведут на собственный язык. Получится нечто противоположное. (Иоганн Вольфганг Гете). Даже пословицы можно переложить на язык функций.

Я рассмотрел некоторые пословицы и поговорки с точки зрения функциональной зависимости.

Прямая зависимость

Кт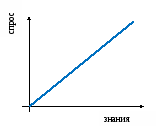 о много знает, с того много спрашивают.

Кто много живет, тот много знает.

Чем дальше в лес, тем больше дров.

Разная скорость роста функции

Без детей горе, а с детьми - вдвое

Обратная зависимость

Работает – как ребенок, а ест – как детина.

Тише едешь – дальше будешь.

М одуль

Что в лоб, что по лбу

Пр ямая

Для матери ребенок – до ста лет детенок

III. Заключение

Функция – это одно из основных общенаучных и математических понятий, выражающее зависимость между переменными величинами.

В процессе работы над темой своего исследования я начал замечать функциональную зависимость практически во всех явлениях. К сожалению, в одной работе, в очень сжатые сроки, сложно отметить все окружающие нас зависимости, но я твердо убежден, что функции находятся вокруг нас.

Список используемой литературы:

1.://educon.by/index.php/materials/math/funkcii
2.https://youclever.org/book/funktsii-1
3.http://math-prosto.ru/?page=pages/function/what_is_math_function.php
4.http://mathprofi.ru/grafiki_i_svoistva_funkcij.html
5.https://google.com/images
6.https://nsportal.ru/ap/library/nauchno-tekhnicheskoe-tvorchestvo/2014/11/14/proekt-funktsii-ryadom-s-nami
7.Н.П.Шаталова, 2010 год, “ТЕОРИЯ ФУНКЦИЙ ДЕЙСТВИТЕЛЬНОГО ПЕРЕМЕННОГО”
8.Л.Г. Петерсон, Д.Л. Абраров, Е.В Чуткова издательство: Ювента, 2011 год, “Математика. Алгебра. Функции. Анализ данных.”

Приложения

Приложение I

Приложение II

Приложение III

Приложение IV

Приложение V