Проект "Математические софизмы"

Математические софизмы

Подготовила ученица лицея №17

11«А» класса

Ершова Анастасия

Руководитель проекта: Ситникова Елена Григорьевна

Калининград

2017

Цель проекта

Изучить данную тему и сформировать умение находить ошибки в рассуждениях, давать строгие математические обоснования

Задачи

• Дать определение софизмам
• Ознакомиться с их классификацией
• Привести примеры софизмов
• Рассмотреть несколько примеров, понять ошибки и разобрать их

Определение

Софизм - формально кажущееся правильным, но по существу ложное умозаключение, основанное на неправильном подборе исходных положений.

Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно тонкие ошибки. Особенно часто в софизмах выполняют "запрещенные" действия или не учитываются условия применимости теорем, формул и правил.

Классификация софизмов

Алгебраические софизмы – это умозаключения, в которых намеренно скрытые ошибки содержатся в уравнениях, числовых или алгебраических выражениях.

Например:

65 = 64

Отрицательное число больше положительного

Все числа равны между собой

2 * 2 = 5

Геометрические софизмы – это умозаключения или рассуждения, обосновывающие какое-нибудь заведомо парадоксальное утверждение, связанное с геометрическими фигурами и действиями над ними.

Например:

Сумма длин двух сторон треугольника равна длине третьей стороны

Все треугольники - равнобедренные

Зачем нужны софизмы

• Приучают тщательно следить за точностью формулировок

• Приучают ко внимательности при построении чертежей

• Развивают наблюдательность, логику, навыки правильного мышления, критическое отношение к изучаемому

Способ нахождения ошибки в софизмах

• Лучше начать поиск ошибки с условия предложенного софизма, внимательно прочитав его. В некоторых софизмах абсурдный результат получается из-за противоречивых или неполных данных в условии, неправильного чертежа, ложного первоначального предположения, а далее все рассуждения проводятся верно. Все привыкли, что задания, предполагаемые в различной литературе, не содержат ошибок в условии и, поэтому, если получается неверный результат, то ошибку они ищут непременно по ходу решения.
• Установите темы, которые отражены в софизме, предложенных преобразованиях
• Выясните, соблюдены ли все условия применимости теорем, правил, формул, соблюдена ли логичность. Некоторые софизмы построены на неверном использовании определений, законов, на «забывании» условий применимости. Очень часто в формулировках, правилах запоминаются основные, главные фразы и предложения, всё остальное упускается. И тогда второй признак равенства треугольников превращается в признак «по стороне и двум углам».
• Проверяйте результаты преобразования обратным действием.
• Часто следует разбить работу на небольшие блоки и проконтролировать правильность каждого такого блока.

А теперь перейдем к практике!

2+2=5

Чтобы доказать, что   2+2=5 , можно всего лишь доказать, что   4=5 Начнём с равенства: 16-36=25-45

Прибавим к обоим частям  20,25 , получим:

16-36+20,25=25-45+20,25

Заметим, что в обоих частях равенства можно вывести полный квадрат: 4²-2*4*4,5+4,5²=5²-2*5*4,5+4,5²

Преобразуем выражение:

(4-4,5)²=(5-4,5)²

Извлекаем корень из обоих частей равенства, получим: 4-4,5=5-4,5 4=5

Что и требовалось доказать.

Найдем ошибку в доказательстве

Извлечение корня не является равносильным преобразованием, поэтому правильное решение следующее: (4-4,5)²=(5-4,5)² Извлекаем корень и получаем:

Запомни!!  

a^2=b^2

a=+-b

При извлечении квадратного корня нарушено тождество

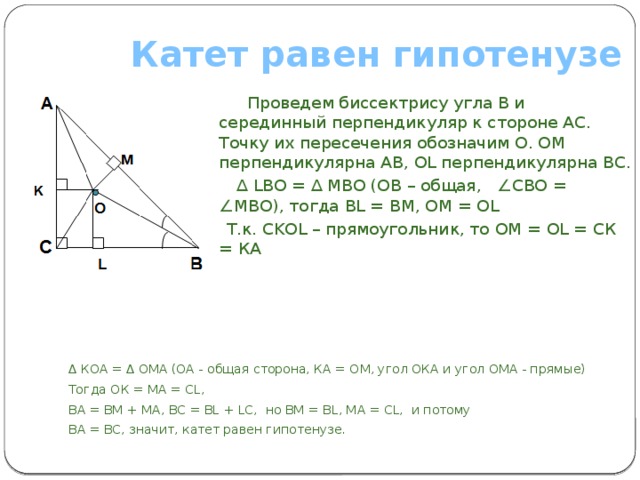
Катет равен гипотенузе

Проведем биссектрису угла В и серединный перпендикуляр к стороне АС. Точку их пересечения обозначим О. ОМ перпендикулярна АВ, ОL перпендикулярна ВС.

∆ LВО = ∆ МВО (ОВ – общая, ∠СВО = ∠МВО), тогда ВL = ВМ, ОМ = ОL

Т.к. CKOL – прямоугольник, то ОМ = ОL = СК = КА

По гипотенузе и острому углу

По гипотенузе и катету

∆ КОА = ∆ ОМА (ОА - общая сторона, КА = ОМ, угол ОКА и угол ОМА - прямые)

Тогда ОК = МА = СL,

ВА = ВМ + МА, ВС = ВL + LС, но ВМ = ВL, МА = СL, и потому

ВА = ВС, значит, катет равен гипотенузе.

Найдем ошибку в доказательстве

Ошибка в чертеже!

Серединный перпендикуляр к стороне и биссектриса противоположного ей угла для неравнобедренного треугольника, пересекаются вне этого треугольника

Спасибо за внимание 

Всегда будьте внимательны и не дайте себя обмануть!

Используемые источники информации:

Https://ru.wikipedia.org/wiki/%D0%A1%D0%BE%D1%8 4 %D0%B8%D0%B7%D0%BC

http://anadra.ru/sitemath/

http://festival.1september.ru/articles/313456/

Брадис В. М., Харчева А. К. Ошибки в математических рассуждениях. – М., 1938

Мадера А.Г., Мадера Д.А. Математические софизмы. – М.: Просвещение, 2003

Обреимов В. И. «Математические софизмы», 2-е изд., СПб., 1889г.