Проект по математике: " Математические софизмы"

Государственное бюджетное профессиональное образовательное учреждение Самарской области «Нефтегорский государственный техникум»

Тема: «Математические

софизмы»

ФИО студента: Топилин Евгений

Руководитель: Иванникова

Елена Станиславовна

Нефтегорск, 2017г.

Результаты анкетирования среди первых и вторых курсов

Анкета

1.ФИО

2.Группа, курс обучения

3.Знакомо ли вам понятие «Софизм»?

4.Надо ли знакомить учащихся на уроках с софизмами?

5.Хотел бы ты больше узнать о софизмах?

Цель :

Показать значимость математических софизмов при изучении математики, расширение математического кругозора.

Задачи:

1.Найти информацию, связанную с софизмами;

2.Выяснить виды софизмов;

3.Привести примеры софизмов;

4.Привести примеры типичных ошибок.

Софизм - формально кажущееся правильным, но по существу ложное умозаключение, основанное на неправильном подборе исходных положений (словарь Ожегова).

Математический софизм – удивительное утверждение, в доказательстве которого кроются незаметные, а подчас и довольно

тонкие ошибки.

Особенно часто в софизмах выполняют

«запрещенные» действия или не учитываются

условия применимости теорем, формул и правил.

Математические софизмы

геометрические

алгебраические

арифметические

В своей работе я рассмотрел

много математических софизмов

и сейчас приведу примеры

некоторых из них.

Алгебра — один из больших разделов математики, принадлежащий наряду с арифметикой и геометрией к числу старейших ветвей этой науки. Алгебраические софизмы – намеренно скрытые ошибки в уравнениях и числовых выражениях.

Решим систему двух уравнений:

Сделаем это подстановкой из второго уравнения в первое, получаем:

Уравнение можно записать как х+2у=8,

так что исходная система запишется в виде:

В этой системе уравнений коэффициенты при переменных одинаковы, а правые части не равны между собой, из этого следует, что система несовместна, т.е. не имеет ни одного решения. Перед тем, как решать систему линейных уравнений, полезно проанализировать, имеет ли система единственное решение, бесконечно

много решений или не имеет решений вообще.

Возьмём уравнение x - a =0. Разделим обе части уравнения на x - a ,получим

Любое равенство

можно делить только

на число, отличное от 0.

Арифметика - (греч. arithmetika, от arithmys — число), наука о числах, в первую очередь о натуральных (целых положительных) числах и (рациональных) дробях, и действиях над ними. Так что же такое арифметические софизмы?

Арифметические софизмы – это числовые выражения, имеющие неточность или ошибку, не заметную с первого взгляда.

Напишем тождество 4:4=5:5.

Вынесем из каждой части тождества общие множители за скобки, получаем: 4(1:1)=5(1:1) .

Так как 1:1=1, то сократим на 1 и получим 4 = 5, то есть 2*2=5

Ошибка сделана при вынесении общих множителей 4 из левой части и 5 из правой. Действительно, 4:4=1:1, но 4:4≠4(1:1).

Возьмём тождество

35+10-45=42+12-54.

В каждой части вынесем за скобки общий множитель:5(7+2-9)=6(7+2-9). Теперь получим, что 5=6.

Ошибка допущена при делении верного равенства 5(7+2-9)=6(7+2-9) на число 7+2-9, равное 0.Этого делать нельзя.

Любое равенство

можно делить только

на число, отличное от 0.

Это умозаключения или рассуждения, обосновывающие какую-нибудь заведомую нелепость, абсурд или противоречивое утверждение, связанное с геометрическими фигурами и действиями над ними

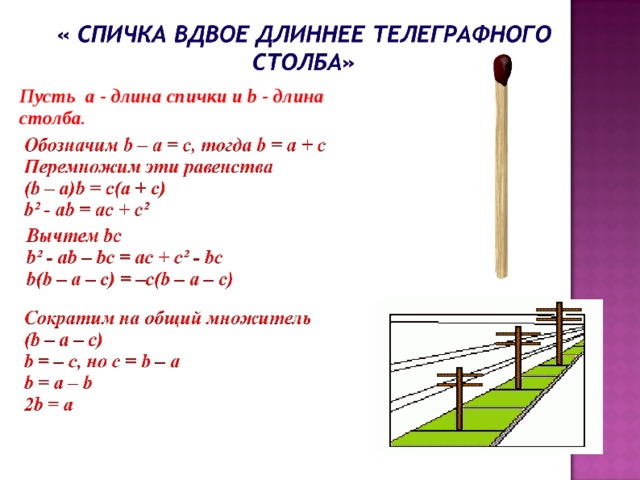
Пусть  а - длина спички и b - длина столба .

В выражении b(b-a-c )= -c(b-a-c) производится деление на (b-a-c), а этого делать нельзя, так как

b-a-c=0.Значит, спичка не может быть вдвое длиннее телеграфного столба.

Основные ошибки в софизмах: запрещенные действия, пренебрежение условиями теорем, формул и правил, ошибочный чертеж, опора на ошибочные умозаключения, деление на 0, неправильные выводы из равенства дробей; проведение преобразований над математическими объектами, не имеющими смысла.

• Приучают тщательно следить за точностью формулировок;
• Приучают ко внимательности при построении чертежей;
• Развивают логику и навыки правильного мышления

Я познакомился с увлекательной темой, узнал много нового, научился решать задачи на софизмы, находить в них ошибку.

Тема моей работы далеко не исчерпана. Я рассмотрел лишь некоторые, самые известные примеры софизмов . На самом деле их намного больше.

Развитая логика мышления поможет не только в решении каких-нибудь математических задач, но еще может пригодиться в жизни.