Проект учащихся 9 класса "Считать устно - легко"

Считать устно–легко

Подготовили

учащиеся 9 класса

Кубанской ош I-III ступеней

• Кузнецов Андрей
• Лещина Анастасия
• Плышевский Дмитрий
• Цюх Анастасия
• Велюллаева Алие
• Морбицр Владислав
• Кулиева Сабина
• Шарудилов Мирослав

Актуальность темы

• Устный счет – гимнастика для ума. Счет в уме является самым древним способом вычисления. Освоение вычислительных навыков развивает память и помогает усваивать предметы естественно-математического цикла.
• Существует много приемов упрощения арифметических действий. Знание упрощенных приемов вычисления особенно важно в тех случаях, когда вычисляющий не имеет в своем распоряжении таблиц и калькулятора.
• Мы хотим остановиться на способах сложения, вычитания, умножения, деления, для производства которых достаточно устного счета или применения ручки и бумаги.
• Мотивацией для выбора темы послужило желание продолжения формирования вычислительных навыков, умения быстро и чётко находить результат математических действий.
• Правила и приёмы вычислений не зависят от того, выполняются они письменно или устно. Однако, владение навыками устных вычислений представляет большую ценность не потому, что в быту ими пользуются чаще, чем письменными выкладкам и, а э то важно потому, что они ускоряют письменные вычисления, приобретают опыт рациональных вычислений, дают выигрыш в вычислительной работе.

Этапы работы над проектом:

• Организация двух групп
• Составление плана работы
• Распределение обязанностей
• Сбор и обработка информации
• Оформление результатов
• Защита проекта

Цели и задачи проекта

- Изучить способы быстрого (устного) счета.

-Отобрать самые актуальные и нужные .

-Рассказать о них в работе .

Основное назначение данного проекта – научиться применять приемы быстрого счета.

Изучить и научиться применять некоторые способы быстрого счета, для производства которых достаточно устного счета или применения ручки и бумаги.

Введение

• Современные ученики привыкли использовать калькулятор для более быстрого счета, но не всегда возможно и разрешено его использовать. Существует множество способов быстрого устного счета без калькулятора.
• Интерес данной темы заключается в том, что использование нестандартных приемов в формировании вычислительных навыков усиливает интерес учащихся к математике и содействует развитию математических способностей.
• Для того чтобы выяснить, знают ли современные школьники другие способы выполнения арифметических действий, кроме умножения, сложения, вычитания столбиком и деления «уголком» и хотели бы узнать новые способы, был проведен тестовый опрос и подведены итоги.

Итоги анкетирования

2) Перечисли, при изучении каких школьных предметов тебе понадобится правильно считать?

• 3)Знаешь ли ты приемы быстрого счета?

4)Применяешь ли ты при вычислениях приемы быстрого счета?

5) Хотели бы вы узнать приемы быстрого счета, чтобы быстро считать?

Интересный факт

•   Кто создал современную систему нумерации? Система счисления (система нумерации), которую мы сегодня знаем и используем, является заслугой индийского народа и ученых-математиков, которые изобрели системы счисления.  В I веке н. э. индийские ученые, на основе античной математики, создали привычную для нас сегодня десятичную позиционную систему. Для записи чисел они использовали 10 цифр, которые почти не изменились и до сегодня.

Счёт на пальцах

Способ быстрого умножения чисел в пределах первого десятка на 9.   Допустим, нам нужно умножить 7 на 9.

Повернём руки ладонями к себе и загнём седьмой палец (начиная считать от большого пальца слева).

Число пальцев слева от загнутого будет равно десяткам, а справа - единицам искомого произведения.

Умножение на однозначное число

• Когда одно из умножаемых чисел разлагается на однозначные множители, удобно бывает последовательно умножать на эти множители. Например: 225*6=225*2*3=450*3=1350

• Если оба множителя двузначные, мысленно разбивают один из них на десятки и единицы. Например:
• 29*12=29*10+29*2=290+58= 348
• 41*16=41*10+41*6 = 410+246 =656
• (или 41*16=16*41 = 16*40+16*1=640+16=656
• Разбивать на десятки и единицы выгоднее тот множитель, в котором они выражены меньшими числами.

Умножение на 9

• Чтобы устно умножить число на 9, приписывают к нему ноль и вычитают первый множитель. Например:
• 62*9=620-62=600—42=558
• 73*9=730-73=700—43=657

Умножение на 11

• Чтобы устно умножить число на 11, приписывают к нему н у ль и прибавляют первый множитель. Например:
• 87*11=870+87=957

Возведение в квадрат

• Чтобы воз вести в квадрат число, оканчивающееся цифрой 5 (например 85), умножают число десятков (8) на него же плюс единица (8*9=72) и приписывают 25 (в нашем примере получается 7225). Еще примеры:
• 25 2 ; 2*3=6; 625
• 45 2 ; 4*5= 20; 2025
• 145 2 ; 14*15 = 210; 21025

• Указанный прием применяется и к десятичным дробям, оканчивающимся цифрой 5:
• 8,5 2  = 72,25
• 14,5 2= 210,25
• 0,35 2  = 0,1225 

• Так как 0,5= 1/2 , а 0,25 = 1/4, то приведенным выше приемом можно пользоваться также и для воз веде ния в квадрат чисел, оканчивающихся дробью 1/2 :
• (8 1/2 ) 2  =72 1/4
• (14 1/2 ) 2  = 210 1/4

Умножение на 4

• Чтобы устно умножить число на 4, его дважды удваивают. Например:
• 112*4 = (112 *2 )*2 = 224*2= 448
• 335*4 = (335 *2 )*2 = 670*2= 1340

Деление на 4

• Чтобы устно разделить число на 4, его дважды делят пополам. Например:
• 76:4 = (76:2):2= 38:2=19
• 236:4= (236:2):2= 118:2=59

Умножение на 5

• Чтобы устно умножить число на 5 умножают его на 10/2, т. е. приписывают к числу н у ль и делят пополам. Например:
• 74*5= 740:2= 370
• 243*5=2430:2=1215
• При умножении на 5 четного числа удобнее сначала делить пополам и к полученному результату приписать н у ль. Например:
• 74X5 = 74/2*10=370

Умножение на 25

• Чтобы устно умножить число на 25, умножают его на 100/4 , т. е.—если число кратно 4- м —делят на 4 и к частному приписывают два н у ля.
• Например:
• 72*25 = 72/4*100= 1800
• Если же число при делении на 4 получается не целым, то запятую в частном переносим на два знака вправо.
• 65*25=65/4*100=16,25*100=1625

Старинные способы вычислений

• В России несколько веков назад среди крестьян некоторых губерний был распространен способ, который не требовал знание всей таблицы умножения. Надо было лишь уметь умножать и делить на 2. Этот способ получил название КРЕСТЬЯНСКИЙ.

РУССКИЙ КРЕСТЬЯНСКИЙ СПОСОБ УМНОЖЕНИЯ

• Пример: умножим 47 на 35,
• запишем числа на одной строке, проведём между ними вертикальную черту;
• левое число будем делить на 2, правое – умножать на 2 (если при делении возникает остаток, то остаток отбрасываем);
• деление заканчивается, когда слева появится единица;
• вычёркиваем те строки, в которых стоят слева чётные числа; 35 + 70 + 140 + 280 + 1120 = 1645
• далее оставшиеся справа числа складываем – это результат.

Еще один старинный метод

• Выдающийся арабский математик и астроном Абу Абдалах Мухаммед Бен Мусса аль – Хорезми жил и работал в Багдаде. Учёный работал в Доме мудрости, где были библиотека и обсерватория, здесь работали почти все крупные арабские учёные.
• Сведений о жизни и деятельности Мухаммеда аль – Хорезми очень мало. Сохранились лишь две его работы – по алгебре и по арифметике. В последн е й из этих книг даны четыре правила арифметических действий, почти такие же, что используются в наше время.
• В своей «Книге об индийском счете» учёный описал способ, придуманный в Древней Индии, а позже названный «МЕТОДОМ РЕШЁТКИ» . Этот метод даже проще, чем применяемый сегодня.

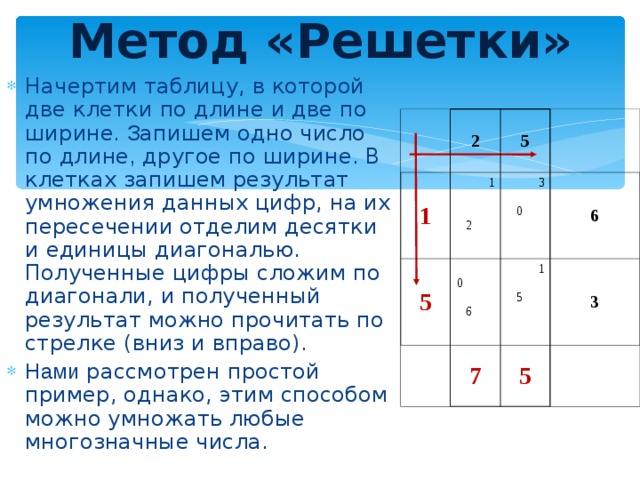
Метод «Решетки»

• Начертим таблицу, в которой две клетки по длине и две по ширине . З апишем одно число по длине , другое по ширине. В клетках запишем результат умножения данных цифр, на их пересечении отделим десятки и единицы диагональю. Полученные цифры сложим по диагонали, и полученный результат можно прочитать по стрелке (вниз и вправо).
• Нами рассмотрен простой пример, однако, этим способом можно умножать любые многозначные числа.

2

1

1

2

5

5

0

6

3

0

6

7

1

5

3

5

Различные способы сложения и вычитания

1)СЛОЖЕНИЕ

• Основное правило для выполнения сложения в уме звучит так: Чтобы прибавить одно число к числу 9, прибавьте к нему 10 и отнимите 1; чтобы прибавить 8, прибавьте 10 и отнимите 2; чтобы прибавить 7, прибавьте10 и отнимите 3 и т.д.
• Например:

56+8=56+10-2=64;

65+9=65+10-1=74.

2) СЛОЖЕНИЕ В УМЕ ДВУЗНАЧНЫХ ЧИСЕЛ

• Если цифра единиц в прибавляемом числе больше 5, то число необходимо округлить в сторону увеличения, а затем вычесть ошибку округления из полученной суммы. Если же цифра единиц меньше чем 5, то прибавляем сначала десятки, а потом единицы.
• Например:

34+48=34+50-2=82;

27+31=27+30+1=58.

3 )СЛОЖЕНИЕ ТРЕХЗНАЧНЫХ ЧИСЕЛ

• Складываем слева направо, то есть сначала сотни, потом десятки, а затем единицы. Например:

359+523= 300+500+50+20+9+3=882;

456+298=400+200+50+90+6+8=754.

4 )ВЫЧИТАНИЕ

• Чтобы вычесть два числа в уме, нужно округлить вычитаемое, а затем подкорректир овать полученный ответ.

56-9=56-10+1=47;

436-87=436-100+13=349.

5) ВЫЧИТАНИЕ ЧИСЛА МЕНЬШЕ 100 ИЗ ЧИСЛА БОЛЬШЕ 100

• Если вычитаемое меньше 100 , а уменьшаемое больше 100 , но меньше 200 , есть простой способ вычислить разность в уме.
• Например:

• Найдем разность чисел 134 и 76

134-76=..

76 на 24 меньше 100 . 134 на 34 больше 100 . Прибавим 24 к 34 и получим ответ: 58 .

134-76=24+34=58

• Найдем разность чисел 152 и 88

152-88=..

88 на 12 меньше 100 , а 152 больше 100 на 52 , значит к 12 прибавим 52

152-88=12+52=64

Вычитание из 1000

• Чтобы выполнить вычитание из 1000, може м пользоваться этим простым правилом:

Отнимите от 9 все цифры, кроме последней. А последнюю цифру отнимите от 10 :

1000-648

• Шаг1: от 9 отнимите 6 = 3 Шаг2: от 9 отнимите 4 = 5 Шаг3: от 10 отнимите 8 = 2 Ответ: 352

• И, напоследок, математический трюк:
• Возведение во вторую степень чисел: 11,111,1111,11111…

Закономерность такова: Если взять за основу бесконечный ряд натуральных чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 ..и т. д., то при возведении в квадрат чисел из х единиц (111111...и так х раз!), получается зеркально симметричное число, состоящее из двух частей. Первая часть есть числа натурального ряда от 1 до х , а зеркальная часть - в обратном порядке, начиная с полученного числа х .

Выводы:

•   Существуют способы быстрого сложения, вычитания, умножения, деления, возведения в степень …Мы рассмотрели лишь немногие способы быстрого счета.
• Все рассмотренные нами методы устного вычисления говорят о многолетнем интересе ученых и простых людей к игре с цифрами. Используя некоторые из этих методов на уроках или дома можно развить скорость вычислений, добиться успехов в изучении всех школьных предметов.
• Умножение без калькулятора – тренировка памяти и математического мышления. Вычислительная техника совершенствуется и по сей день, но любая машина делает то, что в нее закладывают люди, а мы узнали некоторые приемы устного счета, которые помогут нам в жизни.
• Нам было интересно работать над проектом. Пока мы только изучали и анализировали уже известные способы быстрого счета.
• Но кто знает, возможно, в будущем мы сами сможем открыть новые способы быстрых вычислений.

Устный счёт – гимнастика ума.

Умеете ли вы считать? Каждый, конечно ответит: «Да!»

СПАСИБО ЗА ВНИМАНИЕ!