
Пояснительная записка
Рабочая программа составлена на основе нормативных документов:
- Федеральный компонент государственного образовательного стандарта начального общего основного общего и среднего (полного) общего образования (Приказ МОРФ от 05.03.2004 №1085)
- Федерального закона «Об образовании в Российской Федерации»
от 29 декабря 2012 года №273-ФЗ;
- приказа Министерства образования Российской Федерации от 5 марта 2004 г. № 1089 «Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования» (с изменениями);
- приказа Министерства образования Российской Федерации от 9 марта 2004 г. № 1312 «Об утверждении федерального базисного учебного плана и примерных учебных планов для образовательных учреждений РФ, реализующих программы общего образовании» (с изменениями);
- приказа Минобрнауки России от 30 августа 2013 года № 1015 «Об утверждении Порядка организации и осуществления образовательной деятельности по основным общеобразовательным программам - образовательным программам начального общего, основного общего и среднего общего образования»;
- Письмом департамента образования и науки Брянской области от 13.04.2016г. № 2610-04-0 «О примерном учебном плане 5-9 классов общеобразовательных организаций Брянской области на 2016-2017 учебный год»
-Постановлением Главного государственного санитарного врача РФ от 29.12.2010 № 189 « Об утверждении СанПин 2.4.2.2821-10 «Санитарно-эпидемиологические требования к условиям и организации обучения в общеобразовательных учреждениях», зарегистрированного в Минюсте России 03.03.2011, регистрационный номер 19993) (с изменениями идополнениями, внесенными Постановлениями Главного государственного санитарного врача РФ от 29 июня 2011г., 25 декабря 2013г., 24 ноября 2015 года).
- Уставом МБОУ Летошницкой СОШ в целях обеспечения единого образовательного пространства.
-Программы общеобразовательных учреждений. Алгебра. 7-9 классы. Составитель Бурмистрова Т.А. Авторы программы Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова. 3-е изд. М.: Просвещение, 2010
- Программы общеобразовательных учреждений. Геометрия. 7-9 классы. Программа по геометрии. Авторы программы Л.С.Атанасян, В.Ф. Бутузов, С.Б. Кадомцев. Составитель Бурмистрова Т.А. 3-е изд. М.:Просвещение, 2010.
Согласно базисному учебному плану на изучение математики в 8 классе отводится 5 часов в неделю из них на изучение алгебры 3 часа в неделю, всего 105 часа и на изучение геометрии 2 часа в неделю, всего -70 часов. Рабочая программа рассчитана на 175 часов.
1.«Алгебра 8 класс» авторы Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.В. Суворова. Москва, «Просвещение» 2010г. 2. «Геометрия, 7 - 9» авторы Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. М.: Просвещение, 2009г.
Цели изучения курса математики в 8 классе:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей, принятию самостоятельных решений;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
Изучение математики в 8 классе направлено на решение следующих задач:
развитие вычислительных и формально-оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных дисциплин (физика, химия, информатики);
усвоение аппарата уравнений и неравенств как основного средства математического моделирования прикладных задач;
осуществление функциональной подготовки школьников;
формирование умения переводить практические задачи на язык математики.
формирование умения воспринимать и анализировать информацию, представленную в различных формах;
обогащение представлений о современной картине мира и методах его исследования;
формирование понимания роли статистики как источника социально значимой информации.
Общая характеристика учебного предмета.
Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.
Арифметика призвана способствовать приобретению практических навыков, необходимых для повседневной жизни. Она служит базой для всего дальнейшего изучения математики, способствует логическому развитию и формированию умения пользоваться алгоритмами.
Изучение курса алгебры нацелено на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира (одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у обучающихся представлений о роли математики в развитии цивилизации и культуры.
Геометрия — один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания обучающихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчёты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчёт числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.
Таким образом, в ходе освоения содержания курса учащиеся получают возможность:
развить представление о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Предмет «Математика» в 7-9 классах состоит из разделов «Алгебра» и «Геометрия». Раздел «Алгебра» включает некоторые вопросы арифметики, развивающие числовую линию 5-6 классов, собственно алгебраический материал, простейшие элементарные функции, в том 7 числе и квадратный корень, а также содержит новое направление, отражающее элементы теории вероятностей и математической статистики. Раздел «Геометрия» традиционно изучает евклидову геометрию, элементы векторной алгебры, геометрические преобразования, а также содержит элементы неевклидовой сферической геометрии и элементы неевклидовой геометрии Лобачевского. Элементы логики и комбинаторики систематически включаются в содержание учебного материала с 5 по 8 класс. В 9 классе предполагается изучение данного материала, включающее в себя изучение основных правил комбинаторики и знакомство с основными элементарными задачами комбинаторики. Новый для школы вероятностно-статистический материал с 5 по 8 класс ограничивается представлением результатов измерений в виде таблиц или диаграмм. Систематическое изучение элементов теории вероятностей и математической статистики предлагается начинать с 9 класса знакомством с понятиями эксперимента со случайными исходами, событиями и вероятностью событий, с учетом последующего изучения и углубления в старших классах. Система вопросов и заданий в курсе математики 5-9 классов позволяет учитывать возрастные и психологические особенности обучающихся, а также их индивидуальные интересы. Задачи и задания способствуют развитию критического мышления, овладению приемами анализа, синтеза, отбора и систематизации материала, формируют умение учиться и организовывать свою деятельность. Система тестовых заданий позволяет выявить степень усвоения изученного материала.
Описание места учебного предмета «Математика» в учебном плане.
В соответствии с требованиями Федерального государственного образовательного стандарта основного общего образования предмет «Математика» изучается с 5-го по 9-й класс в виде следующих учебных курсов: 5–6 класс – «Математика», 7–9 класс – «Алгебра» и «Геометрия». Общее количество уроков в неделю с 5 по 9 класс составляет 875 часов (5–6 класс – по 5 часов в неделю (170 часов), 7–9 класс – алгебра по 3 часа в неделю (105 часов), геометрия – по 2 часа в неделю (70 часов).)
| Количество контрольных работ по алгебре | 10 |
| Количество контрольных работ по геометрии | 6 |
Содержание учебного предмета, курса
Курс алгебры 8-го класса состоит из 6 тем:
Глава 1. Рациональные дроби (23 часа)
Рациональная дробь. Основное свойство дроби, сокращение дробей. Тождественные преобразования рациональных выражений. Функция у =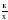 и её график.
и её график.
Цель: выработать умение выполнять тождественные преобразования рациональных выражений.
Так как действия с рациональными дробями существенным образом опираются на действия с многочленами, то в начале темы необходимо повторить с обучающимися преобразования целых выражений.
Главное место в данной теме занимают алгоритмы действий с дробями. Учащиеся должны понимать, что сумму, разность, произведение и частное дробей всегда можно представить в виде дроби. Приобретаемые в данной теме умения выполнять сложение, вычитание, умножение и деление дробей являются опорными в преобразованиях дробных выражений. Поэтому им следует уделить особое внимание. Нецелесообразно переходить к комбинированным заданиям на все действия с дробями прежде, чем будут усвоены основные алгоритмы. Задания на все действия с дробями не должны быть излишне громоздкими и трудоемкими.
При нахождении значений дробей даются задания на вычисления с помощью калькулятора. В данной теме расширяются сведения о статистических характеристиках. Вводится понятие среднего гармонического ряда положительных чисел.
Изучение темы завершается рассмотрением свойств графика функции у =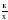 .
.
Глава 2. Квадратные корни (19 часов)
Понятие об иррациональных числах. Общие сведения о действительных числах. Квадратный корень. Понятие о нахождении приближенного значения квадратного корня. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни. Функция у = 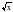 , её свойства и график.
, её свойства и график.
Цель: систематизировать сведения о рациональных числах и дать представление об иррациональных числах, расширив тем самым понятие о числе; выработать умение выполнять преобразования выражений, содержащих квадратные корни.
В данной теме учащиеся получают начальное представление о понятии действительного числа. С этой целью обобщаются известные обучающимся сведения о рациональных числах. Для введения понятия иррационального числа используется интуитивное представление о том, что каждый отрезок имеет длину и потому каждой точке координатной прямой соответствует некоторое число. Показывается, что существуют точки, не имеющие рациональных абсцисс.
При введении понятия корня полезно ознакомить обучающихся с нахождением корней с помощью калькулятора.
Основное внимание уделяется понятию арифметического квадратного корня и свойствам арифметических квадратных корней. Доказываются теоремы о корне из произведения и дроби, а также тождество 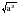 =
=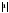 , которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида
, которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида 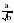 ,
, 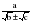 . Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа.
. Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа.
Продолжается работа по развитию функциональных представлений обучающихся. Рассматриваются функция у=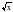 , её свойства и график. При изучении функции у=
, её свойства и график. При изучении функции у=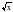 , показывается ее взаимосвязь с функцией у = х2, где х ≥ 0.
, показывается ее взаимосвязь с функцией у = х2, где х ≥ 0.
Глава 3. Квадратные уравнения (21 часа)
Квадратное уравнение. Формула корней квадратного уравнения. Решение рациональных уравнений. Решение задач, приводящих к квадратным уравнениям и простейшим рациональным уравнениям.
Цель: выработать умения решать квадратные уравнения и простейшие рациональные уравнения и применять их к решению задач.
В начале темы приводятся примеры решения неполных квадратных уравнений. Этот материал систематизируется. Рассматриваются алгоритмы решения неполных квадратных уравнений различного вида.
Основное внимание следует уделить решению уравнений вида ах2 + bх + с = 0, где, а  0, с использованием формулы корней. В данной теме учащиеся знакомятся с формулами Виета, выражающими связь между корнями квадратного уравнения и его коэффициентами. Они используются в дальнейшем при доказательстве теоремы о разложении квадратного трехчлена на линейные множители.
0, с использованием формулы корней. В данной теме учащиеся знакомятся с формулами Виета, выражающими связь между корнями квадратного уравнения и его коэффициентами. Они используются в дальнейшем при доказательстве теоремы о разложении квадратного трехчлена на линейные множители.
Учащиеся овладевают способом решения дробных рациональных уравнений, который состоит в том, что решение таких уравнений сводится к решению соответствующих целых уравнений с последующим исключением посторонних корней.
Изучение данной темы позволяет существенно расширить аппарат уравнений, используемых для решения текстовых задач.
Глава 4. Неравенства (20 часов)
Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Погрешность и точность приближения. Линейные неравенства с одной переменной и их системы.
Цель: ознакомить обучающихся с применением неравенств для оценки значений выражений, выработать умение решать линейные неравенства с одной переменной и их системы.
Свойства числовых неравенств составляют ту базу, на которой основано решение линейных неравенств с одной переменной. Теоремы о почленном сложении и умножении неравенств находят применение при выполнении простейших упражнений на оценку выражений по методу границ. Вводятся понятия абсолютной Погрешности и точности приближения, относительной погрешности.
Умения проводить дедуктивные рассуждения получают развитие, как при доказательствах указанных теорем, так и при выполнении упражнений на доказательства неравенств.
В связи с решением линейных неравенств с одной переменной дается понятие о числовых промежутках, вводятся соответствующие названия и обозначения. Рассмотрению систем неравенств с одной переменной предшествует ознакомление обучающихся с понятиями пересечения и объединения множеств.
При решении неравенств используются свойства равносильных неравенств, которые разъясняются на конкретных примерах. Особое внимание следует уделить отработке умения решать простейшие неравенства вида ах b, ах b, остановившись специально на случае, когда, а0.
В этой теме рассматривается также решение систем двух линейных неравенств с одной переменной, в частности таких, которые записаны в виде двойных неравенств.
Глава 5. Степень с целым показателем. Элементы статистики (11 часов)
Степень с целым показателем и ее свойства. Стандартный вид числа. Начальные сведения об организации статистических исследований.
Цель: выработать умение применять свойства степени с целым показателем в вычислениях и преобразованиях, сформировать начальные представления о сборе и группировке статистических данных, их наглядной интерпретации.
В этой теме формулируются свойства степени с целым показателем. Метод доказательства этих свойств показывается на примере умножения степеней с одинаковыми основаниями. Дается понятие о записи числа в стандартном виде. Приводятся примеры использования такой записи в физике, технике и других областях знаний.
Учащиеся получают начальные представления об организации статистических исследований. Они знакомятся с понятиями генеральной и выборочной совокупности. Приводятся примеры представления статистических данных в виде таблиц частот и относительных частот. Обучающимся предлагаются задания на нахождение по таблице частот таких статистических характеристик, как среднее арифметическое, мода, размах. Рассматривается вопрос о наглядной интерпретации статистической информации. Известные обучающимся способы наглядного представления статистических данных с помощью столбчатых и круговых диаграмм расширяются за счет введения таких понятий, как полигон и гистограмма.
6. Повторение (8 часов)
Цель: Повторение, обобщение и систематизация знаний, умений и навыков за курс алгебры 8 класса.
Курс геометрии 8-го класса состоит из 4 тем:
Четырехугольники (14ч)
Основная цель – изучить наиболее важные виды четырехугольников – параллелограмм, прямоугольник, ромб, квадрат, трапецию; дать представление о фигурах, обладающих осевой или центральной симметрией.
2.Площадь (14ч)
Основная цель – расширить и углубить полученные в 5-6 классах представления учащихся об измерении и вычислении площадей; вывести формулы площадей прямоугольника, параллелограмма, треугольника, трапеции; доказать одну из главных теорем геометрии – теорему Пифагора.
3. Подобные треугольники (19ч)
Основная цель – ввести понятие подобных треугольников; рассмотреть признаки подобия треугольников и их применения; сделать первый шаг в освоении учащимися тригонометрического аппарата геометрии.
Признаки подобия треугольников. Соотношения между сторонами и углами прямоугольного треугольника. Основное тригонометрическое тождество. Формулы, связывающие синус, косинус, тангенс, котангенс одного и того же угла. Теорема косинусов и теорема синусов; примеры их применения для вычисления элементов треугольника.
4. Окружность (17ч)
основная цель – расширить сведения об окружности, полученные учащимися в 7 классе; изучить новые факты, связанные с окружностью; познакомить учащихся с четырьмя замечательными точками треугольника.
Центр, радиус, диаметр. Дуга, хорда. Центральный, вписанный угол; величина вписанного угла. Взаимное расположение прямой и окружности, двух окружностей. Касательная и секущая к окружности; равенство касательных, проведенных из одной точки. Метрические соотношения в окружности: свойства секущих, касательных, хорд.
Окружность, вписанная в треугольник, и окружность, описанная около треугольника. Вписанные и описанные четырехугольники. Вписанные и описанные окружности правильного многоугольника.
Повторение. Решение задач.(4)
Планирование учебного материала
| № | Содержание материала | Количество часов |
|
| Алгебра |
|
| 1 | Глава I. Рациональные дроби | 23 |
| 2 | Глава II. Квадратные корни | 19 |
| 3 | Глава III. Квадратные уравнения | 21 |
| 4 | Глава IV. Неравенства | 20 |
| 5 | Глава V. Степень с целым показателем. Элементы статистики | 11 |
| 6 | Повторение | 8 |
|
| Резерв | 3 |
|
|
| 105 |
|
| Геометрия |
|
| 7 | Четырехугольники | 14 |
| 8 | Площадь | 14 |
| 9 | Подобные треугольники | 19 |
| 10 | Окружность | 17 |
| 11 | Повторение | 4 |
|
| Резерв | 2 |
|
|
| 70 |
Описание материально технического обеспечения образовательного процесса.
Для реализации целей и задач обучения математике по данной программе используется УМК по математике для 8 класса:
1.Атанасян Л.С., Бутузов В.Ф. и др - Геометрия: учеб. Для 7-9 кл. срд. шк./ М.: Просвещение, 2007
2. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др./ Под ред. Теляковского С.А. Алгебре. 8 класс: учеб. / М. Просвещение, 2007.
3.Геометрия 7-9 классы. Программы общеобразовательных учреждений/ М.: Просвещение 2009
4.Жохов В.И. и др. Алгебра. Дидактические материалы для 8 класса.
5.Макарычев Ю.Н. и др. Алгебра. Дидактические материалы для 8 класса.
6.Жохов В.И. и др. Уроки алгебры в 7, 8 и 9 классах. Поурочные разработки.
7.Гилярова М. Г. Поурочные разработки по геометрии: 8 класс-2 изд., Волгоград
8.О. Н. Пирютко, Н. Н. Рачковский, Е. Т. Гуреев. Тесты. Алгебра. 8 класс./ Минск.
К техническим средствам обучения, которые могут эффективно использоваться на уроках математики, относятся компьютер, цифровой фотоаппарат и др. Перечень работ при использовании компьютера: –поиск дополнительной информации в Интернете; – создание текста доклада; – обработка данных проведенных математических исследований; – создание мультимедийных презентаций (текстов с рисунками, фотографиями и т.д.), в том числе для представления результатов исследовательской и проектной деятельности. При использовании компьютера учащиеся применяют полученные на уроках информатики инструментальные знания (например, умения работать с текстовыми, графическими редакторами и т.д.), тем самым у них формируется готовность и привычка к практическому применению новых информационных технологий. Технические средства на уроках математики широко привлекаются также при подготовке проектов (компьютер).
Требования к уровню подготовки учащихся
В результате изучения математики ученик должен
знать/понимать
-существо понятия математического доказательства; примеры доказательств;
-существо понятия алгоритма; примеры алгоритмов;
-как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
-как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
-как потребности практики привели математическую науку к необходимости расширения понятия числа;
-вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
-каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
-смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
В результате изучения алгебры ученик должен
знать/понимать
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
уметь
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним;
решать линейные неравенства с одной переменной и их системы;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами.
В результате изучения геометрии ученик должен
уметь
пользоваться языком геометрии для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;
распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;
в простейших случаях строить сечения и развертки пространственных тел;
проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами;
вычислять значения геометрических величин (длин, углов, площадей, объемов), в том числе: для углов от 0 до 180 определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, идеи симметрии;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
решать простейшие планиметрические задачи в пространстве;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
описания реальных ситуаций на языке геометрии;
расчетов, включающих простейшие тригонометрические формулы;
решения геометрических задач с использованием тригонометрии
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).
Тематическое планирование алгебра 8 класс
| № урока | Изучаемый материал | кол-во часов | Дата по плану | Дата фактическая | Требования к уровню подготовки уч-ся |
| 1
2 | Повторение. Преобразование целых выражений. Повторение. Преобразование целых выражений | 1
1 |
|
|
|
| 3 | Рациональные выражения | 1 |
|
| Выработать умение выполнять тождественные преобразования рациональных выражений. Вычислять значение дробного алгебраического выражения. Определять, находить допустимые значения переменных, находить наименьший общий знаменатель, сокращать дроби, приводить дроби к наименьшему общему знаменателю, выполнять сложение, вычитание, умножение и деление дробей, упрощать рациональные выражения, представлять рациональные выражения в виде дроби, доказывать тождества, рисовать, изображать график обратной пропорциональности, упрощать рациональные выражения, путем их тождественных преобразований. |
| 4 | Рациональные выражения и их свойства | 1 |
|
|
| §2. Сумма и разность дробей – 9ч. |
|
|
| 5 | Основное свойство дроби. Сокращение дробей. | 1 |
|
|
| 6 | Основное свойство дроби. Сокращение дробей. | 1 |
|
|
| 7 | Сложение дробей с одинаковыми знаменателями. | 1 |
|
|
| 8 | Вычитание дробей с одинаковыми знаменателями. | 1 |
|
|
| 9 | Сложение и вычитание дробей с одинаковыми знаменателями. | 1 |
|
|
| 10 | Сложение дробей с разными знаменателями. | 1 |
|
|
| 11 | Вычитание дробей с разными знаменателями. | 1 |
|
|
| 12 | Сложение и вычитание дробей с разными знаменателями. | 1 |
|
|
| 13 | Решение задач | 1 |
|
|
| 14 | Контрольная работа №1 | 1 |
|
|
| §3. Произведение и частное дробей – 10ч. |
|
| 15 | Умножение дробей. Возведение дроби в степень | 1 |
|
|
| 16 | Умножение дробей. Возведение дроби в степень | 1 |
|
|
| 17 | Деление дробей | 1 |
|
|
| 18 | Деление дробей | 1 |
|
|
| 19 | Преобразование рациональных выражений | 1 |
|
|
| 20 | Преобразование рациональных выражений | 1 |
|
|
| 21 | Преобразование рациональных выражений | 1 |
|
|
| 22 | Функция 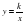 и ее график и ее график | 1 |
|
|
| 23 | Функция 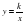 и ее график и ее график | 1 |
|
|
| 24 | Решение задач. | 1 |
|
|
| 25 | Контрольная работа №2 | 1 |
|
|
| 26 | Рациональные числа | 1 |
|
|
|
| 27 | Иррациональные числа | 1 |
|
| Систематизировать сведения о рациональных числах и дать представление об иррациональных числах, выработать умение выполнять простейшие преобразования выражений, содержащих квадратные корни. Вычислять, находить значения числовых выражений, содержащих квадратные корни; упрощать выражения, содержащие квадратные корни; находить приближенные значение квадратного корня; решать квадратные уравнения вида х2 = а; рисовать по трем точкам график квадратного корня; находить область определения выражений, содержащие дроби и квадратные корни; упрощать выражения путем вынесения множителя из под знака квадратного корня; путем внесения множителя под знак квадратного корня; сравнивать значения выражений, содержащие квадратные корни, использование свойство возраст. корня, доказывать, определять рациональные и иррациональные выражения. |
| §5. Арифметический квадратный корень – 5ч. |
|
| 28 | Квадратные корни. Арифметический квадратный корень | 1 |
|
|
| 29 | Уравнение х2 = а | 1 |
|
|
| 30 | Нахождение приближенных значений квадратного корня | 1 |
|
|
| 31 | Функция 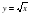 и её график и её график | 1 |
|
|
| 32 | Решение задач по теме «Арифметический квадратный корень» | 1 |
|
|
| §6. Свойства арифметического квадратного корня – 3ч. |
|
| 33 | Квадратный корень из произведения и дроби | 1 |
|
|
| 34 | Квадратный корень из степени | 1 |
|
|
| 35 | Решение задач | 1 |
|
|
| 36 | Контрольная работа №3 | 1 |
|
|
| §7. Применение свойств арифметического квадратного корня – 7ч. |
|
| 37 | Вынесение множителя за знак корня. | 1 |
|
|
| 38 | Внесение множителя под знак корня | 1 |
|
|
| 39 | Решение задач | 1 |
|
|
| 40 | Преобразование выражений, содержащих квадратные корни | 1 |
|
|
| 41 | Преобразование выражений, содержащих квадратные корни | 1 |
|
|
| 42 | Преобразование выражений, содержащие квадратные корни | 1 |
|
|
| 43 | Решение задач | 1 |
|
|
| 44 | Контрольная работа №4 | 1 |
|
|
| 45 | Неполные квадратные уравнения | 1 |
|
| Выработать умение решать квадратные уравнения и применять их к решению задач. Сформировать представление о множестве действительных чисел, научить решать неполные квадратные уравнения; выделять из трехчлена квадрат двухчленна; решать уравнения с помощью формулы; применять формулы нахождения дискриминанта и корней квадратного уравнения; научить составлять уравнения по условию задачи и определять, соответствуют ли найденные корни уравнения условию задачи; установить связь между геометрией и алгеброй; «открыть» зависимость между корнями уравнения и его коэффициентами; научить применять теорему Виета и обратную ей теорему при решении квадратных уравнений. |
| 46 | Неполные квадратные уравнения | 1 |
|
|
| 47 | Формула корней квадратного уравнения | 1 |
|
|
| 48 | Формула корней квадратного уравнения | 1 |
|
|
| 49 | Решение задач | 1 |
|
|
| 50 | Решение задач с помощью квадратных уравнений | 1 |
|
|
| 51 | Решение задач с помощью квадратных уравнений | 1 |
|
|
| 52 | Теорема Виета | 1 |
|
|
| 53 | Теорема Виета | 1 |
|
|
| 54 | Решение задач | 1 |
|
|
| 55 | Контрольная работа №5 | 1 |
|
|
| §9. Дробные рациональные уравнения – 9ч. |
|
| 56 | Решение дробных рациональных уравнений | 1 |
|
|
| 57 | Решение дробных рациональных уравнений | 1 |
|
|
| 58 | Решение дробных рациональных уравнений | 1 |
|
|
| 59 | Решение задач по теме | 1 |
|
|
| 60 | Решение задач с помощью рациональных уравнений | 1 |
|
|
| 61 | Решение задач с помощью рациональных уравнений | 1 |
|
|
| 62 | Решение задач с помощью рациональных уравнений | 1 |
|
|
| 63 | Решение задач | 1 |
|
|
| 64 | Решение задач | 1 |
|
|
| 65 | Контрольная работа №6 | 1 |
|
|
| 66 | Числовые неравенства | 1 |
|
| Выработать умение решать линейные неравенства с одной переменной и их системы; научить использовать определения (ав, если а – в 0) для доказательства неравенств; для сравнения чисел; применять свойства неравенства при решении неравенств; иллюстрировать эти свойства на координатной прямой; записывать в виде промежутков, с помощью обозначений; сформировать умение решать линейные неравенства с одной переменной; системы неравенств; сводить систему неравенств к системе линейных неравенств. |
| 67 | Числовые неравенства | 1 |
|
|
| 68 | Свойства числовых неравенств | 1 |
|
|
| 69 | Свойства числовых неравенств | 1 |
|
|
| 70 | Сложение числовых неравенств | 1 |
|
|
| 71 | Умножение числовых неравенств | 1 |
|
|
| 72 | Погрешность и точность приближения | 1 |
|
|
| 73 | Решение задач | 1 |
|
|
| 74 | Контрольная работа №7 | 1 |
|
|
| §11. Неравенства с одной переменной и их системы – 10ч. |
|
| 75 | Пересечение и объединение множеств | 1 |
|
|
| 76 | Числовые промежутки | 1 |
|
|
| 77 | Числовые промежутки | 1 |
|
|
| 78 | Решение неравенств с одной переменной | 1 |
|
|
| 79 | Решение неравенств с одной переменной | 1 |
|
|
| 80 | Решение задач | 1 |
|
|
| 81 | Решение систем неравенств с одной переменной | 1 |
|
|
| 82 | Решение систем неравенств с одной переменной | 1 |
|
|
| 83 | Решение систем неравенств с одной переменной | 1 |
|
|
| 84 | Решение задач | 1 |
|
|
|
| 85 | Контрольная работа №8 | 1 |
|
|
| 86 | Определение степени с целым отрицательным показателем | 1 |
|
| Сформировать умение выполнять действия над степенями с целыми показателями, ввести понятие стандартного вида числа; выработать умение работать со степенями, применять свойства степени; научиться указывать верные цифры в записи приближенного значения числа; применять правила работы с приближенными значениями. |
| 87 | Определение степени с целым отрицательным показателем | 1 |
|
|
| 88 | Свойства степени с целым показателем | 1 |
|
|
| 89 | Свойства степени с целым показателем | 1 |
|
|
| 90 | Стандартный вид числа | 1 |
|
|
| 91 | Решение задач | 1 |
|
|
| 92 | Контрольная работа №9 | 1 |
|
|
| §13. Элементы статистики – 4ч. |
|
| 93 | Сбор статистических данных | 1 |
|
|
|
| 94 | Группировка статистических данных | 1 |
|
|
|
| 95 | Наглядное представление статистической информации | 1 |
|
|
|
| 96 | Решение задач | 1 |
|
|
|
| Повторение – 9ч. |
|
|
|
| 97 | Рациональные дроби и действия над ними | 1 |
|
|
|
| 98 | Рациональные дроби и действия над ними | 1 |
|
|
|
| 99 | Преобразование выражений, содержащих квадратные корни | 1 |
|
|
|
| 100 | Квадратные уравнения | 1 |
|
|
|
| 101-102 | Итоговая контрольная работа | 2 |
|
|
|
| 103 | Анализ итоговой контрольной работы | 1 |
|
|
|
| 104-105 | Резерв | 2 |
|
|
|
Тематическое планирование геометрия 8
| № урока | Изучаемый материал | кол-во часов | Дата по плану | Дата фактическая | Требования к уровню подготовки уч-ся |
| 1
2 | Вводное повторение. Треугольники.
Вводное повторение. Соотношение между сторонами и углами треугольника. | 1
1
|
|
|
|
| 3 | §1. Многоугольники. | 1 |
|
| Формировать понятие «многоугольника». Научить находить сумму углов n – угольника, периметр n-угольника |
| 4 | Многоугольники. Решение задач. | 1 |
|
|
| 5 | §2. Параллелограмм. | 1 |
|
| Св-ва и признаки параллелограмма, их применение при решении задач, решение задач на построение. |
| 6 | Признаки параллелограмма. | 1 |
|
|
| 7 | Решение задач по теме «Параллелограмм» | 1 |
|
|
| 8 | Трапеция. | 1 |
|
|
| 9 | Теорема Фалеса. | 1 |
|
|
| 10 | Задачи на построение | 1 |
|
|
| 11 | §3. Прямоугольник. | 1 |
|
| Св-ва прямоугольника, ромба, квадрата и их применение при решении задач; строить симметричные точки и распознавать фигуры, обладающие осевой и центральной симметрией. Закрепить изученный материал. Проконтролировать знания уч-ся |
| 12 | Ромб. Квадрат. | 1 |
|
|
| 13 | Решение задач | 1 |
|
|
| 14 | Осевая и центральная симметрии | 1 |
|
|
| 15 | Решение задач | 1 |
|
|
| 16 | Контрольная работа №1 по теме «Четырехугольники» | 1 |
|
|
| 17 | §1. Площадь многоугольника. | 1 |
|
| Понятие площади многоугольника, св-ва площадей, единицы измерения. |
| 18 | Площадь многоугольника. | 1 |
|
|
| 19 | §2. Площадь параллелограмма. | 1 |
|
| Умение доказывать теоремы и находить площади параллелограмма,  и трапеции. и трапеции. |
| 20 | Площадь треугольника | 1 |
|
|
| 21 | Площадь треугольника | 1 |
|
|
| 22 | Площадь трапеции | 1 |
|
|
| 23 | Решение задач на вычисление площадей фигур | 1 |
|
|
| 24 | Решение задач на нахождение площади | 1 |
|
|
| 25 | §3. Теорема Пифагора | 1 |
|
| Доказывать и применять теорему Пифагора при решении задач, а так же обратную ей теорему. Закрепить навыки решения задач по теме «Площадь». Проконтролировать знания уч-ся |
| 26 | Теорема, обратная теореме Пифагора | 1 |
|
|
| 27 | Решение задач по теме «Теорема Пифагора» | 1 |
|
|
| 28 | Решение задач | 1 |
|
|
| 29 | Решение задач | 1 |
|
|
| 30 | Контрольная работа №2 по теме «Площадь» | 1 |
|
|
| 31 | §1. Определение подобных треугольников. | 1 |
|
| Пропорциональные отрезки, св-ва пропорций, коэффициент подобия, теорема об отношении площадей подобных  , решения задач, используя определения подобных , решения задач, используя определения подобных  |
| 32 | Отношение площадей подобных треугольников | 1 |
|
|
| 33 | §2. Первый признак подобия треугольников | 1 |
|
| 1,2,3 признаки подобия  и их применение при решении задач и их применение при решении задач |
| 34 | Решение задач на применение первого признака подобия треугольников | 1 |
|
|
| 35 | Второй и третий признаки подобия треугольников | 1 |
|
|
| 36 | Решение задач на применение признаков подобия треугольников | 1 |
|
|
| 37 | Решение задач на применение признаков подобия треугольников | 1 |
|
|
| 38 | Контрольная работа №3 по теме «Признаки подобия треугольников» | 1 |
|
|
| 39 | §3. Средняя линия треугольника | 1 |
|
| Теорема о средней линии 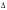 , св-во медиан , св-во медиан 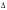 , применение при решении задач, теорема о подобии прямоугольных , применение при решении задач, теорема о подобии прямоугольных 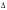 и следствия из неё, св-ва высоты прямоугольного и следствия из неё, св-ва высоты прямоугольного 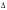 , задачи на построение, используя метод подобия , задачи на построение, используя метод подобия |
| 40 | Средняя линия треугольника. Свойство медиан треугольника. | 1 |
|
|
| 41 | Пропорциональные отрезки. | 1 |
|
|
| 42 | Пропорциональные отрезки в прямоугольном треугольнике. | 1 |
|
|
| 43 | Измерительные работы на местности | 1 |
|
|
| 44 | Задачи на построение методом подобия | 1 |
|
|
| 45 | Решение задач на построение методом подобных треугольников. | 1 |
|
|
| 46 | §4. Синус, косинус и тангенс острого угла прямоугольного треугольника | 1 |
|
| Основное тригонометрическое тождество, пользоваться таблицами Брадиса для определения значений синуса, косинуса, тангенса Применение основного тригонометрического тождества при решении задач |
| 47 | Значения синуса, косинуса и тангенса для углов 30˚, 45˚, 60˚. | 1 |
|
|
| 48 | Соотношения между сторонами и углами прямоугольного треугольника. Решение задач. | 1 |
|
|
| 49 | Контрольная работа №4. | 1 |
|
|
| 50 | §1. взаимное расположение прямой и окружности | 1 |
|
| Определение касательной, св-во и признак касательной, св-во отрезков касательной, проведенных их одной точки; уметь их доказывать |
| 51 | Касательная к окружности | 1 |
|
|
| 52 | Касательная к окружности. Решение задач. | 1 |
|
|
| 53 | §2. Градусная мера дуги окружности | 1 |
|
| Понятие дуги, полуокружности, центрального угла, градусной меры дуги окружности |
| 54 | Теорема о вписанном угле | 1 |
|
|
| 55 | Теорема об отрезках пересекающихся хорд | 1 |
|
|
| 56 | Решение задач по теме «Центральные и вписанные углы» | 1 |
|
|
| 57 | §3. Свойство биссектрисы угла | 1 |
|
| Док-во теорем и следствий из них, применять знания при решении задач |
| 58 | Серединный перпендикуляр | 1 |
|
|
| 59 | Теорема о точке пересечения высот треугольника | 1 |
|
|
| 60 | §4. Вписанная окружность | 1 |
|
| Док-во теоремы об окружности, вписанную в  , св-ва вписанного четырехуг., теоремы об окружности, описанной около , св-ва вписанного четырехуг., теоремы об окружности, описанной около  . Применять теоремы при решении задач . Применять теоремы при решении задач Умение применять свои знания при решении задач |
| 61 | Свойство описанного четырехугольника | 1 |
|
|
| 62 | Описанная окружность | 1 |
|
|
| 63 | Свойство вписанного четырехугольника | 1 |
|
|
| 64 | Решение задач по теме «Окружность» | 1 |
|
|
| 65 | Решение задач | 1 |
|
|
| 66 | Контрольная работа №5 по теме «Окружность» | 1 |
|
|
| 67 | Повторение по темам «Четырехугольники», «Площадь» | 1 |
|
|
|
| 68 | Повторение по теме «Подобные треугольники» | 1 |
|
|
|
| 69 | Повторение по теме «Окружность» | 1 |
|
|
|
| 70 | Резерв | 1 |
|
|
|
Отличительные особенности рабочей программы по сравнению с примерной программой.
Согласно учебного плана МБОУ Летошницкая СОШ на предмет «математика» отведено 175 часов.
Курс математики 8 класса состоит из курса алгебры и геометрии. Согласно программе: Макарычев Ю.Н., Алгебра 7 – 9 классы на изучение алгебры в 8-м классе отводится 102 часа.
Согласно программе: Атанасян Л.С. Геометрия 7-9 классы, на изучение геометрии отводится 68 часов.
Итого: 170 часов.
Пять часов резервное время, которое распределено следующим образом:
- на итоговое повторение изученного в 9 классе по алгебре -3 часа;
- на итоговое повторение изученного в 9-м классе по геометрии - 2 часа.
Всего: 170 + 5 = 175 часов








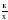 и её график.
и её график.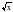 , её свойства и график.
, её свойства и график.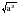 =
=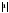 , которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида
, которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе дроби в выражениях вида 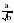 ,
, 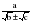 . Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа.
. Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа. 0, с использованием формулы корней. В данной теме учащиеся знакомятся с формулами Виета, выражающими связь между корнями квадратного уравнения и его коэффициентами. Они используются в дальнейшем при доказательстве теоремы о разложении квадратного трехчлена на линейные множители.
0, с использованием формулы корней. В данной теме учащиеся знакомятся с формулами Виета, выражающими связь между корнями квадратного уравнения и его коэффициентами. Они используются в дальнейшем при доказательстве теоремы о разложении квадратного трехчлена на линейные множители.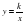 и ее график
и ее график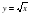 и её график
и её график и трапеции.
и трапеции. и их применение при решении задач
и их применение при решении задач









