ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ГОРОДА СЕВАСТОПОЛЯ
«СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №19 С УГЛУБЛЁННЫМ ИЗУЧЕНИЕМ АНГЛИЙСКОГО ЯЗЫКА»
| РАССМОТРЕНО на заседании МО учителей математики, ИКТ и черчения Протокол № 1 от «____» _______2016г.
| СОГЛАСОВАНО Заместитель директора по УВР ____________ Л.Г. Блажко
«29» августа 2016г.
| УТВЕРЖДАЮ директор ГБОУ СОШ №19 ___________ О.В. Настенко
Приказ от 01.09.2016г. №182
|
Рабочая программа
Наименование учебного предмета : алгебра
Класс : 8
Уровень общего образования : основное общее образование
Уровень изучения предмета: базовый
Срок реализации программы: 2016/2017
Предметная линия учебников: УМК по алгебре 7-9 класс (авторы Ю.М. Колягин, М.В. Ткачева, Н.Е. Федорова, М.И. Шабунин,
Учебник: Колягин Ю.М. Алгебра, 8 класс: учебник для общеобразовательных учреждений / Ю.М. Колягин, М.В. Ткачёва, Н.Е. Фёдорова, М.И. Шабунин. – М.: Просвещение, 2016
Год составления рабочей программы: 2016
ФИО учителя: Царева И.Ю.
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ГОРОДА СЕВАСТОПОЛЯ
«СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №19 С УГЛУБЛЁННЫМ ИЗУЧЕНИЕМ АНГЛИЙСКОГО ЯЗЫКА»
|
|
| УТВЕРЖДАЮ
директор ГБОУ СОШ №19 ___________ О.В.Настенко
Приказ от 01.09.2016г №182
|
Календарно-тематическое планирование
по алгебре 8 класс
на 2016-2017 учебный год
учитель : Царева И.Ю.
Пояснительная записка
Настоящая программа по алгебре для 8 класса (общеобразовательный уровень) составлена на основе Федерального компонента государственного стандарта среднего образования (приказ МОиН РФ от 05.03.2004г. № 1089), примерных программ по математике (письмо Департамента государственной политики в образовании Минобрнауки России от 07.07.2005г. № 03-1263), «Временных требований к минимуму содержания основного общего образования» (приказ МО РФ от 19.05.98. № 1236), примерной программы общеобразовательных учреждений по алгебре 7–9 классы к учебному комплексу для 7-9 классов (авторы Ю.М. Колягин, М.В. Ткачева, Н.Е. Федорова, М.И. Шабунин, составитель Т.А. Бурмистрова – М: Просвещение, 2011. – с. 21-27) .
Рабочая программа составлена с учетом следующего учебно - методического комплекта:
1. Колягин Ю.М. Алгебра, 8 класс: учебник для общеобразовательных учреждений / Ю.М. Колягин, М.В. Ткачёва, Н.Е. Фёдорова, М.И. Шабунин. – М.: Просвещение, 2012.
2. Ткачева М.В. Алгебра. Дидактические материалы, 8 класс. / М.В. Ткачева,
Н.Е. Фёдорова, М.И. Шабунин. – М.: Просвещение, 2011.
3. Колягин Ю.М. Изучение алгебры в 7-9 классах: Книга для учителя /
Ю.М. Колягин, Ю.В. Сидоров, М.В. Ткачева и др. – М.: Просвещение, 2002.
4. Лысенко Ф.Ф. Алгебра 7-8 . Тематические тесты и итоговые
работы. Легион. Ростов-на-Дону . 2013
5. Дидактические материалы. Алгебра. , 8 класс / А.Г.Мерзляк ,
В.Б.Полонский.М.Вентана-граф., 2015
Цели изучения математики:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование умений точно, грамотно, аргументировано излагать мысли как в устной, так и в письменной форме, овладение методами поиска, систематизации, анализа, классификации информации из различных источников (включая учебную, справочную литературу, современные информационные технологии);
формирование представлений об идеях и методах математики как средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Целью изучения алгебры является сознательное овладение учащимися системой алгебраических знаний и умений необходимо в повседневной жизни для изучения смежных дисциплин и продолжения образования.
Задачей школьного курса алгебры является развитие логического мышления учащихся. Сами объекты математических умозаключений и принятые в алгебре правила их конструирования способствуют формированию умений обосновывать и доказывать суждения, приводить чёткие определения, развивают логическую интуицию, кратко и наглядно раскрывают механизм логических построений и учат их применению.
Общая характеристика предмета :
алгебра занимает одно из ведущих мест в формировании научно-теоретического мышления школьников. Раскрывая внутреннюю гармонию математики, формируя понимание красоты и изящества математических рассуждений, алгебра вносит значительный вклад в эстетическое воспитание учащихся.
Практическая значимость школьного курса алгебры обусловлена тем, что её объектом являются количественные отношения действительного мира. Математическая подготовка необходима для понимания принципов устройства и использования современной техники, восприятия научных и технических понятий и идей. Математика является языком науки и техники. С её помощью моделируются и изучаются явления и процессы, происходящие в природе.
Алгебра является одним из опорных предметов основной школы: она обеспечивает изучение других дисциплин. В первую очередь это относится к предметам естественно-научного цикла, в частности, к физике. Развитие логического мышления учащихся при обучении алгебре способствует усвоению предметов гуманитарного цикла. Практические умения и навыки алгебраического характера необходимы для трудовой и профессиональной подготовки школьников.
Развитие у учащихся правильных представлений о сущности и происхождении алгебраических абстракций, соотношении реального и идеального, характере отражения математической наукой явлений и процессов реального мира, месте алгебры в системе наук и роли математического моделирования в научном познании и в практике способствует формированию научного мировоззрения учащихся и качеств мышления, необходимых для адаптации в современном информационном обществе.
Требуя от учащихся умственных и волевых усилий, концентрации внимания, активности развитого воображения, алгебра развивает нравственные черты личности (настойчивость, целеустремленность, творческую активность, самостоятельность, ответственность, трудолюбие, дисциплину и критичность мышления) и умение аргументированно отстаивать свои взгляды и убеждения, а также способность принимать самостоятельные решения.
Количество часов в неделю: 3 часа. Годовое количество часов: 102
Планируемые результаты :
Программа обеспечивает достижение следующих результатов освоения образовательной программы основного общего образования:
личностные:
сформированность ответственного отношения к учению, готовность и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессий и профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учётом устойчивых познавательных интересов;
сформированность целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики;
сформированность коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими, в образовательной, общественно полезной, учебно-исследовательской, творческой и других видах деятельности;
умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
представление о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;
критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
креативность мышления, инициатива, находчивость, активность при решении алгебраических задач;
умение контролировать процесс и результат учебной математической деятельности;
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
метапредметные:
умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
умение осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы;
умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
осознанное владение логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев, установления родовидовых связей;
умение устанавливать причинно-следственные связи; строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и выводы;
умение создавать, применять и преобразовывать знаковосимволические средства, модели и схемы для решения учебных и познавательных задач;
умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределение функций и ролей участников, взаимодействие и общие способы работы; умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;
сформированность учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.
предметные:
умение работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический), обосновывать суждения, проводить классификацию, доказывать математические утверждения;
владение базовым понятийным аппаратом: иметь представление о числе, владение символьным языком алгебры, знание элементарных функциональных зависимостей, формирование представлений о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
умение выполнять алгебраические преобразования рациональных выражений, применять их для решения учебных математических задач и задач, возникающих в смежных учебных предметах;
умение пользоваться математическими формулами и самостоятельно составлять формулы зависимостей между величинами на основе обобщения частных случаев и эксперимента;
умение решать линейные и квадратные уравнения и неравенства, а также приводимые к ним уравнения, неравенства, системы; применять графические представления для решения и исследования уравнений, неравенств, систем; применять полученные умения для решения задач из математики, смежных предметов, практики;
овладение системой функциональных понятий, функциональным языком и символикой, умение строить графики функций, описывать их свойства, использовать функционально-графические представления для описания и анализа математических задач и реальных зависимостей;
овладение основными способами представления и анализа статистических данных; умение решать задачи на нахождение частоты и вероятности случайных событий;
умение применять изученные понятия, результаты и методы при решении задач из различных разделов курса, в том числе задач, не сводящихся к непосредственному применению известных алгоритмов.
Содержание курса
Рациональные числа. Расширение множества натуральных чисел до множества целых. Множества целых чисел до множества рациональных. Рациональное число как отношение 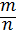
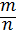 , где m — целое число, n — натуральное. Степень с целым показателем.
, где m — целое число, n — натуральное. Степень с целым показателем.
Действительные числа. Квадратный корень из числа.
Понятие об иррациональном числе. Иррациональность числа и несоизмеримость стороны и диагонали квадрата. Десятичные приближения иррациональных чисел.
Множество действительных чисел; представление действительных чисел бесконечными десятичными дробями. Сравнение действительных чисел.
Координатная прямая. Изображение чисел точками координатной прямой. Числовые промежутки.
Измерения, приближения, оценки. Размеры объектов окружающего мира (от элементарных частиц до Вселенной), длительность процессов в окружающем мире. Выделение множителя — степени десяти в записи числа. Приближённое значение величины, точность приближения. Прикидка и оценка результатов вычислений.
Алгебра
Алгебраические выражения. Буквенные выражения (выражения с переменными). Числовое значение буквенного выражения. Допустимые значения переменных. Подстановка выражений вместо переменных. Преобразование буквенных выражений на основе свойств арифметических действий. Равенство буквенных выражений. Тождество.
Алгебраическая дробь. Основное свойство алгебраической дроби. Сложение, вычитание, умножение, деление алгебраических дробей. Степень с целым показателем и её свойства.
Квадратные корни. Свойства арифметических квадратных корней и их применение к преобразованию числовых выражений и вычислениям.
Уравнения. Квадратное уравнение: формула корней квадратного уравнения. Теорема Виета. Решение уравнений, сводящихся к квадратным. Примеры решения уравнений третьей и четвёртой степеней. Решение дробно-рациональных уравнений.
Решение текстовых задач алгебраическим способом.
Декартовы координаты на плоскости. Графическая интерпретация уравнения с двумя переменными. Графики простейших нелинейных уравнений: парабола, гипербола, окружность. Графическая интерпретация систем уравнений с двумя переменными.
Неравенства. Числовые неравенства и их свойства.
Неравенство с одной переменной. Равносильность неравенств. Линейные неравенства с одной переменной. Квадратные неравенства. Системы неравенств с одной переменной.
Функции
Основные понятия. Зависимости между величинами. Понятие функции. Область определения и множество значений функции. Способы задания функции. График функции. Свойства функций, их отображение на графике. Примеры графиков зависимостей, отражающих реальные процессы.
Числовые функции. Функции, описывающие прямую и обратную пропорциональные зависимости, их графики и свойства. Линейная функция, её график и свойства. Квадратичная функция, её график и свойства.
Математика в историческом развитии
История формирования понятия числа: натуральные числа, дроби, недостаточность рациональных чисел для геометрических измерений, иррациональные числа. Старинные системы записи чисел. Дроби в Вавилоне, Египте, Риме. Открытие десятичных дробей. Старинные системы мер. Десятичные дроби и метрическая система мер. Появление отрицательных чисел и нуля. Л. Магницкий. Л. Эйлер.
Зарождение алгебры в недрах арифметики. Ал-Хорезми. Рождение буквенной символики. П. Ферма, Ф. Виет, Р. Декарт. История вопроса о нахождении формул корней алгебраических уравнений, неразрешимость в радикалах уравнений степени, большей четырёх. Н. Тарталья, Дж. Кардано, Н. X. Абель, Э. Галуа.
Изобретение метода координат, позволяющего переводить геометрические объекты на язык алгебры. Р. Декарт и П. Ферма. Примеры различных систем координат на плоскости.
Задача Леонардо Пизанского (Фибоначчи) о кроликах, числа Фибоначчи. Задача о шахматной доске.
Истоки теории вероятностей: страховое дело, азартные игры. П. Ферма и Б. Паскаль. Я. Бернулли. А. Н. Колмогоров.
Тематическое планирование
Содержание учебного предмета.
| № | ТЕМА | КОЛИЧЕСТВО ЧАСОВ | КОЛИЧЕСТВО КОНТРОЛЬНЫХ РАБОТ |
| 1 | Неравенства | 24 | 1 |
| 2 | Приближенные вычисления | 12 | 1 |
| 3 | Квадратные корни | 12 | 1 |
| 4 | Квадратные уравнения | 22 | 1 |
| 5 | Квадратичная функция | 15 | 1 |
| 6 | Квадратные неравенства | 12 | 1 |
| 7 | Повторение | 5 | 1 |
|
| Всего | 102 | 7 |
Неравенства. Положительные и отрицательные числа. Числовые неравенства, их свойства. Сложение и умножение неравенств. Строгие и нестрогие неравенства. Неравенства с одним неизвестным. Системы неравенств с одним неизвестным. Числовые промежутки.
Основная цель: сформировать у учащихся умение решать неравенства первой степени с одним неизвестным и их системы.
Приближенные вычисления. Приближенные значения величин. Погрешность приближения. Оценка погрешности. Округление чисел. Относительная погрешность. Простейшие вычисления на калькуляторе. Стандартный вид числа. Вычисление на калькуляторе степени и числа, обратного данному. Последовательное выполнение нескольких операций на калькуляторе. Вычисления на калькуляторе с использованием ячеек памяти.
Основная цель: познакомить учащихся с понятием погрешности приближения как показателем точности и качества приближения, выработать умение производить вычисления с помощью калькулятора.
Квадратные корни. Понятие арифметического квадратного корня. Действительные числа. Квадратный корень из степени, произведения и дроби.
Основная цель: систематизировать сведения о рациональных числах, ввести понятие иррационального и действительного числа, научить выполнять простейшие преобразования выражений, содержащих квадратные корни.
Квадратные уравнения. Квадратное уравнение и его корни. Неполные квадратные уравнения. Метод выделения полного квадрата. Решение квадратных уравнений. Разложение квадратного трехчлена на множители. Уравнения, сводящиеся к квадратным. Решение задач с помощью квадратных уравнений. Решение простейших систем, содержащих уравнения второй степени.
Основная цель: выработать умения решать квадратные уравнения, уравнения, сводящиеся к квадратным, и применять их к решению задач.
Квадратичная функция. Определение квадратичной функции. Функция у = х2, у = aх2, у = aх2+ bх+c. Построение графика квадратичной функции.
Основная цель: научить строить график квадратичной функции.
Квадратные неравенства. Квадратное неравенство и его решение. Решение квадратного неравенства с помощью графика квадратичной функции.
Основная цель: выработать умение решать квадратные неравенства с помощью графика квадратичной функции и метода интервалов.
Литература
Федеральный государственный образовательный стандарт общего образования.
Примерные программы основного общего образования. Математика. (Стандарты второго поколения). – М.: Просвещение, 2010.
Асмолов А.Г. Формирование универсальных учебных действий в основной школе. Система заданий / А.Г. Асмолов, О.А. Карабанова. – М.: Просвещение, 2010.
Колягин Ю.М. Алгебра, 8 кл.: учебник для общеобразовательных учреждений / Ю.М. Колягин, М.В. Ткачева, Н.Е. Федорова, М.И. Шабунин. – М.: Просвещение, 2012.
Ткачева М.В. Алгебра. Дидактические материалы, 8 класс. / М.В. Ткачева, Н.Е. Фёдорова, М.И. Шабунин. – М.: Просвещение, 2011.
Колягин Ю.М. Изучение алгебры в 7-9 классах: Книга для учителя / Ю.М. Колягин, Ю.В. Сидоров, М.В. Ткачева и др. – М.: Просвещение, 2002.
Алгебра. Тесты для промежуточной аттестации. 7-8 класс. / под ред. Ф.Ф. Лысенко - Ростов-на-Дону: Легион 2007.
Виртуальная школа Кирилла и Мефодия. Уроки алгебры Кирилла и Мефодия. 7-8 классы, 2004.
Глазков Ю.А. Алгебра. 8 класс. Тесты / Ю.А. Глазков, М.Я. Гаиашвили. – М.: Экзамен, 2011.
Дудницын Ю. П. Алгебра. Тематические тесты. 8 класс / Ю.П. Дудницын, В.Л. Кронгауз. – М.: Просвещение, 2010.
Жохов В.И. Алгебра. Дидактические материалы. 8 класс / В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк. – М.: Просвещение, 2010.
Жохов В.И. Уроки алгебры в 8 классе / В. И. Жохов, Г.Д. Карташева. – М.: Просвещение, 2010.
Живая математика. Учебно-методический комплект. Версия 4.3. Программа. Компьютерные альбомы. М: ИНТ.
Живая математика: Сборник методических материалов. М: ИНТ.
Макарычев Ю.Н. Изучение алгебры. 7-9 классы: книга для учителя / Ю.Н. Макарычев, Н.Г. Миндюк, С.Б. Суворова, И.С. Шлыкова. – М.: Просвещение, 2009.
КАЛЕНДАРНО-ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ
Алгебра 8 в класс . учитель Царева И.Ю.
2016/2017 учебный год
| № урока | Наименование раздела
и темы урока | Кол-во часов | Дата
| Дата проведения |
|
| Тема1: Неравенства | 24 ч |
|
|
| 1 | Повторение темы: «Одночлены и многочлены» | 1 |
|
|
| 2 | Повторение темы : «Разложение многочленов на множители» | 1 |
|
|
| 3 | Повторение темы: «Алгебраические дроби» | 1 |
|
|
| 4 | Положительные и отрицательные числа | 1 |
|
|
| 5 | Положительные и отрицательные числа | 1 |
|
|
| 6 | Числовые неравенства. Входной контроль | 1 |
|
|
| 7 | Основные свойства числовых неравенств | 1 |
|
|
| 8 | Основные свойства числовых неравенств | 1 |
|
|
| 9 | Сложение и умножение неравенств | 1 |
|
|
| 10 | Строгие и нестрогие неравенства | 1 |
|
|
| 11 | Неравенства с одним неизвестным | 1 |
|
|
| 12 | Решение неравенств | 1 |
|
|
| 13 | Решение неравенств | 1 |
|
|
| 14 | Решение неравенств | 1 |
|
|
| 15 | Системы неравенств с одним неизвестным. Числовые промежутки | 1 |
|
|
| 16 | Системы неравенств с одним неизвестным. Числовые промежутки | 1 |
|
|
| 17 | Решение систем неравенств | 1 |
|
|
| 18 | Решение систем неравенств | 1 |
|
|
| 19 | Решение систем неравенств | 1 |
|
|
| 20 | Решение систем неравенств | 1 |
|
|
| 21 | Модуль числа. Уравнения и неравенства, содержащие модуль | 1 |
|
|
| 22 | Модуль числа. Уравнения и неравенства, содержащие модуль | 1 |
|
|
| 23 | Обобщающий урок | 1 |
|
|
| 24 | Контрольная работа № 1 по теме «Неравенства» | 1 |
|
|
|
| Тема 2 : «Приближенные вычисления» | 12часов |
|
|
| 25/1 | Приближенные значения величин. Погрешность приближения | 1 |
|
|
| 26/2 | Оценка погрешности | 1 |
|
|
| 27/3 | Округление чисел | 1 |
|
|
| 28/4 | Относительная погрешность | 1 |
|
|
| 29/5 | Практические приемы приближенных вычислений | 1 |
|
|
| 30/6 | Практические приемы приближенных вычислений | 1 |
|
|
| 31/7 | Простейшие вычисления на микрокалькуляторе | 1 |
|
|
| 32/8 | Действия над числами, записанными в стандартном виде | 1 |
|
|
| 33/9 | Действия над числами, записанными в стандартном виде | 1 |
|
|
| 34/10 | Вычисление на микрокалькуляторе степени числа, обратного данному | 1 |
|
|
| 35/11 | Последовательное выполнение операций на микрокалькуляторе | 1 |
|
|
| 36/12 | Контрольная работа № 3 по теме «Приближенные вычисления» | 1 |
|
|
|
| Тема 3 : «Квадратные корни» | 12 часов |
|
|
| 37/1 | Арифметический квадратный корень | 1 |
|
|
| 38/2 | Арифметический квадратный корень | 1 |
|
|
| 39/3 | Действительные числа | 1 |
|
|
| 40/4 | Квадратный корень из степени | 1 |
|
|
| 41/5 | Квадратный корень из степени | 1 |
|
|
| 42/6 | Квадратный корень из произведения | 1 |
|
|
| 43/7 | Квадратный корень из произведения | 1 |
|
|
| 44/8 | Квадратный корень из дроби | 1 |
|
|
| 45/9 | Квадратный корень из дроби | 1 |
|
|
| 46/10 | Решение упражнений | 1 |
|
|
| 47/11 | Обобщающий урок | 1 |
|
|
| 48/12 | Контрольная работа № 3 по теме «Квадратные корни» | 1 |
|
|
|
| Тема 4 : «Квадратные уравнения» | 22часа |
|
|
| 49/1 | Квадратное уравнение и его корни | 1 |
|
|
| 50/2 | Квадратное уравнение и его корни | 1 |
|
|
| 51/3 | Неполные квадратные уравнения | 1 |
|
|
| 52/4 | Метод выделения полного квадрата | 1 |
|
|
| 53/5 | Решение квадратных уравнений | 1 |
|
|
| 54/6 | Решение квадратных уравнений | 1 |
|
|
| 55/7 | Решение квадратных уравнений | 1 |
|
|
| 56/8 | Приведенное квадратное уравнение. Теорема Виета | 1 |
|
|
| 57/9 | Приведенное квадратное уравнение. Теорема Виета | 1 |
|
|
| 58/10 | Приведенное квадратное уравнение. Теорема Виета | 1 |
|
|
| 59/11 | Уравнения, сводящиеся к квадратным | 1 |
|
|
| 60/12 | Уравнения, сводящиеся к квадратным | 1 |
|
|
| 61/13 | Уравнения, сводящиеся к квадратным | 1 |
|
|
| 62/14 | Решение задач с помощью квадратных уравнений | 1 |
|
|
| 63/15 | Решение задач с помощью квадратных уравнений | 1 |
|
|
| 64/16 | Решение задач с помощью квадратных уравнений | 1 |
|
|
| 65/17 | Решение простейших систем, содержащих уравнения второй степени | 1 |
|
|
| 66/18 | Решение простейших систем, содержащих уравнения второй степени | 1 |
|
|
| 67/19 | Различные способы решения систем уравнений | 1 |
|
|
| 68/20 | Решение задач с помощью систем уравнений | 1 |
|
|
| 69/21 | Обобщающий урок | 1 |
|
|
| 70/22 | Контрольная работа № 4 по теме «Квадратные уравнения» | 1 |
|
|
|
| Тема 5 : «Квадратичная функция» | 15часов |
|
|
| 71/1 | Определение квадратичной функции | 1 |
|
|
| 72/2 | Функция 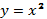 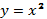 | 1 |
|
|
| 73/3 | Функция 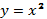 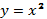 | 1 |
|
|
| 74/4 | Функция 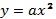 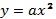 | 1 |
|
|
| 75/5 | Функция 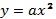 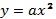 | 1 |
|
|
| 76/6 | Функция 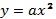 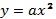 | 1 |
|
|
| 77/7 | Функция 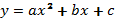 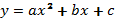 | 1 |
|
|
| 78/8 | Функция 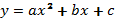 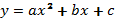 | 1 |
|
|
| 79/9 | Функция 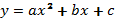 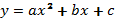 | 1 |
|
|
| 80/10 | Построение графика квадратичной функции | 1 |
|
|
| 81/11 | Построение графика квадратичной функции | 1 |
|
|
| 82/12 | Построение графика квадратичной функции | 1 |
|
|
| 83/13 | Построение графика квадратичной функции | 1 |
|
|
| 84/14 | Обобщающий урок | 1 |
|
|
| 85/15 | Контрольная работа № 5 по теме «Квадратичная функция» | 1 |
|
|
|
| Тема 6 : «Квадратные неравенства» | 12 часов |
|
|
| 86/1 | Работа над ошибками | 1 |
|
|
| 87/2 | Квадратное неравенство и его решение | 1 |
|
|
| 88/3 | Квадратное неравенство и его решение | 1 |
|
|
| 89/4 | Решение квадратного неравенства с помощью графика квадратичной функции | 1 |
|
|
| 90/5 | Решение квадратного неравенства с помощью графика квадратичной функции | 1 |
|
|
| 91/6 | Решение квадратного неравенства с помощью графика квадратичной функции | 1 |
|
|
| 92/7 | Решение квадратного неравенства с помощью графика квадратичной функции | 1 |
|
|
| 93/8 | Решение квадратного неравенства с помощью графика квадратичной функции | 1 |
|
|
| 94/9 | Метод интервалов | 1 |
|
|
| 95/10 | Метод интервалов | 1 |
|
|
| 96/11 | Обобщающий урок | 1 |
|
|
| 97/12 | Контрольная работа № 6 по теме «Квадратные неравенства» | 1 |
|
|
|
| Тема 7 : «Повторение» | 5 часов |
|
|
| 98/ | Повторение темы «Квадратные корни» | 1 |
|
|
| 99 | Повторение темы «Квадратные уравнения» | 1 |
|
|
| 100 | Повторение темы «Неравенства. Квадратные неравенства» | 1 |
|
|
| 101 | Итоговая контрольная работа № 7 | 1 |
|
|
| 102 | Итоговый урок | 1 |
|
|
Литература
Федеральный государственный образовательный стандарт общего образования.
Примерные программы основного общего образования. Математика. (Стандарты второго поколения). – М.: Просвещение, 2010.
Асмолов А.Г. Формирование универсальных учебных действий в основной школе. Система заданий / А.Г. Асмолов, О.А. Карабанова. – М.: Просвещение, 2010.
Колягин Ю.М. Алгебра, 8 кл.: учебник для общеобразовательных учреждений / Ю.М. Колягин, М.В. Ткачева, Н.Е. Федорова, М.И. Шабунин. – М.: Просвещение, 2012.
Ткачева М.В. Алгебра. Дидактические материалы, 8 класс. / М.В. Ткачева, Н.Е. Фёдорова, М.И. Шабунин. – М.: Просвещение, 2011.
Колягин Ю.М. Изучение алгебры в 7-9 классах: Книга для учителя / Ю.М. Колягин, Ю.В. Сидоров, М.В. Ткачева и др. – М.: Просвещение, 2002.
Алгебра. Тесты для промежуточной аттестации. 7-8 класс. / под ред. Ф.Ф. Лысенко - Ростов-на-Дону: Легион 2007.
Виртуальная школа Кирилла и Мефодия. Уроки алгебры Кирилла и Мефодия. 7-8 классы, 2004.
Глазков Ю.А. Алгебра. 8 класс. Тесты / Ю.А. Глазков, М.Я. Гаиашвили. – М.: Экзамен, 2011.
Дудницын Ю. П. Алгебра. Тематические тесты. 8 класс / Ю.П. Дудницын, В.Л. Кронгауз. – М.: Просвещение, 2010.
Жохов В.И. Алгебра. Дидактические материалы. 8 класс / В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк. – М.: Просвещение, 2010.
Жохов В.И. Уроки алгебры в 8 классе / В. И. Жохов, Г.Д. Карташева. – М.: Просвещение, 2010.
Живая математика. Учебно-методический комплект. Версия 4.3. Программа. Компьютерные альбомы. М: ИНТ.
Живая математика: Сборник методических материалов. М: ИНТ.
Макарычев Ю.Н. Изучение алгебры. 7-9 классы: книга для учителя / Ю.Н. Макарычев, Н.Г. Миндюк, С.Б. Суворова, И.С. Шлыкова. – М.: Просвещение, 2009.
ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ИЗУЧЕНИЯ КУРСА АЛГЕБРЫ
В 8 КЛАССЕ
РАЦИОНАЛЬНЫЕ ЧИСЛА
Ученик научится:
понимать особенности десятичной системы счисления;
владеть понятиями, связанными с делимостью натуральных чисел;
выражать числа в эквивалентных формах, выбирая наиболее подходящую в зависимости от конкретной ситуации;
сравнивать и упорядочивать рациональные числа;
выполнять вычисления с рациональными числами, сочетая устные и письменные приёмы вычислений, применение калькулятора;
использовать понятия и умения, связанные с пропорциональностью величин, процентами в ходе решения математических задач и задач из смежных предметов, выполнять несложные практические расчеты.
Ученик получит возможность:
познакомиться с позиционными системами счисления с основаниями, отличными от 10;
углубить и развить представления о натуральных числах и свойствах делимости;
научиться использовать приёмы, рационализирующие вычисления, приобрести привычку контролировать вычисления, выбирая подходящий для ситуации способ.
ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
Ученик научится:
использовать начальные представления о множестве действительных чисел;
владеть понятием квадратного корня, применять его в вычислениях.
Ученик получит возможность:
развить представление о числе и числовых системах от натуральных до действительных чисел; о роли вычислений в человеческой практике;
развить и углубить знания о десятичной записи действительных чисел (периодические и непериодические дроби).
ИЗМЕРЕНИЯ, ПРИБЛИЖЕНИЯ, ОЦЕНКИ
Ученик научится:
использовать в ходе решения задач элементарные представления, связанные с приближёнными значениями величин.
Ученик получит возможность:
понять, что числовые данные, которые используются для характеристики объектов окружающего мира, являются преимущественно приближёнными, что по записи приближённых значений, содержащихся в информационных источниках, можно судить о погрешности приближения;
понять, что погрешность результата вычислений должна быть соизмерима с погрешностью исходных данных.
АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ
Ученик научится:
владеть понятиями «тождество», «тождественное преобразование», решать задачи, содержащие буквенные данные; работать с формулами;
выполнять преобразования выражений, содержащих степени с целыми показателями и квадратные корни;
выполнять тождественные преобразования рациональных выражений на основе правил действий над многочленами и алгебраическими дробями;
выполнять разложение многочленов на множители.
Ученик получит возможность:
научиться выполнять многошаговые преобразования рациональных выражений, применяя широкий набор способов и приёмов;
применять тождественные преобразования для решения задач из различных разделов курса (например, для нахождения наибольшего/наименьшего значения выражения).
УРАВНЕНИЯ
Ученик научится:
решать основные виды квадратных уравнений;
понимать уравнение как важнейшую математическую модель для описания и изучения разнообразных реальных ситуаций, решать текстовые задачи алгебраическим методом;
применять графические представления для исследования уравнений.
Ученик получит возможность:
овладеть специальными приёмами решения уравнений и систем уравнений; уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики;
применять графические представления для исследования уравнений, систем уравнений, содержащих буквенные коэффициенты.
НЕРАВЕНСТВА
Ученик научится:
понимать и применять терминологию и символику, связанные с отношением неравенства, свойства числовых неравенств;
решать линейные неравенства с одной переменной и их системы; решать квадратные неравенства с опорой на графические представления;
применять аппарат неравенств для решения задач из различных разделов курса.
Ученик получит возможность научиться:
разнообразным приёмам доказательства неравенств; уверенно применять аппарат неравенств для решения разнообразных математических задач и задач из смежных предметов, практики;
применять графические представления для исследования неравенств, систем неравенств, содержащих буквенные коэффициенты.
ОСНОВНЫЕ ПОНЯТИЯ. ЧИСЛОВЫЕ ФУНКЦИИ
Ученик научится:
понимать и использовать функциональные понятия и язык (термины, символические обозначения);
строить графики элементарных функций; исследовать свойства числовых функций на основе изучения поведения их графиков;
понимать функцию как важнейшую математическую модель для описания процессов и явлений окружающего мира, применять функциональный язык для описания и исследования зависимостей между физическими величинами.
Ученик получит возможность научиться:
проводить исследования, связанные с изучением свойств функций, в том числе с использованием компьютера; на основе графиков изученных функций строить более сложные графики (кусочно-заданные, с «выколотыми» точками и т. п.);
использовать функциональные представления и свойства функций для решения математических задач из различных разделов курса.
Количество часов в неделю: 3
Годовое количество часов: 102
Планирование составлено на основе:
Программы для общеобразовательных учреждений: Алгебра для 7-9 классов, составитель Бурмистрова Т.А. – М.: Просвещение, 2011.
Колягин Ю.М. Алгебра, 8 класс: учебник для общеобразовательных учреждений / Ю.М. Колягин, М.В. Ткачёва, Н.Е. Фёдорова, М.И. Шабунин. – М.: Просвещение, 2012.
Дополнительная литература:
Ткачева М.В. Алгебра. Дидактические материалы, 8 класс. / М.В. Ткачева, Н.Е. Фёдорова, М.И. Шабунин. – М.: Просвещение, 2011.
Колягин Ю.М. Изучение алгебры в 7-9 классах: Книга для учителя / Ю.М. Колягин, Ю.В. Сидоров
21

















