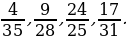У р о к № 1. Приведение дробей к общему знаменателю
Основная дидактическая цель урока: ввести понятие дополнительного множителя, отрабатывать умения приводить дроби к новому знаменателю и находить дополнительный множитель, закрепить знание основного свойства дроби и умение сокращать дроби, развивать математическую речь.
Х о д у р о к а
I. Организационный момент
II. Устная работа
– Какие из данных дробей можно представить со знаменателем 48?
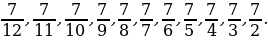
III. Работа по теме урока
1. С. 61–62 (работа по статье учебника).
– Приведите дробь 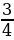 к знаменателю 8.
к знаменателю 8.
– К какому новому знаменателю можно привести данную дробь? (Дробь можно привести к любому знаменателю, кратному знаменателю данной дроби.)
Число, на которое надо умножить знаменатель дроби, чтобы получить новый знаменатель, называют дополнительным множителем.
– Прочитайте в учебнике на с. 61 о дроби 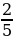 . На что умножают числитель и знаменатель дроби при приведении её к новому знаменателю? (На дополнительный множитель.)
. На что умножают числитель и знаменатель дроби при приведении её к новому знаменателю? (На дополнительный множитель.)
– Что нужно сначала найти, чтобы привести дроби к новому знаменателю? (Дополнительный множитель.)
– Изменилась ли дробь после её приведения к новому знаменателю? (Мы получили дробь, равную данной.)
Любые две дроби можно привести к одному и тому же знаменателю, или, иначе, к общему знаменателю. Например, 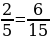 и
и 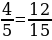 .
.
– Выучите правило приведения дроби к наименьшему общему знаменателю.
– Как привести дроби 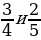 к общему знаменателю?
к общему знаменателю?
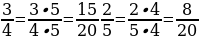
2. С. 62, № 5.365.
– Что интересного вы заметили? (Числитель новой дроби равен количеству минут.)
Ответ: 15 с, 25 с, 50 с, 36 с, 36 с, 20 с, 34 с, 39 с.
3. С. 62, № 5.366.
а) 4 : 2 = 2 → 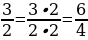
б) 10 : 5 = 2 → 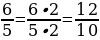
в) 12 : 6 = 2 → 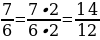
г) 100 : 5 = 20 → 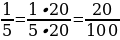
д) 30 : 5 = 6 → 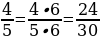
е) 1000 : 50 = 20 → 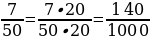
IV. Повторение изученного материала
1. С. 63, № 5.377 (устно). (На 2, 18, 8. 12, 4.)
2. С. 63, № 5.379 (работа в паре).
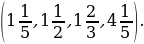
V. Работа над задачей
С. 64, № 5.382.
– Что известно? Что надо узнать?
– Что можно узнать? (Скорость сближения.)
– Как найти расстояние, зная скорость и время? (Скорость умножить на время.)
Решение:
1) 600 : 12 = 50 (м/мин) – скорость течения реки.
2) 200 + 50 = 250 (м/мин) – скорость лодки по течению.
3) 250 - 50 = 200 (м/мин) – скорость сближения.
4) 600 : 200 = 3 (мин) – лодка пройдёт 600 м.
5) 12 + 3 = 15 (мин) – встреча лодки и плота.
6) 15 ・ 50 = 750 (м) – от берега.
Ответ: 750 м от места стоянки лодка догонит плот.
VI. Работа в рабочей тетради
С. 17, № 1, 2.
VII. Рефлексия
– К какому новому знаменателю можно привести дробь 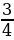 ?
?
– Можно ли привести дробь 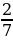 к знаменателю 35? к знаменателю 25?
к знаменателю 35? к знаменателю 25?
– Какое число называют дополнительным множителем?
– Как найти дополнительный множитель?
– Как привести дроби к наименьшему общему знаменателю?
– Объясните, почему несократимы дроби: 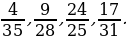
Домашнее задание
С. 64, № 5.387, 5.389.







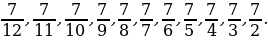
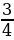 к знаменателю 8.
к знаменателю 8.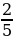 . На что умножают числитель и знаменатель дроби при приведении её к новому знаменателю? (На дополнительный множитель.)
. На что умножают числитель и знаменатель дроби при приведении её к новому знаменателю? (На дополнительный множитель.)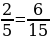 и
и 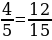 .
.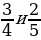 к общему знаменателю?
к общему знаменателю?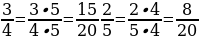
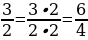
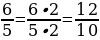
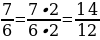
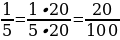
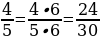
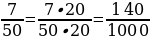
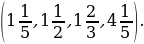
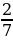 к знаменателю 35? к знаменателю 25?
к знаменателю 35? к знаменателю 25?