Алгебра (7) Дата : 19.11.2024
Урок № 31
Тема урока : Преобразование буквенных выражений, раскрытие скобок и приведение подобных слагаемых
Образовательная цель: рассмотреть действия с буквенными выражениями
Развивающая цель: развить познавательный интерес учащихся, наблюдательность, логику, память, внимание.
Воспитательная цель: точность аккуратность математической записи.
Тип урока. Урок усвоения новых знаний и умений.
Метод. Словесный, беседа, рассказ
Ключевые слова: числовые выражения, преобразование буквенных выражений и вычисления, составление уравнения
Литература / основная/
Ход урока
-
Организационный момент
*проверка посещаемости;
*проверка готовности к уроку;
Проверка д/з выборочно.
-
Актуализация опорных базовых знаний
-
Выполнить преобразование:
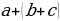 = a+b+c ;
= a+b+c ;
-
Выполнить преобразование:
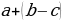 = a+b - c ;
= a+b - c ;
-
Выполнить преобразование:
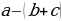 = a - b - c ;
= a - b - c ;
-
Выполнить преобразование:
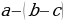 = a - b + c ;
= a - b + c ;
3.Мотивация учебной деятельности. Сообщение темы, цели , задачи урока. Если перед скобками стоит знак «+» мы просто убираем скобки. Если перед скобками стоит знак «-», то мы знаки в скобках меняем на противоположные.
Формирование умений навыков. ЗАДАНИЕ №1
Для преобразования буквенных выражений с помощью раскрытия скобок используют распределительное свойство умножения.
№1.
Выучи правило раскрытия скобок, если перед скобкой стоит знак «+» и запиши пример в тетрадь.
*Если перед скобкой стоит знак «+»,то при раскрытии скобок у алгебраических слагаемых сохраняются свои знаки.
а + (-b+ с- d)= а-b+с-d
1.Опустить знак «+» перед скобкой;
2. Опустить скобки: Чтобы раскрыть скобки, перед которыми стоит знак « +», нужно:
3.Каждое слагаемое, стоящее в скобках,записать со своим знаком.
Пример:
7+5(3а -7b+4с)= 7+15а-35b+20;
№2.Выучи правило раскрытия скобок, если перед скобкой стоит знак «-» и запиши пример в тетрадь.
3.Каждое слагаемое, стоящее в скобках, записать с противоположным знаком.
Пример:
4,6- (2а -3b +7с) = 4,6-2а+3b-7с;
№ 3. Раскрой скобки(реши четные или нечетные примеры)(8б.)
1) 8( х + у);
2) -2,1(а- b);
3) 4 (5- b);
4)-2(-4-2х);
5)3(2а+3у);
№4.Раскройте скобки
-
a +( b-c); 4) 9-( a+b+c); 7) a - (b - c+d);
-
x-(y+2); 5) x-(-3+y-z); 3) x+ (y-z+8); 5) m- (-2+n+k). Задание № 2
№1.Рассмотрим преобразование буквенного выражения вынесением общего множителя за скобки.
Поменяв местами правую и левую части равенства,выражающего распределительное свойство умножения, получим:
ас + bс = (а + b) с, где с- общий множитель
Переход от суммы ас + bс к произведению (а+ b) с – называют вынесением общего множителя за скобки.
Пример:
а) 2а +2b= 2 (а+b), где число 2- общий множитель;
б) -3а-3b = -3 (а+b), где число -3- общий множитель;
в)12х+15у-21z =3 (4x+5y-7z); где число 3- общий множитель.
№2.Вынесите общий множитель за скобки:
1) 4х – 2у; 2) ах –bх; 3) 2,5 а-3b;
15а + 21b; ху -2у; 0,6 х - 0,8 у;
35х – 20у; 5х +10у; 1,8 а + 2,7 b.
№3.Реши на выбор одну задачу
№1.Ученик купил 4 тетради и 4 альбома, цена тетради а тенге, а цена альбома b тенге. Сколько стоит вся покупка, если а =90, b=150?
№2. Длина прямоугольника 16 см, а ширина m см. Найдите периметр прямоугольника, если m=9.
Задание №3
Рассмотрим упрощение алгебраических выражении приведением подобных слагаемых.
№1. Слагаемые, имеющие одинаковую буквенную часть, называют подобными слагаемыми.
*Сложение подобных слагаемых называется произведением подобных слагаемых.
Чтобы привести подобные слагаемые, надо:
1.Сложить их коэффициенты;
2.Полученное число умножить на общую буквенную часть.
Алгебраическая сумма может содержать различные группы подобных слагаемых. В этом случае их следует подчеркнуть по разному.
Пример:
-
3х- 6х+7х = (3 – 8 + 7) х = 2х; х- общий множитель.
-
2,5х– 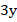 + 1,2z + 7x – 5z +1,8y = (2,5 +7) x + (-3+1,8) y + (1,2 -5)z =9,5x-1,2y -3,8z.
+ 1,2z + 7x – 5z +1,8y = (2,5 +7) x + (-3+1,8) y + (1,2 -5)z =9,5x-1,2y -3,8z.
№2. Приведите подобные слагаемые (Реши четные или нечетные примеры)
1) 2а – 8а + 3а; 3) 3 (а -1,7); 5) 0,6с – с + 0,5с;
2) 7а – 13а – 4а; 4) 8b+4b -7b; 6) 2,9с + 3с – 10с.
№3. Раскройте скобки и упростите:(реши на выбор 4 примера) (8б.)
1) 1,9 (а +2); 4) 3 (а – 1,7); 7) -2 (х - 0,9);
2) 0,3 – (а -2); 5) а- (2,7 +а); 8) 10- (8 -a);
-a);
3) а + b– (а –b); 6) 1 + (b– 2
+ (b– 2  ); 9) – 4 ( х +у).
); 9) – 4 ( х +у).
№4.Реши выборочно одну задачу
-
В книжном шкафу 3 полки. На первой полке а книг. На второй полке на 6 книг больше, чем на первой полке, а на третьей полке на 2 книги меньше,чем на второй. Сколько всего книг в книжном шкафу?
2.Путешественник проехала км на велосипеде, а на машине на 80 км больше. Сколько всего километров проехал путешественник?
Задание №5
№1. Упростите выражения, раскрывая скобки: (Реши на выбор 3 примера)
1) 3х (а +1,5) – 4ах; 3) -5(1,8-у)+7; 5) -6 (а –b) – 2(а -3b);
2) m (n –k) +mk;4) 2,3 ( b – 8) – (b-3,4);6)-6 (x +y) +3 (2x+y).
№2 Вынесите общий множитель за скобки:
1) аb +b –by ; 3) ax – bx –cy +dy ;
2) 3a – 6b +12c ; 4) 4a -12b -8c -32d.
№3Реши на выбор одну задачу.(4б.)
1.Рукопись содержит а страниц. В первый день оператор набрал на компьютере  всей рукописи, а во второй день -
всей рукописи, а во второй день -  всей рукописи. Сколько страниц осталось набрать оператору ?
всей рукописи. Сколько страниц осталось набрать оператору ?
2. Младшему брату х лет,возраст старшего брата больше в 1,5 раза, а возраст отца больше в 3,5 раза. Дедушке столько, сколько сыну и внукам, вместе взятым. Сколько лет дедушке ? Составьте выражение и получите его значение при х=12.
Задание №6
№ 1 Реши на выбор одно уравнение:
1) 0,3 – ( 7,1+х)= - 1,5; 3) 9,4 – (1,6 –у)=11,8 ;
2) х +11 – (2х-5 ; 4) 7(1,2х-5) +18 –х =5,2.
№ 2 Выпишите из данных выражении тождественно равные
1) -( а- bx - c) ; 3) 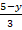 ; 5) 0,6 a
; 5) 0,6 a 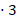 ; 7)1,8a ;
; 7)1,8a ;
2) 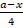 ; 4)
; 4) 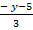 ; 6)
; 6)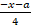 ;8) –a+bx+c.
;8) –a+bx+c.
№ 3 Упростите выражение и найдите его значение:
1) 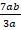 +
+  b при b=
b при b=  ; 2)
; 2) 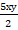 :
: 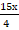 при у =0,25.
при у =0,25.
6.Подведение итогов урока. Анализ работы в классе. Оценивание.
7. Домашнее задание:







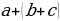 = a+b+c ;
= a+b+c ;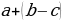 = a+b - c ;
= a+b - c ;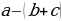 = a - b - c ;
= a - b - c ;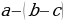 = a - b + c ;
= a - b + c ;


















