М(5) Дата: 27.11.2024
У р о к № 58 -59 Тема: « Дробь. Правильные и неправильные дроби»
Образовательная цель: организация деятельности учащихся на закрепления понятия обыкновенная дробь, правильная и неправильная дробь сравнительно с единицей, рассмотреть нахождение дроби от числа.
Развивающая цель: развитие логики, памяти , внимания.
Воспитательная цель: точность, аккуратность математической записи.
Планируемые результаты:
-личностные
1. Формирование устойчивого познавательного интереса
2. Развитие коммуникативной компетенции при общении и сотрудничестве
3. Формирование у учащихся ответственного отношения к учению, готовности и способности к саморазвитию на основе мотивации к обучению и познанию
- метапредметные результаты:
1. Освоение способности представлять результаты решения заданий на дроби
Тип урока. Урок сообщения новых знаний
Метод. Словесный, беседа, рассказ.
Литература /основная/ Н. Я, Виленкин и др. Математика 5 класс, часть 1
Дополнительная литература: ФГОС в помощь школьному учителю. Автор И. А, Чердаклиева . Поурочные разработки по математике к УМК Н. Я. Виленкин и др., 5 класс .
Обязательная литература:
Никольский С. М. Математика. 5 класс: Учебник для общеобразовательных учреждений. / ФГОС // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 272 с.
Ход урока
Организационный момент .
проверка посещаемости;
проверка готовности к уроку;
проверка дз
Актуализация знаний.
Устный счёт
числитель и знаменатель обыкновенной дроби;
правильная, неправильная дробь.
Мотивация учебной деятельности. Мы уже знаем, что дробь в математике – число, состоящее из одной или нескольких равных частей (долей) единицы.
Правильные дроби – это дроби, в которых числитель меньше знаменателя
Неправильные дроби – это дроби, в которых числитель равен или больше знаменателя. 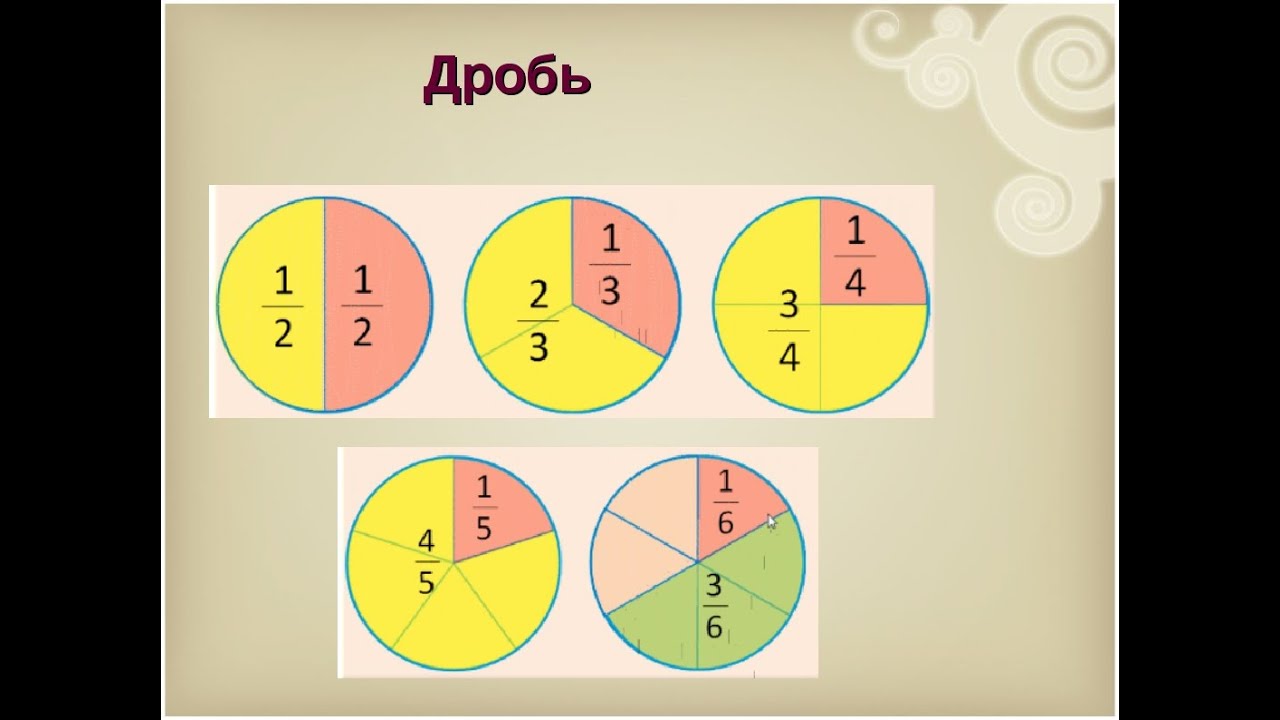
Сообщение нового материала.
Правильные и неправильные дроби
1. Слово «дробь» обозначало часть, то есть меньше целого, те дроби, которые обозначают количество, меньшее единицы, назвали - « правильными » дробями, а остальные – « неправильными ».
То есть дроби 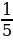 и
и 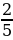 называются правильными, так как они меньше единицы.
называются правильными, так как они меньше единицы.

А вот уже 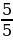 и
и 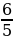 – неправильными.
– неправильными.

Если числитель меньше знаменателя, то дробь меньше единицы и мы называем ее правильной.
Если числитель равен знаменателю, то дробь равна единице и уже называется неправильной.
Если числитель больше знаменателя, то дробь больше единицы и тоже неправильная.
Пример
Правильные дроби со знаменателем 259:
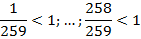
Неправильные дроби со знаменателем 259:
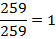
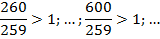
Сравним следующие дроби: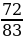 ,
, 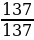 ,
,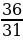
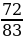 – правильная дробь, меньше единицы;
– правильная дробь, меньше единицы;
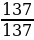 – неправильная, равна единице;
– неправильная, равна единице;
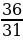 – неправильная , больше единицы.
– неправильная , больше единицы.
Таким образом: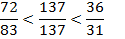
Нахождение дроби от числа.
Пример 1. Потренируемся находить дроби от разных количеств. В классе 30 человек.  класса пойдет на французский язык,
класса пойдет на французский язык,  класса – на английский. Сколько человек каким языком будет заниматься?
класса – на английский. Сколько человек каким языком будет заниматься?
Чтобы найти  от 30, нужно класс разделить на три равные части, то есть 30 разделить на 3. Тот факт, что мы ищем
от 30, нужно класс разделить на три равные части, то есть 30 разделить на 3. Тот факт, что мы ищем  от 30, будем записывать как
от 30, будем записывать как 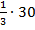 . Предлог «от» мы заменяем знаком умножения:
. Предлог «от» мы заменяем знаком умножения:
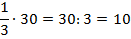
Полученное число 10 – это и есть доля  от общего количества учеников, от 30. Мы выяснили, что 10 учеников пойдут заниматься французским языком.
от общего количества учеников, от 30. Мы выяснили, что 10 учеников пойдут заниматься французским языком.
Найдем  общего количества учеников, то есть
общего количества учеников, то есть  от 30. Разделим 30 на 3 и умножим полученный результат на два.
от 30. Разделим 30 на 3 и умножим полученный результат на два.
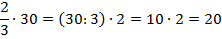
Найдем 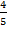 от общего количества учеников, то есть
от общего количества учеников, то есть 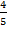 от 30 или
от 30 или 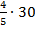 . Делим 30 на 5, получаем
. Делим 30 на 5, получаем 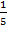 от 30, а именно 6. Тогда
от 30, а именно 6. Тогда 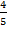 от 30 будет равна четырем таким долям, то есть 24.
от 30 будет равна четырем таким долям, то есть 24.
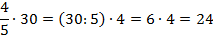
Закрепление:
1. Если дробь меньше единицы, то ее называют правильной. В этом случае числитель всегда меньше знаменателя.
2. Если у дроби числитель и знаменатель равны, то дробь равна единице и называется неправильной.
3. Если числитель больше знаменателя, то дробь больше единицы и тоже называется неправильной.
Подведение итогов урока.
Рефлексия. Домашнее задание:








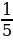 и
и 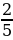 называются правильными, так как они меньше единицы.
называются правильными, так как они меньше единицы.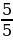 и
и 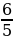 – неправильными.
– неправильными.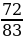 ,
, 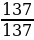 ,
,