Россия, Челябинск
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 21.05.2022 22:09
Люнченко Вера Дмитриевна
учитель математики
67 лет
1 330
46 623 
Местоположение
Специализация
Разработка урока математики в 8 классе. Тема "Функции и их графики"
Категория:
Математика
08.11.2016 22:09
Просмотр содержимого документа
«Разработка урока математики в 8 классе. Тема "Функции и их графики"»
Конспект урока алгебры в 8 классе
Учитель: Люнченко Вера Дмитриевна, учитель математики высшей категории, МБОУ «С(К)ОШ №11 г. Челябинска»
Тема: «Функции и хи графики ».
Цели урока:
Образовательная:
1. Повторение ранее изученного материала по теме.
2. Осознание учащимися усвоения темы функции обратной пропорциональности.
3. Подготовка к изучению темы: «Функция y = √ х, ее свойства и график» .
Развивающая:
Способствовать:1.Развитию мыслительной деятельности на уроке, тренировке памяти.
Воспитательная:
Содействие воспитанию: 1. Самореализации в процессе подготовки и проведения урока.
2. Адекватного контроля и самооценивания своего труда.
Оборудование: магнитная доска, плакат с кроссвордом; карточки с заданиями, индивидуальная ведомость ученика, автоматизированное рабочее место (АРМ ) учителя, проектор.
Структура урока:
1. Организационный этап.
2. Этап проверки домашнего задания.
3. Историческая справка
4. Этап подготовки учащихся к активному усвоению знаний.
5. Этап повторения.
6. Этап проверки знаний.
7. Этап информации о домашнем задании.
8. Рефлексия. Итоги урока.
Примерная продолжительность этапов урока
| № этапа | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Время (мин.) | 3 | 6 | 5 | 7 | 10 | 10 | 2 | 2 |
Ход урока:
| № этапа урока | Название этапа. Основное содержание учебного материала | Деятельность учителя | Деятельность учащихся |
| 1 | Организационный этап. | Приветствует учеников, интересуется их настроением, объявляет тему и цели урока.
| Приветствуют учителя, мысленно осознают задачи, которые необходимо усвоить на уроке. |
| 2 | Этап проверки домашнего задания. Домашнее задание проверяется в два этапа: на первом учитель просит ребят самим оценить свою работу. На втором этапе ученики обмениваются тетрадями и проверяют работу соседа по образцу решения домашнего задания на экране..
| 1. Консультирует и следит за самоконтролем учащихся.
2.Выводит решение домашнего задания на экран .
3. Консультирует и следит за процессом оценивания заданий. 4.«Спорные » работы учитель сам проверяет после урока | 1. ученики проверяют свое домашнее задание и ставят сами себе отметку на полях синей пастой, обводят в круг. 2.Обмениваются тетрадями с соседом. 3. Проверяют задание соседа и под ним ставят отметку. 4.Отметки тех работ, в которых они совпали, ученики выставляют в индивидуальную ведомость ученика. |
| 3 | Историческая справка.
Сообщение проходит под спокойную мелодию, участвуют в нем 4-5 учащихся, которые выступают коротко, сидя на своих рабочих местах. | Включает мелодию. Вместе с учениками слушает сообщения. | Ученики сообщают заранее подготовленную краткую историческую справку об открытии известных функций и интересных фактах о них. |
| 4 | Этап подготовки учащихся к активному усвоению знаний. Учащимся предлагается разгадать кроссворд, который заранее подготовлен на большом листе бумаги. | Зачитывает вопросы к кроссворду. [Приложение 1] В процессе ответов за правильные полные ответы учитель выдает красные прямоугольники, за неполные и неточные ответы – зеленые полукруги. Каждый прямоугольник оценивается в 1 балл, каждый полукруг оценивается в 0,5 балла.
| 1. Один из учеников записывает правильные ответы в кроссворд. 2 После решения кроссворда, ученики подсчитывают набранные баллы и записывают их в индивидуальную ведомость ученика. |
| 5 | Этап повторения. Пока вызванные к доске ученики работают, весь класс отвечает на вопросы, которые появляются на экране [Приложение 4] После фронтального разбора вопросов внимание класса привлекается к ученикам, работающим у доски. После этого к доске приглашается новая тройка учеников для выполнения на доске нового задания: «По данным в таблице координатам (х; у) построить на координатной плоскости соответствующие точки.»
| 1.Учитель задает классу вопрос: «Какие основные способы задания функции Вы знаете?» и после ответа вызывает3 учеников к доске для работы по карточкам. 2. Контролирует правильность ответов учеников при фронтальной работе. 3 Разбирает вместе с ребятами таблицу [Приложение 5] За правильные ответы раздает жетоны(см. этап4) | 1.трое учащихся выходят к доске и работают самостоятельно по карточкам, в которых написано задание. [Приложение 3]
2.Все вместе проверяют, верно ли они заполнили таблицы. 3.Выходит 2 тройка учеников к доске- строить графики по точкам, взятым из таблиц, написанных на доске. 3. Ученики приступают к работе, а весь класс занимается по таблице, отвечая на вопросы учителя [Приложение 5] 4.Подведение итогов этапа. |
| 6 | Этап проверки знаний. Самостоятельная работа, которая дается в 4 вариантах различной трудности: 1 вариант облегченный, 2 и 3 варианты средней трудности ( два варианта средней трудности для того, чтобы сидящие за одной партой не писали одинаковые варианты), 4 вариант – повышенной трудности. Какой выполнять вариант – ребята выбирают сами. | Консультирует учеников. После выполнения работы выводит на экран информацию с ответами с самостоятельной работе | Решают самостоятельную работу [Приложение 6] После выполнения работы сравнивают ответы с ответами на экране. Ставят себе отметки. |
| 7 | Этап информации о домашнем задании | На экран выводит номера домашнего задания. Обсуждает с учениками моменты выполнения домашнего задания | Записывают домашнее задание в дневник. |
| 8 | Рефлексия. Итоги урока.
| 1.Предлагает оценить степень сложности урока и усвоения материала. | 1.Высказывают свое мнение |
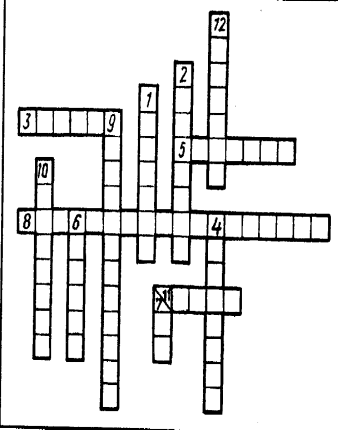
Приложение 1
Вопросы кроссворда :
Зависимость между переменными, при которой каждому значению независимой переменной соответствует единственное значение зависимой переменной.
Независимая переменная.
Множество точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – значениям функции.
Функция, заданная формулой у= кх + в
Каким коэффициентом называют число к в формуле у= кх +в.
Что служит графиком линейной функции?
Если к ¹ 0, то график у =кх +в пересекает эту ось, а если к = 0, то параллелен ей. Какой буквой эта ось обозначается?
Слово в названии функции у = кх.
Функция у = х 2
Название графика квадратичной функции.
Буква латинского алфавита, которой часто обозначают функцию.
Один из способов задания функции. (формула).
Приложение 2
Приложение 3
КАРТОЧКА1.
Заполнить таблицу (рис. 1) значений функции у =12х-5 по данным значениям ее аргумента.
Рисунок 1.
| х | 1 | 2 | 3 | 4 | 5 | 6 | 8 | 12 |
| х | 1-1 | -2 | -3 | -4 | -5 | -6 | -8 | -12 | |
| у |
|
|
|
|
|
|
|
|
| У |
|
|
|
|
|
|
|
| |
КАРТОЧКА 2.
Заполнить таблицу (рис 2) значений функции у=х 3 по данным значениям ее аргумента.
Рисунок 2.
| х | 1 | 2 | 3 | 4 |
|
|
| х | 1-1 | -2 | -3 | -4 |
| ||||||||||||
| у |
|
|
|
|
| У |
|
|
|
| |||||||||||||||
КАРТОЧКА 3.
Заполнить таблицу ( рисунок, аналогичный рис.2) значений функции у= х 2
По данным значениям ее аргумента.
Приложение 4
Вопросы, которые проецируются на экран:
1.Как называют следующие функции, заданные формулами:
у = кх; у =кх+в; у = в; у = х ; у = кх ; у= х ; у = кх ; Что является графиком данных функций ?
2.Укажите области определения следующих функций: у = х + 8 ;
У = 1/ (х - 7); у= 2х; у = 7 – 5х; У =х ; у = -10/х.
Приложение 5
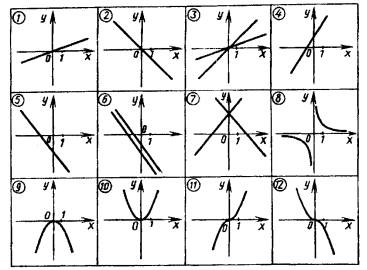
Ученики приступают к работе, а весь класс занимается по таблице рисунка 3 , отвечая на поставленные учителем вопросы:
1. На каком рисунке из таблицы изображен график:
а) линейной функции;
б) прямой пропорциональности;
в) квадратичной функции;
г) функции вида у = kx3 ?
2. Какой знак имеет коэффициент k в формулах вида у = kx + b, которым соответствуют графики на рис. 1, 2, 4, 5 таблицы ?
3. Найдите в таблице графики линейных функций, у которых угловые коэффициенты: а) равны; б) равны по модулю и противоположны по знаку.
Рисунок 3.
Приложение 6
Для примера два варианта самостоятельной работы:
ВАРИАНТ 1.
1.Дана функция у= х 2 –1. Найти значение функции у=?, при значении аргумента х=5.
Ответы: 1) 9 ; 2) 11; 3) 26; 4) 24.
2.Для функции у= 2х –9 найдите значение аргумента х при котором значение функции равно 0.
Ответы: 1)4,5 2) – 4,5 3) - 9 4) 9.
3.Какая из перечисленных формул задает обратную пропорциональность?
1.) у = 5х ; 2.) у = 5х – 1; 3.) у = 5/х; 4.) у = 5/ х 2.
ВАРИАНТ 2.
1. Дана функция у = х 2 – 5. Найти значения функции при значениях аргумента х = - 3 и х =1. Запишите сумму получившихся значений.
Ответы: 1.) 0; 2.) 8; 3.) - 13; 4.) 13.
2.Для функции у = - 0,5х + 3 найдите значение аргумента, при котором значение функции равно 1.
Ответы: 1.) 8; 2.) – 4; 3.) 4 ; 4.) ваш вариант ответа.
3.Задайте формулой обратную пропорциональность, зная, что ее график проходит через точку А(2;5.)
Ответы: 1.) у = 2/ (5х); 2.) у = 5/ (2х); 3.) у = 2,5х; 4.) у = 10 / х.
Литература:
Алтынов П.И. Алгебра 7 – 9. Тесты. Москва, «Дрофа»,1999.
Программы общеобразовательных учреждений. Алгебра. 7-9 классы./ Составитель Бурмистроваа Т.А./ - М.:«Просвещение»,2009. – 250 с.
Макарычев Ю.Н., Миндюк Н.Г. Алгебра. Учебник для 7 класса общеобразовательных учреждений. – М.: «Просвещение», 2007.-240с.
Манвелов С.Г. Конструирование современного урока математики. Книга для учителя.- М.: «Просвещение», 2002.-162с.
Селевко Г.К. Современные образовательные технологии: учебное пособие.-М.:Народное образование,1998.-256 с.
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
