Развитие пространственных представлений школьников в процессе изучения элементов геометрии в соответствии с требованиями ФГОС
Подготовила Григорьева Ирина Васильевна, учитель математики МБОУ СОШ №8 г. Приморска Калининградской области
В курсе математики 5-6 классов можно выделить следующие основные содержательные линии: арифметика; элементы алгебры; вероятность и статистика; наглядная геометрия. (Слайд 2).
Содержание линии «Наглядная геометрия» способствует формированию у учащихся первичных представлений о геометрических абстракциях реального мира, закладывает основы формирования правильной геометрической речи, развивает образное мышление и пространственные представления. (Слайд 3).
В сборнике рабочих программ по математике для 5-6 классов (составитель: Т.А. Бурмистрова. Просвещение, 2014 г.) чётко прописано содержание образования линии «Наглядная геометрия».
Наглядные представления о фигурах на плоскости: прямая, отрезок, луч, угол, ломаная, многоугольник, правильный многоугольник, окружность, круг. Четырёхугольник, прямоугольник, квадрат. Треугольник, виды треугольников. Изображение геометрических фигур. Взаимное расположение двух прямых, двух окружностей, прямой и окружности. Длина отрезка, ломаной. Периметр многоугольника. Единицы измерения длины. Измерение длины отрезка, построение отрезка заданной длины. Угол. Виды углов. Градусная мера угла. Измерение и построение углов с помощью транспортира. Понятие площади фигуры; единицы измерения площади. Площадь прямоугольника, квадрата. Равновеликие фигуры. Наглядные представления о пространственных фигурах: куб, параллелепипед, призма, пирамида, шар, сфера, конус, цилиндр. Изображение пространственных фигур. Примеры сечений. Многогранники, правильные многогранники. Примеры развёрток многогранников, цилиндра и конуса. Понятие объёма; единицы объёма.Объём прямоугольного параллелепипеда, куба. Понятие о равенстве фигур. Центральная, осевая и зеркальная симметрии. Изображение симметричных фигур. (Слайд 4).
Сравним уровень геометрического материала в 5-6 и 7 классах. (Слайд 5).
| 5-6 класс удельный вес геометрического материала составляет не более 25 %; понятийный геометрический аппарат фактически остается на уровне начальной школы; в учебниках очень мало определений (часто их заменяют описания); элементы теории даются в виде кратких объяснительных текстов, основными видами умозаключений являются индукция и аналогия, геометрический материал мало используется для формирования специальных приемов учебной деятельности. | 7 класс удельный вес геометрического материала составляет порядка 40-45%; содержание учебников и теоретический уровень изложения материала резко количественно и качественно меняются: предусматривается знакомство с 40 – 50 определениями и 20 – 30 теоремами; разобщённость планиметрии и стереометрии подавляет развитие пространственного воображения. |
Таким образом перед нами возникает задача по преодолению разрыва при изучении элементов геометрии в 5-6кл. и геометрии в 7кл. посредством знакомства учащихся 5-6кл. перед систематическим курсом со всеми объектами изучения.
Для её решения мы используем:
классно-урочную систему (уроки повторения и обобщения пройденного геометрического материала);
внеурочное время (элективные курсы по математике);
проектную деятельность. (Слайд 6).
Сравним УМК по математике 5-6 классов разных авторов относительно представленного в них геометрического материала.
Математика 5-6 класс (Дорофеев Г.В., Шарыгин И.Ф., Суворова С.Б.)
Особенности:
- целенаправленное развитие познавательной сферы учащихся, активное формирование универсальных учебных действий;
- создание условий для понимания и осознанного овладения содержанием курса;
- эффективное обучение математическому языку и знаково-символическим действиям;
- использование технологии уровневой дифференциации, которая позволяет работать в классах разного уровня, индивидуализировать учебный процесс в рамках одного коллектива.
Общими методическими идеями курса являются:
материалу на новом уровне, включать знания в новые связи, формировать их в системе;
- организация этапа содержательно-практической деятельности как исходного при введении новых понятий;
- широкое использование наглядности; - структурирование содержания «по спирали», что позволяет возвращаться к знакомому
- опора на здравый смысл и интуицию.
Все это создает условия для осознанного восприятия материала учащимися, активизации их познавательной деятельности. (Слайд 7).
По особенностям содержания курс можно охарактеризовать как арифметико-геометрический: в нем усилено внимание к изучению арифметики и представлена наглядно-деятельностная геометрия. Кроме того, начиная с 5 го класса, последовательно изучается вероятностно-статистический материал. (Слайд 8).
УМК Н.Я.Виленкина и др. и УМК В. Б. Полонского, М. С. Якира, А. Г. Мерзляка. (Слайды 9 и 10).
Из сравнительных таблиц видно, что темы практически дублируются, а количество часов, отведённых на изучение элементов геометрии, заметно отличаются.
Итак, средств и способов развития пространственных представлений школьников при изучении элементов геометрии очень много. Рассмотрим лишь некоторые из них.
1. Упражнения и задачи (условно разделим их на уровни: начальный, иллюзии и невозможные объекты, задания с использованием развертки куба, цилиндра, задания на проекции фигур).
Начальный уровень – задачи и упражнения, не требующие специальных знаний.
Например:
1. Разделите круглый сыр тремя разрезами на восемь частей.
2. Расположите пять одинаковых монет так, чтобы каждая из них касалась четырех остальных.
3. Из шести спичек сложите четыре правильных треугольника так, чтобы стороной каждого была целая спичка. (Слайд 11).
Решения к упражнениям 1-3 (слайд 12):

Иллюзии и невозможные объекты.(Слайды 13,14,15).
Например:
1. Закройте листом цветной бумаги переднюю грань куба, и опишите свои впечатления (рис.а).
2. Закройте листом цветной бумаги заднюю грань куба и постарайтесь передать свои впечатления (рис.б). На что похож рисунок: на шкафчик? полочку?

Видеть куб нам позволяет хорошо развитое пространственное воображение. Но удивительно: один раз мы видим этот куб как бы сверху и справа (рис. а), а другой — снизу и слева (рис. б).
3.На рис.а фигура не дорисована (верхняя часть изображения закрыта листом бумаги.)
Дорисуйте ее.
(Учащиеся обычно дорисовывают фигуру так, как на рис.б и не видят никакой ловушки. Она становится ясна только при взгляде на рис.в. Становится понятным, что таких фигур, как на рис.в в реальности не существует).

4. Поясните, может ли существовать не на бумаге, а в жизни фигура, показанная на рисунке.

Задания с использованием развертки куба, цилиндра. (Слайд 16,17,18).
Например:
1. Из бумаги склеили куб. Ясно, что его можно разрезать на шесть равных квадратов. А можно ли его разрезать на двенадцать квадратов?

Нетрудно доказать, что фигура, состоящая из объединения треугольников А и В , расположенных в одной плоскости, есть квадрат.
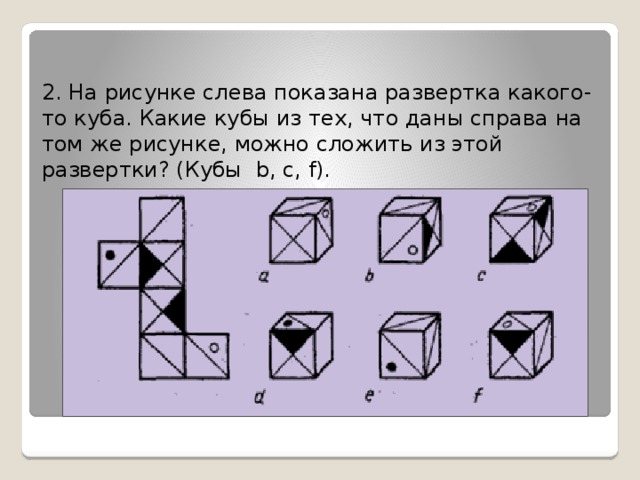
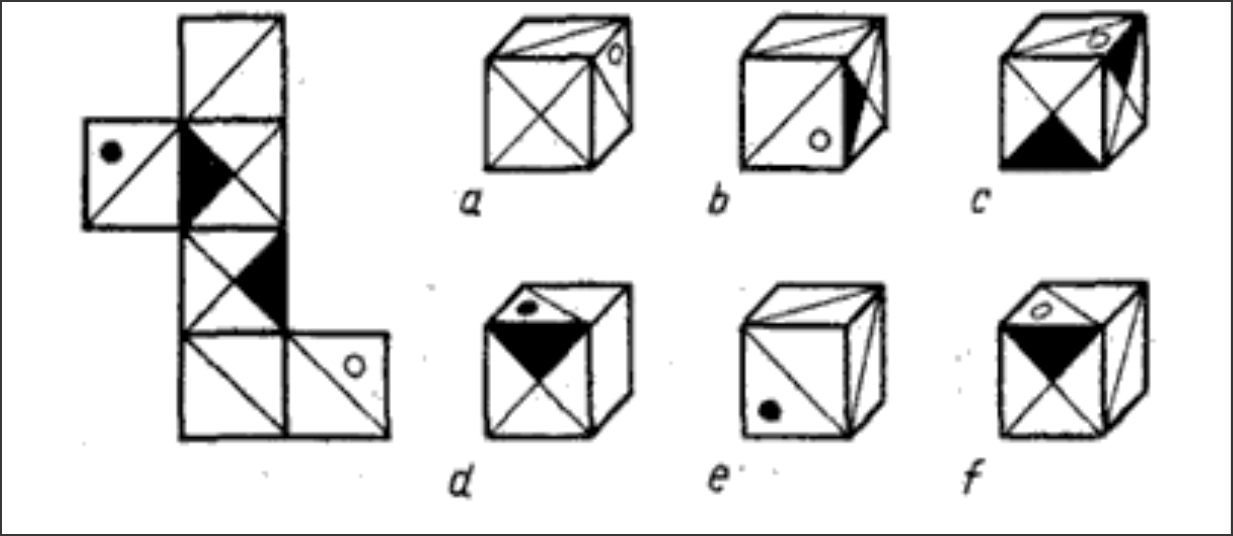
2.На рисунке слева показана развертка какого-то куба. Какие кубы из тех, что даны справа на том же рисунке, можно сложить из этой развертки? (Кубы b, с, f).
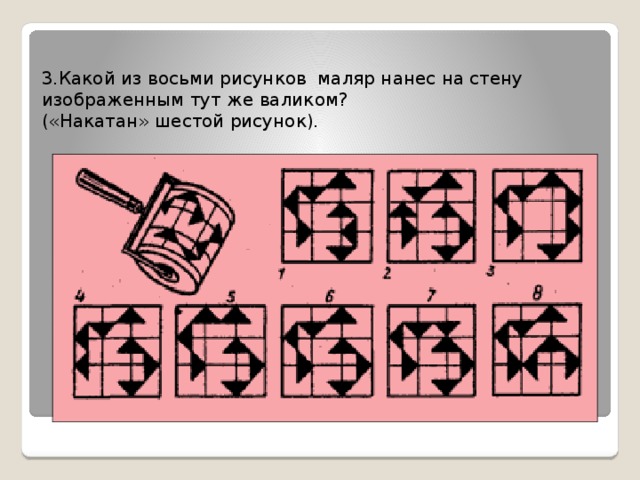
3.Какой из восьми рисунков маляр нанес на стену изображенным тут же валиком?
(«Накатан» шестой рисунок).

Задания на проекции фигур. (Слайд 19).
Например:
1. Какую форму имеет тень куба на плоскость, перпендикулярную его диагонали, от пучка лучей
света, параллельных этой диагонали? (Правильный шестиугольник).
2. На рис. а жирной линией показаны фигуры, согнутые из проволоки. Изобразите три их
проекции: на переднюю грань куба, на боковую его грань и на верхнюю грань. (Ответы на рис. б под изображениями соответствующих фигур).

Геометрические конструкторы и игры. (Слайды 20-26).
Широкое использование различных геометрических конструкторов и игр способствует развитию пространственного воображения школьников.
Например, конструктор для объёмного моделирования «ТИКО», который представляет собой скомплектованные в наборы многоугольники, которые соединяются между собой, создавая двух- и трехмерные фигуры и тела.

Можно сначала собрать плоскую фигуру, например, развертку куба, а затем перейти в пространство или объем. Поднимая грани-квадраты и соединяя их, собираем куб.

Шарнирное соединение ТИКО-деталей позволяет скреплять многоугольники под любым углом и вращать их один относительно другого.

Наличие дополнительных креплений на некоторых деталях ТИКО делает возможным их перпендикулярное соединение.

Конструктор ТИКО и его возможности в обучении: математика.
Наборы «Школьник», «Геометрия».
Педагогам конструктор полезен, как средство для быстрого создания
наглядных пособий. Из ТИКО-деталей можно сконструировать практически весь спектр геометрических фигур и тел.




Многогранники.





Конструктор ТИКО и его возможности в обучении .






Используемая литература и интернет -ресурсы:
1. Александров А.Д. О геометрии // Математика в школе. 1980. №3. -С.56-62.
2. Ананьев Б.Г., Рыбалко Е.Ф. Особенности восприятия пространства у детей. М.: Просвещение, 1964. - 304 с.
3. Верченко С.Б. Развитие пространственных представлений учащихся при изучении геометрического материала в 4-5 классах: Дисс. . канд. пед. наук. Москва, 1983.-215 с.
4. Шарыгин И.Ф., Ерганжиева JI.H. Наглядная геометрия: Учебное пособие для учащихся V-VI классов. М.: МИРОС, 1998. - 240 с.
5. http://schoolguide.ru/index.php/midschool-matem/matematika-dorofeev.html
6. http://www.tico-rantis.ru/games_and_activities/