Тема урока: Решение комбинаторных задач
Комбинаторные задачи – это задачи, в которых требуется из элементов составить различные наборы, подсчитать количество всевозможных комбинаций элементов, составленных по определённому правилу.
Методы решения комбинаторных задач:
метод перебора;
построение дерева возможных вариантов решений;
табличный метод (все условия вносятся в таблицу, в ней же выполняется решение);
правило умножения.
Метод перебора
Простые задачи решают обыкновенным полным перебором возможных вариантов без составления различных таблиц и схем.
Способ перебора может применяться в простых задачах, например в
таких, как эта:
Задача 1. Для своих двух книг Маша купила три разные обложки. Сколькими различными способами она может обернуть книги купленными обложками?
Решение: Для решения обозначим обложки буквами а, б, в. Составим из букв всевозможные пары: аб, ав, бв, ба, ва, вб. Всего получилось 6 способов.
Ответ: 6 способов.
Задача 2.
Сколько двузначных числа можно составить из цифр 1, 2, 3, 4, 5?
Решение: 11, 12, 13, 14, 15, 21, 22, 23, 24, 25, 31, 32, 33, 34, 35, 41, 42, 43,
44, 45, 51, 52, 53, 54, 55.
Ответ: 25 чисел.
Задача 3.
В финальном забеге на 100 м участвуют Иванов, Громов и Орлов. Сколько существует возможных вариантов распределения призовых мест.
Решение:
Вариант 1: 1) Иванов, 2) Громов, 3) Орлов.
Вариант 2: 1) Иванов, 2) Орлов, 3) Громов.
Вариант 3: 1) Орлов, 2) Иванов, 3) Громов.
Вариант 4: 1) Орлов, 2) Громов, 3) Иванов.
Вариант 5: 1) Громов, 2) Орлов, 3) Иванов.
Вариант 6: 1) Громов, 2) Иванов, 3) Орлов.
Ответ: 6 вариантов.
Метод построения дерева возможных вариантов решений
Подбирая различные комбинации, можно запутаться. В этом случае приходит на помощь метод построения дерева возможных вариантов решений. Внешне такая схема напоминает дерево, отсюда и название.
Если его правильно построить, ты не упустишь ни один из возможных вариантов решения.
Рассмотрим задачу 1. Учитель попросил Олега разложить на полке 3 шара - желтый, красный, синий. Сколькими способами Олег может это сделать?
Начать можно и с желтого, и с красного, и с синего шара. Дерево вариантов будет выглядеть так:
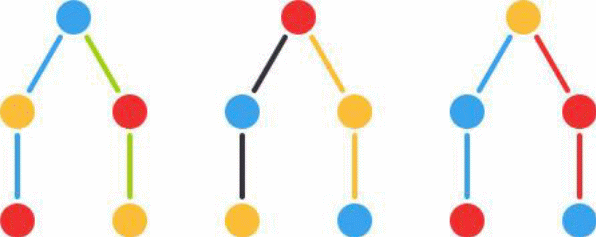
Эта схема действительно похожа на дерево, правда, «вверх ногами» и без ствола. Каждый первый шар - это «корень» дерева, а ветви дерева - это различные варианты расположения шаров. По этой схеме несложно посчитать, что возможных комбинаций всего 6.
Ответ: 6 способов.
Схему-дерево возможных рассуждений можно располагать по-разному (корень вверху или внизу).
Табличный метод
Решить комбинаторные задачи можно с помощью таблиц. Они, как и дерево возможных вариантов, наглядно представляют решение таких задач.
Задача 1. Сколько нечетных двузначных чисел можно составить из цифр 1, 3, 4, 6, 7, 8, 9?
Решение. Составим таблицу: слева первый столбец - первые цифры искомых чисел, вверху первая строка - вторые цифры.
|
| 1 | 3 | 7 | 9 |
| 1 | 11 | 13 | 17 | 19 |
| 3 | 31 | 33 | 37 | 39 |
| 4 | 41 | 43 | 47 | 49 |
| 6 | 61 | 63 | 67 | 69 |
| 7 | 71 | 73 | 77 | 79 |
| 8 | 81 | 83 | 87 | 89 |
| 9 | 91 | 93 | 97 | 99 |
Ответ: 28.
Задача 2. Маша, Оля, Вера, Ира, Андрей, Миша и Игорь готовились стать ведущими на Новогоднем празднике. Назовите возможные варианты, если ведущими могут быть только одна девочка и один мальчик.
Решение. Составим таблицу: слева первый столбец - имена девочек, вверху первая строка - имена мальчиков.
|
| Андрей | Миша | Игорь |
| Маша | Маша – Андрей | Маша – Миша | Маша – Игорь |
| Оля | Оля – Андрей | Оля – Миша | Оля – Игорь |
| Вера | Вера – Андрей | Вера – Миша | Вера – Игорь |
| Ира | Ира – Андрей | Ира – Миша | Ира – Игорь |
Ответ: Все возможные варианты перечисляются в строках и столбцах таблицы. Всего 12 вариантов.
Задача 3. В школьной столовой приготовили на завтрак плов (П), кашу (К), блины (Б), а из напитков – сок (С), чай (Ч) и молоко (М). сколько различных вариантов завтрака можно составить?
|
| П | К | Б |
| С | СП | СК | СБ |
| Ч | ЧП | ЧК | ЧБ |
| М | МП | МК | МБ |
Ответ: 9 вариантов.
Правило умножения
Применяется для нахождения числа всех возможных исходов независимого проведения двух испытаний А и В, перемножив число всех исходов испытания А и число всех исходов испытания В.
Задача.
Сколько трехзначных чисел можно составить из цифр: 1, 2, 5, 8 используя в записи числа каждую из них не более одного раза?
Решение:
Первую цифру выбираем четырьмя способами (1, 2, 5, 8), вторую цифру можно выбрать тремя способами, и на выбор третьей цифры остается два способа. Количество искомых трехзначных чисел равно произведению 4 · 3 · 2 = 24.
Ответ: 24.
ЗАДАНИЕ:
Просмотрите презентацию по теме урока.
Изучите данный теоретический материал и сделайте краткий опорный конспект по теме урока.
Решите задания по теме урока.
В финальном забеге на 100 м участвуют Смирнов, Петров и Орлов. Назовите возможные варианты распределения призовых мест. (Решить, используя табличный метод)
В столовой предлагают два первых блюда: щи и борщ; три вторых блюда: рыба, гуляш и плов; два третьих: компот и чай. Перечислите все возможные варианты обедов из трех блюд. Проиллюстрируйте ответ, построив дерево возможных вариантов.
Сколько трехзначных чисел можно составить из цифр: 1, 2, 5, 8 используя в записи числа каждую из них не более одного раза?
(Решить по правилу умножения)
ОТЧЕТ:
Опорный конспект.
Решение заданий из п.3


















