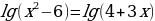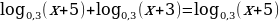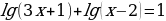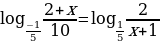Просмотр содержимого документа
«Решение логарифмических уравнений»
Практическое занятие
Решение логарифмических уравнений
1) Подготовительный этап.
Перепишите и заполните пропуски:
Пример 1. Решите уравнение: 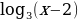 = 3
= 3
Решение: по определению логарифма получаем уравнение: х – 2 = 33, х – 2 = …, х = 27 + 2,
х = …
Проверка: при х = 29, 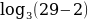 = 3 – верно
= 3 – верно
Ответ: х = 29
Пример 2. Решите уравнение: 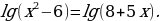
Решение:
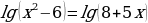
Приравниваем подлогарифмические выражения: 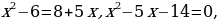
D = (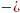 5)2
5)2 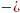 4
4 1
1 (
( ) = 25 + 56 = …, Х 1=
) = 25 + 56 = …, Х 1= 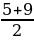 = …, Х2 =
= …, Х2 = 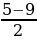 =
= 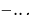
Проверка: при х = 7, 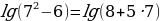 - верно
- верно
при х = - 2, 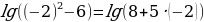 - неверно
- неверно
Ответ: x = 7
Пример 3. Решите уравнение 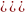 Решение: Используем метод - решение логарифмических уравнений заменой.
Решение: Используем метод - решение логарифмических уравнений заменой.
Пусть 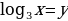 . Тогда уравнение примет вид: у2 – 4у + 4 = 0, D = (- 4)2 - 4 ∙1 ∙ 4 = 16 - … = 0, у =
. Тогда уравнение примет вид: у2 – 4у + 4 = 0, D = (- 4)2 - 4 ∙1 ∙ 4 = 16 - … = 0, у = 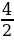 = ... . Делаем обратную замену:
= ... . Делаем обратную замену: 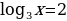 . Тогда по определению логарифма получаем, что х = 32, х = …
. Тогда по определению логарифма получаем, что х = 32, х = …
Ответ: х = 9
Пример 4. Решите уравнение: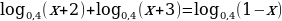
Решение:
Воспользовавшись правилом сложения логарифмов, переходим к равносильному в области допустимых значений уравнению: 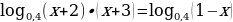
Основания логарифмов одинаковы, поэтому можно перейти к следующему уравнению:
(х + 2)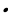 (х + 3) = 1
(х + 3) = 1 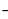 х, х2 + 3х + 2х + 6 – 1 + х = 0, х2 + 6х + 5 = 0,
х, х2 + 3х + 2х + 6 – 1 + х = 0, х2 + 6х + 5 = 0,
D = (6)2 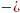 4
4 1
1 5= 36 – 20 = …, Х 1 =
5= 36 – 20 = …, Х 1 = 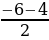 =
=  , Х2 =
, Х2 = 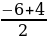 = –....
= –....
Проверка: при х = – 5, 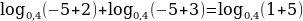 - неверно
- неверно
при х = – 1, 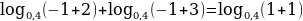 - верно
- верно
Ответ: x = – 1
Пример 5. Решите уравнение: 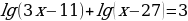
Решение:
Перепишем исходное уравнение, используя свойства суммы логарифмов. Получим следующее уравнение: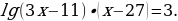 По определению логарифма получим уравнение:
По определению логарифма получим уравнение:
(3х 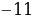 )
)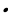 (х
(х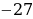 ) =
) =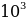 ,
, 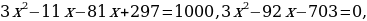
Найдем корни полученного квадратного уравнения:
D = (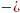 92)2
92)2  4
4 1
1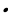 (
(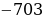 ) = 8464 + 8436 = …,
) = 8464 + 8436 = …,
Х1= 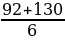 =
= 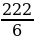 = …, Х2 =
= …, Х2 = 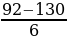 =
= 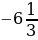 .
.
Проверка: при х = 37, 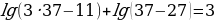 - верно
- верно
при х = 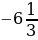 ,
, 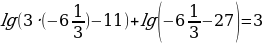 - неверно
- неверно
Ответ: х = 37
2) Практический этап.
Вариант 1 Вариант 2
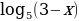 = 2
= 2
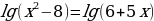
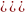
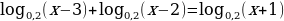
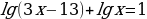
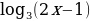 = 2
= 2
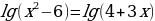
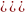
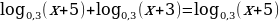
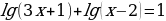
3) Дополнительные задания*
Решите уравнение.
lg(х – 1)2 = 0
log2 log3 Х = 1
log3 log2 log2 Х = 0
log2 log3 Х2 = 2
lgХ = 2 – lg5
lg Х – lg11 = lg19 – lg(30 – Х)
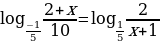
log3(x2 – 4x + 3) = log3(3x + 21)
log2(9 – 2x) = 3 – x
log3(Х – 2) + log3 Х = log38
log22Х + 3 = 2 log2 Х2
lg2x2 – 10 lgx + 1 = 0
log4(x + 3) – log4(x – 1) = 2 – log48
0,5 lg(2x – 1) + lg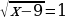
logx+1(x2 – 3x + 1) = 1







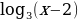 = 3
= 3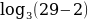 = 3 – верно
= 3 – верно 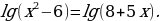
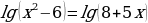
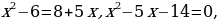
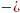 5)2
5)2 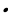 1
1 ) = 25 + 56 = …, Х 1=
) = 25 + 56 = …, Х 1= 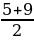 = …, Х2 =
= …, Х2 = 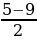 =
= 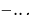
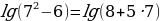 - верно
- верно 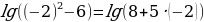 - неверно
- неверно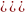 Решение: Используем метод - решение логарифмических уравнений заменой.
Решение: Используем метод - решение логарифмических уравнений заменой.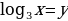 . Тогда уравнение примет вид: у2 – 4у + 4 = 0, D = (- 4)2 - 4 ∙1 ∙ 4 = 16 - … = 0, у =
. Тогда уравнение примет вид: у2 – 4у + 4 = 0, D = (- 4)2 - 4 ∙1 ∙ 4 = 16 - … = 0, у = 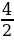 = ... . Делаем обратную замену:
= ... . Делаем обратную замену: 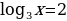 . Тогда по определению логарифма получаем, что х = 32, х = …
. Тогда по определению логарифма получаем, что х = 32, х = … 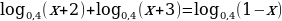
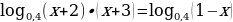
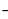 х, х2 + 3х + 2х + 6 – 1 + х = 0, х2 + 6х + 5 = 0,
х, х2 + 3х + 2х + 6 – 1 + х = 0, х2 + 6х + 5 = 0, 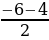 =
=  , Х2 =
, Х2 = 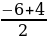 = –....
= –.... 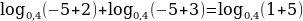 - неверно
- неверно 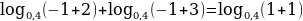 - верно
- верно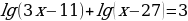
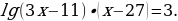 По определению логарифма получим уравнение:
По определению логарифма получим уравнение: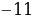 )
)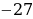 ) =
) =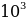 ,
, 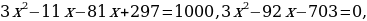
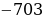 ) = 8464 + 8436 = …,
) = 8464 + 8436 = …, 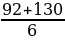 =
= 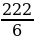 = …, Х2 =
= …, Х2 = 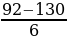 =
= 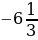 .
. 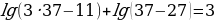 - верно
- верно 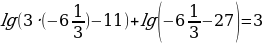 - неверно
- неверно 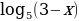 = 2
= 2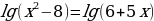
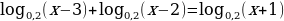
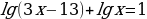
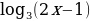 = 2
= 2