Россия, ДНР, Макеевка
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 20.11.2024 17:22
Винникова Ирина Александровна
учитель математики
64 года
383
107 158 
Местоположение
Специализация
Решение неравенств второй степени
Категория:
Алгебра
31.01.2024 16:41
Просмотр содержимого документа
«Решение неравенств второй степени»
РЕШЕНИЕ НЕРАВЕНСТВ ВТОРОЙ СТЕПЕНИ С ОДНОЙ ПЕРЕМЕННОЙ
9 классс
Три пути ведут к знаниям: путь размышления – это путь самый благородный.
Путь подражания – самый легкий.
Путь опыта – самый горький.
Конфуций
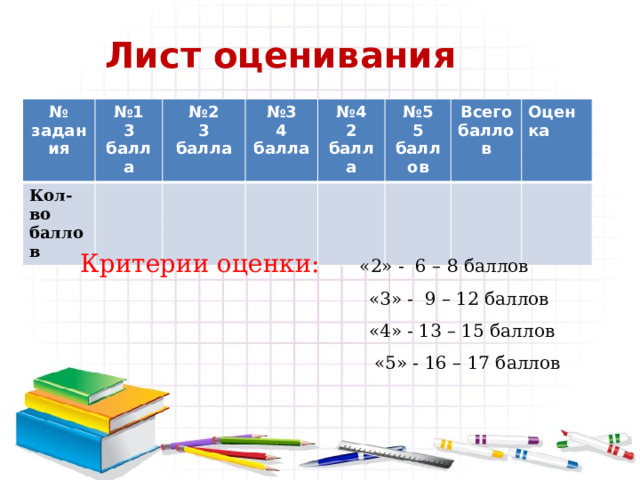
Лист оценивания
№ задания
№ 1
Кол-во баллов
3 балла
№ 2
3 балла
№ 3
4 балла
№ 4
№ 5
2 балла
5 баллов
Всего баллов
Оценка
Критерии оценки: «2» - 6 – 8 баллов
«3» - 9 – 12 баллов
«4» - 13 – 15 баллов
«5» - 16 – 17 баллов
Какие неравенства называются неравенствами второй степени с одной переменной?
ОПРЕДЕЛЕНИЕ
Неравенства вида ()где х - переменная, а, в, с –некоторые числа и а≠0, называют неравенствами второй степени с одной переменной (квадратными неравенствами).
Из предложенных неравенств выберите квадратные:
1)
2)
3)
4)
5)
6)
Что называется решением неравенства второй степени с одной переменной?
Что значит решить неравенство?
Определение
Значение переменной при котором данное неравенство обращается в верное числовое неравенство, называется решением неравенства.
Решить неравенство- значит найти все его решения или доказать, что их нет.
Назовите методы решения неравенств второй степени с одной переменной?
0: (-∞;1)U (3;+∞) у у=0: х= -1 у0: (-∞;-1)U (-1;+∞) у у х х 1 0 3 0 -1 у=0: х=-3; 1 у0: (-3;1) у у 2) 1) у у 3 х 0 х 0 1 -3 4) 3) " width="640"
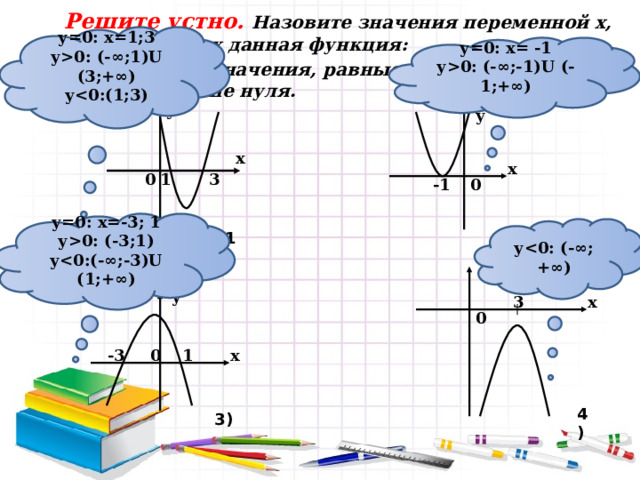
Решите устно. Назовите значения переменной х, при которых данная функция:
а) принимает значения, равные нулю; больше нуля; меньше нуля.
у=0: х=1;3
у 0: (-∞;1)U (3;+∞)
у
у=0: х= -1
у0: (-∞;-1)U (-1;+∞)
у
у
х
х
1
0
3
0
-1
у=0: х=-3; 1
у0: (-3;1)
у
у
2)
1)
у
у
3
х
0
х
0
1
-3
4)
3)
или ) или ниже оси х (если решают неравенство со знаком " width="640"
Алгоритм решения неравенств второй степени с одной переменной графически
- найти дискриминант квадратного трёхчлена
и выяснить, имеет ли трёхчлен корни (найти нули функции);
- на оси х отмечают корни, если они есть, и проводят схематически параболу с учётом направления её ветвей;
- находят на оси х промежутки, для которых точки параболы расположены выше (если решают неравенство со знаком или ) или ниже оси х (если решают неравенство со знаком
Алгоритм решения неравенств методом интервалов
- Определим соответствующую функцию
- Найдем нули функции при f(х)=0 и отметим на координатной прямой.
- В каждом из промежутков на которые область определения разбивается нулями функции , знак функции сохраняется, а при переходе через нуль ее знак меняется. Определим знаки , используя свойство чередования знаков, двигаясь по координатной прямой справа налево .
Гимнастика для глаз
0 (-∞;1] U [7;+∞) х²+3х≤0 (-∞;-2) U (2;+∞) х²-8х+7≥0 (-15;7) (х-7)(х+15)" width="640"
Сопоставить неравенство и его решение
х²-40 (-∞;1] U [7;+∞)
х²+3х≤0 (-∞;-2) U (2;+∞)
х²-8х+7≥0 (-15;7)
(х-7)(х+15)
0; Ученик. Решение. а) (х + 2)(х – 7) 0 Найдем нули функции у = (х + 2) (х – 7). (х + 2)(х -7) = 0 + - + Х + 2 = 0 или х – 7 = 0 - 2 7 Х = -2 х = 7 Ответ: (-2; 7) " width="640"
Найди ошибку
1. Решите неравенства методом интервалов
а) (х + 2) (х – 7) 0;
Ученик.
Решение.
а) (х + 2)(х – 7) 0
Найдем нули функции у = (х + 2) (х – 7).
(х + 2)(х -7) = 0 + - +
Х + 2 = 0 или х – 7 = 0 - 2 7
Х = -2 х = 7
Ответ: (-2; 7)
![б)(х – 5) (х + 3)≤0 Решение. Найдем нули функции f(х)= (х – 5) (х + 3) (х – 5) (х + 3) = 0 х – 5 = 0 или х + 3 = 0 х = 5 х = - 3 + - + -3 5 Ответ: ( -3; 5). Правильный ответ: [-3; 5].](https://fsd.multiurok.ru/html/2024/01/31/s_65ba4c33740f1/img15.jpg)
б)(х – 5) (х + 3)≤0
Решение.
Найдем нули функции f(х)= (х – 5) (х + 3)
(х – 5) (х + 3) = 0
х – 5 = 0 или х + 3 = 0
х = 5 х = - 3
+ - +
-3 5
Ответ: ( -3; 5).
Правильный ответ: [-3; 5].
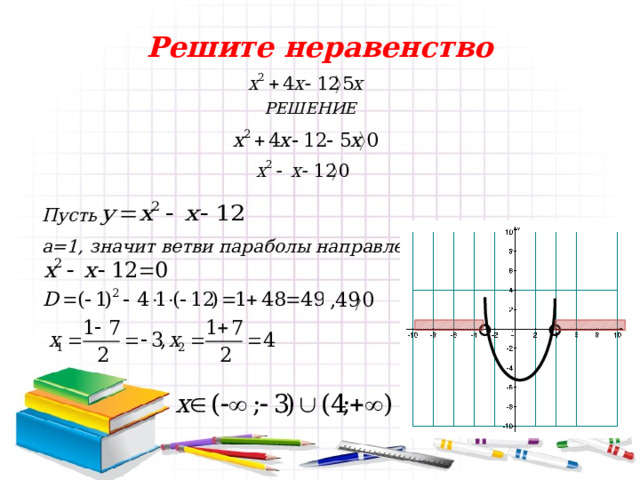
Решите неравенство
РЕШЕНИЕ
Пусть
а=1, значит ветви параболы направлены вверх.
Тест
Проверь соседа
1 вариант. 2 вариант.
а а
г в
г а
б г
в б
Домашнее задание
Повторить п.14, 15
№ 378, 388, 393
Анкета самоанализа
Настоящий ученик умеет выводить известное из неизвестного и этим приближается к учителю.
Гете И.В. (1749-1832)
Критерии оценки: «2» - 6 – 8 баллов
«3» - 9 – 12 баллов
«4» - 13 – 15 баллов
«5» - 16 – 17 баллов
В заключение урока:
- «Музыка может возвышать или умиротворять душу,
- Живопись – радовать глаз,
- Поэзия – пробуждать чувства,
- Философия – удовлетворять потребности разума,
- Инженерное дело – совершенствовать материальную сторону жизни людей,
- А математика способна достичь всех этих целей»
Морис Клайн
Спасибо за внимание!
© 2024, Винникова Ирина Александровна 115 0
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
