Приглашаем на олимпиады для учителей, учеников и дошкольников. Специальные наградные, результаты сразу, всегда новые задания.

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Была в сети 21.04.2025 18:18

Моргун Александра Ивановна

Учитель математики и информатики

34 года

19 296

1 560

Подписчики

Подписки

Местоположение

Россия, Черноморское

Специализация

Информатика

Математика

Классному руководителю

Алгебра

Геометрия

Обо мне Блог Файлы Тесты Галерея Активность Награды

Решение неравенств второй степени с одной переменной.

Категория: Алгебра

28.11.2018 08:39

Учебник: Алгебра. 9 класс. Учебник. Макарычев Ю.Н., Миндюк Н.Г. и др. 21-е изд. - М.: 2014.— 271 с.

Тема: 14. Решение неравенств второй степени с одной переменной

Решение неравенств второй степени с одной переменной

Цели урока:

обучения:

Повторить и систематизировать ранее изученные способы решения неравенств второй степени;
Изучить новый способ решения неравенств второй степени;
Продолжить формирование навыков и умений анализировать и делать выводы.

развития

развитие внимания, памяти, речи, логического мышления, самостоятельности;

воспитания

воспитание дисциплины, наблюдательности, аккуратности, чувства ответственности;

Просмотр содержимого документа
«Решение неравенств второй степени с одной переменной.»

План – конспект урока (МБОУ «Черноморская средняя школа №2»)

ФИО учителя	Моргун А. И.
Предмет	Алгебра
Дата проведения урока	28.11.2018
№ урока	35
Класс	9 – А
Тема урока (в соответствии с КТП)	Решение неравенств второй степени с одной переменной
Целеполагание	Цели урока: обучения: Повторить и систематизировать ранее изученные способы решения неравенств второй степени; Изучить новый способ решения неравенств второй степени; Продолжить формирование навыков и умений анализировать и делать выводы. развития развитие внимания, памяти, речи, логического мышления, самостоятельности; воспитания воспитание дисциплины, наблюдательности, аккуратности, чувства ответственности;
Тип урока	изучение новой темы
Планируемые результаты	Предметные: формирование потребности приобретения новых знаний; развитие математической речи при комментировании решения; закрепление и углубление материала в процессе решения различных задач по теме. Личностные: готовность и способность к саморазвитию и самообучению, дисциплинированность, внимательность, трудолюбие и упорство в достижении поставленных целей, уважительное отношение к иному мнению. Метапредметные: самостоятельно создавать алгоритмы деятельности при решении проблем творческого и поискового характера, выбирать наиболее эффективные способы решения задач в зависимости от конкретных условий, уметь самостоятельно рефлексировать способы и условия действий, контролировать и оценивать процесс и результат деятельности; уметь слушать партнеров в процессе решения задач, оформлять решение в устной и письменной форме, уметь с достаточной полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации; уметь осуществлять самоконтроль, саморегуляцию, ставить цель, оценивать результат собственной деятельности.
Понятия	неравенства второй степени
Оборудование	«Алгебра, 9 » Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков под редакцией С.А. Теляковского.
Ход урока I этап -актуализация знаний -постановка темы -постановка цели -формирование УУД: Познавательные Регулятивные Коммуникативные Личностные		I. Организационный момент II. Проверка домашнего задания III. Актуализация знаний Ребята, сегодня мы рассмотрим ещё один способ решения неравенств второй степени с одной переменной: с использованием графика квадратичной функции. Для этого вспомним ещё раз основные понятия, связанные с ней. (проводится фронтальный опрос) Какая функция называется квадратичной? Что является графиком квадратичной функции? Как определить направление ветвей параболы? Что такое нули функции? Как найти нули функции?
IIэтап - изучение нового -первичное закрепление В том числе самостоятельная работа взаимопроверка		III. Изучение нового материала Решение неравенства второй степени с одной переменной можно рассматривать как нахождение промежутков, в которых соответствующая квадратичная функция принимает положительные или отрицательные значения. Например: 5х²+ 9х - 2 0. Рассмотрим функцию у = 5х²+ 9х - 2. Графиком этой функции является парабола, ветви которой направлены вверх. Выясним, как расположена эта парабола относительно оси х. Нули функции: 5х²+ 9х - 2 = 0, Д = 121, х₁ = 0,2; х₂ = -2. Построим схематически параболу в координатной плоскости 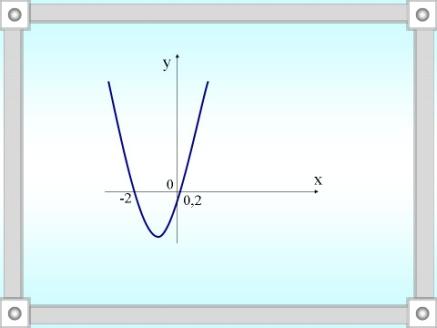Из рисунка видно, что функция принимает отрицательные значения на промежутке (-2; 0,2). Следовательно, множеством решений неравенства является промежуток (-2; 0,2). Ответ: (-2; 0,2). -х²+ 8х - 16 Графиком функции у = -х²+ 8х - 16 является парабола, ветви которой направлены вниз. Нули функции: -х²+ 8х - 16 = 0. - (х – 4)² = 0 х = 4. Из рисунка видно, что функция принимает отрицательные значения на промежутках (- ∞; 4) и (4; + ∞). Ответ: х – любое число, не равное 4. 3) х²- 3х+ 4 0. Рассмотрим функцию у = х²- 3х + 4. Графиком функции является парабола, ветви которой направлены вверх. Нули функции: х²- 3х + 4 = 0, Д = 9 -16 = -7. Д корней нет. Из рисунка видно (слайд 7), что функция принимает положительные значения при любом значении х. Ответ: х – любое число. Ребята вместе с учителем делают вывод: Итак, для решения неравенств вида ах²+ bх + с 0 и ах²+ bх + с поступают следующим образом: 1) находят дискриминант квадратного трехчлена и выясняют, имеет ли трехчлен корни; 2) если трехчлен имеет корни, то отмечают их на оси х и через отмеченные точки проводят схематически параболу, ветви которой направлены вверх при а 0 или вниз при а ; если трехчлен не имеет корней, то схематически изображают параболу, расположенную в верхней полуплоскости при а 0 или в нижней при а 3) находят на оси х промежутки, для которых точки параболы расположены выше оси х (если решают неравенство ах²+ bх + с 0) или ниже оси х (если решают неравенство aх²+ bх + с ). IV. Первичное закрепление знаний Стр. 90 № 304, 305
IIIэтап -подведение итогов		Какова была цель нашего урока? – Сформулируйте определение неравенств второй степени с одной переменной. – Как решать такие неравенства? – Алгоритм решения.
Рефлексия
Домашнее задание		П. 14 № 306, 307