Россия, Альметьевск
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 18.10.2023 00:50
Воробьева Вера Николаевна
учитель математики
63 года
696
78 912 
Местоположение
Специализация
Решение нестандартных задач
Категория:
Математика
24.10.2019 21:13
Просмотр содержимого документа
«Решение нестандартных задач»
Муниципальное бюджетное образовательное учреждение
«Средняя общеобразовательная школа №24» г. Альметьевска.
Воробьева Вера Николаевна
Урок
по теме:
«Решение нестандартных задач»
9 класс
Цели:
Образовательные
Вовлекать учащихся в совершенствование основных мыслительных операций, развивать умения самостоятельно применять знания в измененных нестандартных условиях
Развивающие
Организовать познавательную деятельность учащихся с использованием информационных ресурсов
Воспитательные
Воспитание конкурентно-способной личности, формирование мобильности и воспитание самости (т.е. самовоспитания и самообучения).
Задачи урока:
Учить рассуждать, учить мыслить, формировать интеллектуальные умения, работать в заданном темпе, выделять главное, обобщать, обсуждать проблему урока.
Оборудование:
ПК, мультимедийный проектор.
Ход урока.
«Трудность решения в какой – то мере
входит в само понятие задачи:
там где нет трудности, нет и задачи».
Д. Пойа
Тема нашего урока: «Решение нестандартных задач». Вам было дано задание просмотреть и по возможности решить нестандартные задачи. Те, кто справился с решением данных задач, подготовил презентацию. Разберем решение задачи №1.
Ваня задумал простое трехзначное число, все цифры которого различны. На какую цифру оно может оканчиваться, если его последняя цифра равна сумме первых двух?
Решение.
Обозначим задуманное трехзначное число 
. По условию с = a+b. Цифры, с помощью которых можно записать число: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. с≠2,c≠3,c≠4,c≠5,c≠6, c≠8,c≠9,c≠0.
При с = 3, с = 9 задуманное число составное. Если c =1, то 1=1+0 (не возможно) т.к. все цифры не различны. Если c=7, то 7=3+4 все цифры различны. Число оканчивается на цифру 7.
Решение задачи №2.
Существует ли десятизначное число, делящееся на 11, в записи которого использованы все цифры от 0 до 9?
Решение.
Чтобы решить данную задачу, вспомним признак делимости на число 11.
Если разность между суммой цифр, стоящих на нечётных местах, и суммой цифр, стоящих на чётных местах, в числе делится на 11, то данное число делится на 11.
Распределим цифры: 1, 2, 3, 4, 6, 7, 8, 9 на две группы так, чтобы сумма цифр первой группы была равна сумме цифр второй группы. Добавим цифры 5 и 0 в разные группы;
Сумма цифр первой группы больше суммы цифр второй группы на 5. Увеличим сумму цифр первой группы на 3, поменяв местами цифры 6 и 3. Сумма цифр в первой группе больше суммы цифр во второй группе на 11,= что цифры первой группы могут стоять на нечётных местах, а цифры второй группы – на чётных местах. Значит десятизначное число, делящееся на 11, в записи которого использованы все цифры от 0 до 9 существует.
А вот еще один способ решения этой задачи.
Пусть это число существует, т.е. число, которое делится на 11. Обозначим сумму цифр одной группы через x, а другой группы через x+11. Сумма всех цифр числа равна x+x+11, а по условию 45(т.к. 9+8+7+6+5+4+3+2+1+0=45).
Составляем уравнение:
x+x+11=45, x=17.
17- сумма цифр одной группы, x+11=28 – сумма цифр другой группы, 28-17=11.
Значит десятизначное число, делящееся на 11, в записи которого использованы все цифры от 0 до 9 существует.
Решение задачи №3.
В выпуклом шестиугольнике ABCDEF A + B + C = D + E + F
Докажите, что две противоположные стороны шестиугольника параллельны.
Доказательство.
П
роведём секущую, пересекающую отрезки CD и AF в точках M и N, и введём обозначение углов, показанные на рисунке. ABCMN и MDEFN – пятиугольники, получившиеся после сечения. Они имеют одинаковую сумму внутренних углов, т.к.
A + B + C = D + E + F по условию, то
С другой стороны,
0.
Сложим эти равенства почленно, получим:
А это внутренние накрестлежащие углы при прямых СD и АF и секущей МN.
Следовательно СD II АF.
Еще один способ решения этой задачи.
Предположим, что прямые СD и АF пересекаются в точке X. Пусть X лежит на луче АF.Сумма внутренних углов четырехугольника АBCX равна 360 0 , поэтому
A + B + C+ X = 360 0 . Сумма углов многоугольника находится по формуле
(n-2)·180 0 , следовательно сумма углов шестиугольника АBCDEF равна 7200 т.е. A + B + C +D + E + F= 2(A + B + C ) = 7200 , и значит A + B + C = 3600 . Из полученных равенств следует, что X = 00, т.е. CD II АF.
Физкультминутка
Решение задачи №4.
На каждой грани куба записали натуральное число, а в каждой вершине – произведение трех чисел, записанных на гранях, содержащих эту вершину. Сумма всех чисел, записанных в вершинах куба, оказалась равной 30. Чему равна сумма всех чисел, записанных на гранях?
Решение.
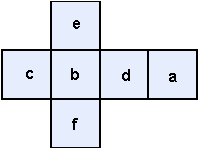
Пусть a и b, c и d, e и f – пары чисел, записанных на противоположных гранях куба. Запишем произведения трёх чисел, записанных на гранях, содержащих эту вершину:
fbc, fbd, fda, fca, ebd, eda, eac, ecb.
Найдем сумму всех чисел, записанных в вершинах куба:
fbc+fbd+fda+fca+ebd+eda+eac+ecb = f(bc+bd+da+ca)+e(bd+da+ac+cb) = f(b(c+d)+a(c+d))+e(d(b+a)+c(a+b)) = f(c+d)(b+a)+e(c+d)(b+a) = (f+e)(c+d)(b+a).
Эта сумма по условию задачи равна 30, т.е.: (f+e)(c+d)(b+a) = 30. Все рассматриваемые числа – натуральные, поэтому значение каждой из скобок не меньше 2. Число 30 можно разложить на простые множители: 30 = 2·3·5. Следовательно, (f+e)(c+d)(b+a) = 2·3·5.
Значит, сумма чисел, записанных на противоположных гранях, равна a+b+c+d+e+f = 2+3+5 = 10.
В чем заключается красота решения этой задачи? (В том, что геометрическая задача решается алгебраическим способом).
Разберем решение задачи №5.
М
ожно ли расставить шесть различных чисел вдоль шести ребер тетраэдра (по одному числу на каждое ребро) так, чтобы сумма чисел, соответствующих любым трем ребрам, сходящимся в одной вершине, была бы одинаковой?
Решение.
Обозначим числа вдоль ребер тетраэдра так, как показано на рисунке. Предположим что задача имеет решение. Сумма ребер сходящихся в одной вершине равна a+b+c, в другой вершине: a+d+e, в третьей вершине: b+d+f, в четвертой вершине:f+c+e. Тогда a+b+c = a+d+e, откуда b+c = d+e. (1). Аналогично находим суммы чисел сходящихся к другим двум вершинам, b+d+f = f+c+e, откуда b+d = c+e (2). Складывая два полученных равенства - (1) и (2), находим:
b+c = d+e
b+d = c+e
2b+c+d = 2e+c+d, 2b = 2e, b = e, получили противоречие, поскольку все шесть чисел должны быть различными.
Вывод: 6 различных чисел вдоль 6 ребер тетраэдра расставить нельзя.
Ребята, все эти задачи были предложены на городских олимпиадах в 8-10 классах за прошлые годы. Мы убедились, что рассуждая логически, применяя обычные знания в нестандартных ситуациях, можно решить любую задачу.
Домашнее задание: подберите нестандартные задачи, которые решаются обычными способами. Мне хотелось бы закончить урок словами Д. Пойа
«Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их!»
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
