"Решение полных квадратных уравнений"

Предметные

Метапредметные

Личностные

научатся

получат возможность научиться

находить дискриминант квадратного уравнения, исследовать количество корней квадратного уравнения в зависимости от знака дискриминанта, решать квадратные уравнения.

специальным приёмами решения уравнений;

уверенно применять аппарат уравнений для решения разнообразных задач из математики, смежных предметов, практики;

Развивать понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.

Наличие мотивации к познанию, учебе.

Значимость приобретаемых на уроках знаний

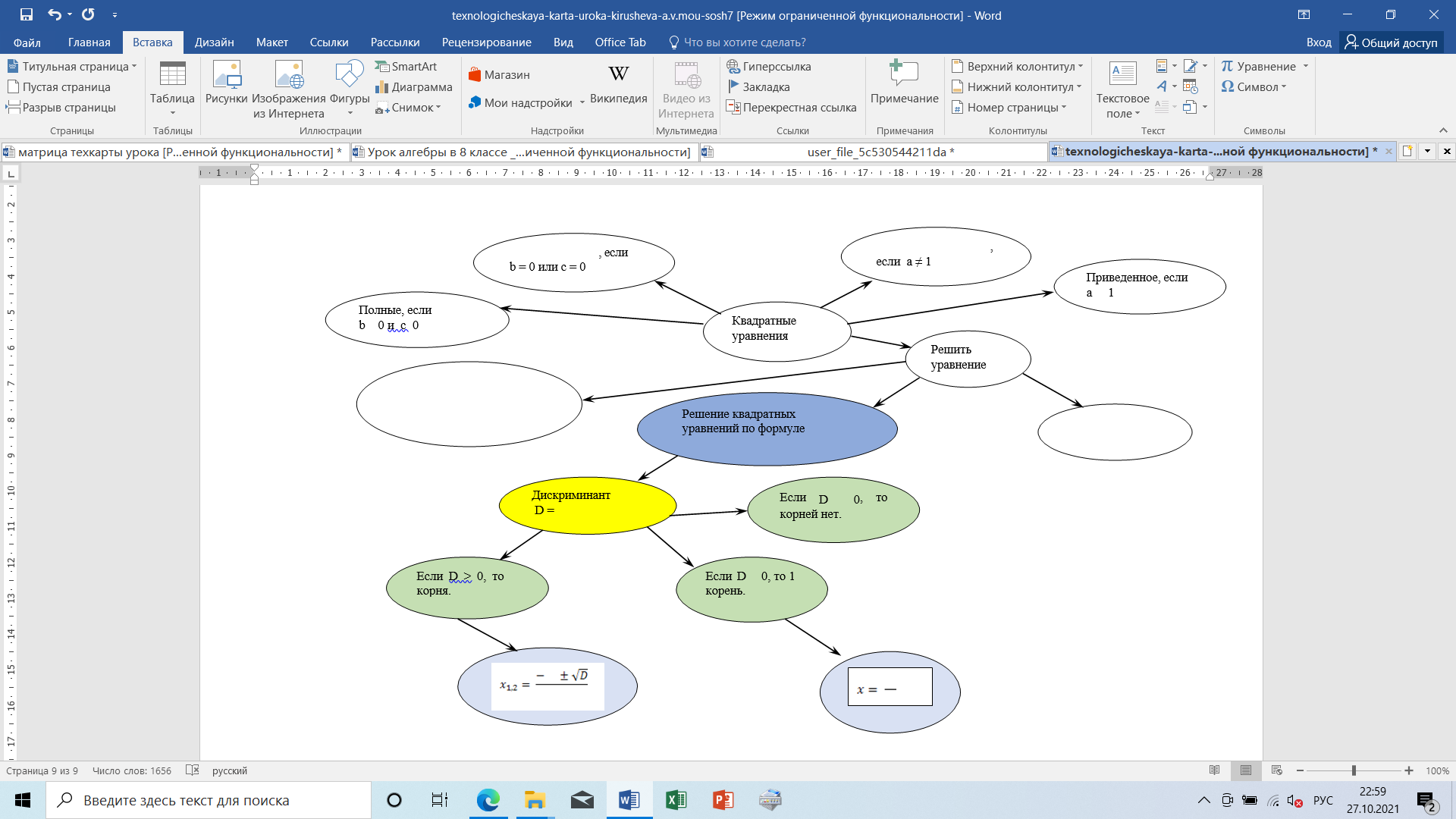
Этапы урока

Деятельность учителя

Деятельность учащихся

Формируемые УУД

Мотивация

1.Приветствиует обучающихся.

- Добрый день! Рада вас видеть!

«Приобретать знания - это храбрость. Приумножать знания - это мудрость. А умело применять - великое искусство.»

2. Проверяет подготовленность к учебному занятию, организация внимания детей

1.Приветствуют учителя

2.Оценивают готовность рабочего места

Личностные: эмоциональны настрой на урок

Регулятивные: самоконтроль

Актуализация

Опрос по ранее пройденному материалу:

- Что такое квадратное уравнение?

- Какие виды квадратных уравнений вы знаете?

- Какие способы решения квадратных уравнений вам известны?

Организует опрос обучающихся приемом «Работа с таблицей»

- Давайте проверим с помощью теста, на сколько хорошо вы умеете определять

виды квадратных уравнений.

Даны уравнения – напротив каждой колонки выставите плюс, если оно принадлежит

к данному виду

Организует проверку домашнего задания

- Ребята, дома вы решали квадратные уравнения.

1. х² + 3х = 0

2. х² + 7 = 0

3. х² - 4 = 0

4. х² + 8х + 16 = 0

5. х² + 8х + 9 = 0

6. 3 х² - 4х + 1 = 0

Отвечают на вопросы, работают с таблицей, проверяют выполненные задания

Личностные: мобилизация внимания, уважение к окружающим

Регулятивные: саморегуляция

Коммуникативные: планирование учебного сотрудничества с учителем, сверстниками

Выявление места и причины затруднения

Организует диалог с целью выяснения причин возникших затруднений при решении уравнений в домашнем задании

- Какие способы использовали? (решение неполных квадратных уравнений различного вида, способ разложение на множители методом выделения полного квадрата двучлена, метод группировки)

- Какое уравнение вызывало затруднение?

- Почему?

Фиксируют возникшие затруднения

- При решении 6-го уравнения трудно выделить полный квадрат, сложно применить способ группировки.

Регулятивные: постановка цели учебной деятельности, выбор способа и средств ее реализации; самоконтроль знаний

Познавательные: выбор наиболее эффективных способов решения задач в зависимости от конкретных условий, извлечение необходимой информации из учебника, постановка и формулирование проблемы;

Коммуникативные: планирование учебного сотрудничества с учителем, одноклассниками; умение с достаточной полнотой выражать мысли в соответствии с задачами и условиями коммуникации

Планирование

-Решать полные квадратные уравнения рассмотренными нами методами сложно и долго, или не всегда получаем точный результат

-Есть необходимость найти другой способ решения? (Да).

-Тогда давайте определимся с темой урока.

Какой главный вопрос поставим?

- Какова цель нашего урока?

Формулируют тему урока

- Решение полных квадратных уравнений

Определяют цель урока

- Получить новый способ решения полных квадратных уравнений. Употреблять данные знания на практике.

Реализация плана

1) Предлагает выполнить задание

• Формулу для решения квадратного уравнения

a x² + b x + c = 0

можно получить так:

1. перенесите c в правую часть

a x² + b x = - c

1. умножьте уравнение на 4a

(2a x)² + 4a b x = - 4a c

1. добавьте b² к обоим частям

2. (2a x)² + 4a b x + b² = b² - 4a c

3. в левой части выделите полный квадрат

4. (2a x + b)² = b² - 4a c

5. извлеките квадратный корень

6. 2a x + b = ± √b² - 4a c

7. перенесите b в правую часть

8. 2a x = - b ± √b² - 4a c

9. разделите уравнение на 2a

Обозначьте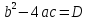 

D называют дискриминантом квадратного уравнения

• Выясните, сколько корней может иметь квадратное уравнение в зависимости от знака дискриминанта и составьте кластер, используя ключевые слова «квадратные уравнения»

2) Организует систематизацию знаний при заполнении алгоритма решения квадратного уравнения.

3) Оформляет решение уравнения

3 х² - 4х + 1 = 0 на доске.

4) Предлагает выполнить решение уравнений: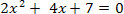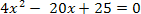

Ученики выполняют задание

1.Работают с текстом учебника, заполняют кластер

2.Делают выводы

3.Определяют, какая цель достигнута, что необходимо выяснить по данной теме

Записывают алгоритм на карточку. Решают уравнение 3 х² - 4х + 1 = 0 по алгоритму.

Выполняют решение на доске по желанию.

Познавательные: применяют знания при выводе формулы квадратных уравнений

Коммуникативные: Строят рассуждения при работе с текстом

Регулятивные: организация своей учебной деятельности.

Личностные: мотивация учения.

Физкультминутка

Ребята! Мы сейчас проведем физкультминутку, мы хорошо с вами поработали – пришло время отдохнуть.

Коль писать мешает нос,

Значит, это сколиоз

Вас сгибает над тетрадкой,

Позвоночник не в порядке.

Мы ему сейчас поможем:

Руки за голову сложим,

Повороты влево – вправо,

И наклоны влево – вправо,

Ручки к солнцу потянулись,

Мы назад ещё прогнулись,

Повращаем мы плечами,

Чтоб они не подкачали.

Улыбнулись всем, кто рядом.

Вот! Уже другой порядок!

А теперь повыше нос:

Нам не страшен сколиоз.

Сядем ровно, ручки – в руки,

Продолжаем путь к науке!

Ученики повторяют действия за учителем

Первичное закрепление

Организует первичное закрепление с помощью приема «Зигзаг»: Работа в группах по 4 человека:

Первые номера – первый пример карточки.

Вторые номера – второй пример карточки.

Третьи номера – третий пример карточки.

Четвертые номера – четвертый пример карточки.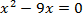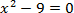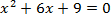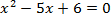

Работают в 4 –ках, решают уравнения по принципу

«Зигзаг», проверяют правильность решения по образцу. Результат выставляют в «Лист самоконтроля».

Познавательные: применяют знания при решении квадратных уравнений Регулятивные:

организация своей учебной деятельности.

Самостоятельная работа с самопроверкой по эталону

Предлагает выполнить самостоятельную работу. Решив задания 1 варианта, ребята отгадают фамилию знаменитого французского ученого, который впервые установил зависимость между корнями и коэффициентами квадратного уравнения (Виета)

2 варианта - английского математика который ввёл термин "дискриминант» (Джозеф)

Организует и контролирует процесс решения, взаимопроверку и самооценку.

Самостоятельно работают над заданиями.

Обучающиеся осуществляют взаимопроверку, оценивают работу, озвучивают фамилии ученых.

Регулятивные:

оценивание собственной деятельности на уроке.

Личностные:

чувство собственного достоинства.

Включение в систему знаний и повторение

Предлагает выполнить работу по учебнику № 656 (5,7,9)

№ 670 (1) (для сильных учащихся

Решают у доски

Личностные: объясняют сами себе «что я могу»

Регулятивные: контроль, коррекция, выделение и осознание того, что уже усвоено и что еще подлежит усвоению, осознание качества и уровня усвоения

Познавательные: структурирование знаний, выбор наиболее эффективных способов решения задач

Коммуникативные: уметь слушать и понимать речь, умение с достаточной полнотой и точностью выражать свои мысли.

Рефлексия

Предлагает вопросы

Вернемся к началу нашего урока.

- Верно ли, что приобретать знания – это храбрость?

- На каком этапе урока это проявлялось?

- Приумножать знания – это мудрость?

- А умело применять знания – это здорово?

1.Какую ставили цель?

Удалось решить поставленную цель?

Где можно применить новые знания?

Какой вид работы понравился?

Отвечают на вопросы

Личностные: самооценка, адекватное понимание успеха или неуспеха в учебной деятельности;

Регулятивные:контроль и оценка процесса и результатов деятельности;

Познавательные:рефлексия способов и условий действия

Домашнее

задание

Информирует о домашнем задании

1) П.20 учебника.

Выучить формулу дискриминанта, правило о количестве корней квадратного уравнения, формулу корней квадратного уравнения.

2) № 658(1,3), 660(1,3), 671(1)

3) Оформить красочно решение исторической задачи (по желанию):

Обезьянок резвых стая

Всласть поевши, развлекалась,

Их в квадрате часть восьмая

На поляне забавлялась.

А 12 по лианам… Стали прыгать, повисая. Сколько было обезьянок,

Ты скажи мне, в этой стае?

Обучающиеся записывают домашнее задание в дневник, задают вопросы учителю.

Прощаются с учителем.

Личностные: самоопределение

Регулятивные: саморегуляция, осознание качества и уровня усвоения знаний, оценка результатов работы;

Познавательные: добывать новые знания из различных источников и разными способами; самостоятельно предполагать, какая информация нужна для решения предметной задачи, сопоставлять и отбирать информацию из различных источников

Коммуникативные:инициатива в выборе задачи, поиск и сбор информации

Ф.И.

полное

неполное

приведенное

неприведенное

Общий балл

1. х² + 8х +3 = 0

+

+

2. 6х² + 9 = 0

+

+

3. х² – 3х = 0

+

+

4. –х² + 2х +4 = 0

+

+

5. 3х + 6х² + 7 =0

+

+

1

2

3

4

^Х1 ^{= 0, Х}2 ^{= 9.}

^Х1 ^{= - 3, Х}2 ^{= 3.}

Х = - 3.

^Х1 ^{= 2, Х}2 ^{= 3.}

9

3; 6;-6

2; -1/3

25

-3; -2

И

В

Т

Е

А

144

1; 5

16

-4; 6

0,25; 1

4; -8; 6

Ж

З

О

Е

Ф

Д