Урок по алгебры 8 класс
Тема: «Решение задач с помощью квадратных уравнений»
Тип урока: изучение нового материала.
Цели урока: научить решать текстовые задачи с помощью квадратных уравнений, создание учебно-методических условий, способствующих достижению обучающимися следующих результатов:
- предметных:
осмысление ранее изученных понятий «выражение переменных из формул», «решение квадратных уравнений», умения составлять уравнения по тексту задачи, овладение навыками составления и решения квадратных уравнений.
-метапредметных:
решение практических задач; умение самостоятельно выполнять работу;
способность вступать в речевое общение, участвовать в диалогах;
формировать умения оценивать свои учебные достижения, свое эмоциональное состояние.
- личностных:
проявление воли и настойчивости для достижения конечных результатов;
умение выдвигать гипотезы, отыскивать решения и рассуждать логично;
формирование навыков самостоятельной работы и самооценки знаний.
Используемые формы работы:
- индивидуальная;
- групповая;
- фронтальная.
Методы работы:
1. методы организации учебно-познавательной деятельности: словесный, наглядный, практический, самостоятельная работа, работа под руководством.
2. методы контроля и самоконтроля: устный опрос; фронтальный опрос; письменный контроль; взаимный контроль; самоконтроль.
План урока:
1. Организационный момент.
2. Проверка домашнего задания.
3. Актуализация опорных знаний.
4. Работа по изучению нового материала.
5. Закрепление пройденного материала.
6. Самооценка.
7. Подведение итогов урока.
8. Задание на дом.
ХОД УРОКА.
Организационный момент.
Класс «разбит» на пары : «сильный + слабый» ученик.
Цель: настроить учащихся на урок.
| Деятельность учителя | Деятельность учеников |
| Приветствие. Мы сегодня будем заниматься решением задач с помощью составления квадратных уравнений.
| Приветствие. Записывают в тетрадях число, «классная работа», тему урока. |
2. Проверка домашней работы.
Цель: коррекция ошибок.
| Деятельность учителя | Деятельность учеников |
| На доске ответы к номерам из домашней работы. Учитель контролирует процесс, отвечает на вопросы по домашнему заданию. | Ученики самостоятельно проверяют, отмечая в тетрадях верные/неверные ответы, задают вопросы учителю. По окончанию проверки домашнего задания ученики самостоятельно выставляют оценки в тетрадях. |
3. Актуализация опорных знаний.
Цель: повторить основные понятия, формулы.
| Деятельность учителя | Деятельность учеников |
| Фронтальный опрос. Вопросы учащимся: Какое уравнение называется квадратным?
Какие виды квадратных уравнений вы знаете? Чем они отличаются?
Что такое корень уравнения?
От чего зависит количество корней квадратного уравнения? | Отвечают на поставленные вопросы: Квадратное уравнение – уравнение вида ах2+вх+с=0, где а, в, с – числа, причем а ≠0. ≠0. Полные, приведенные (старший коэффициент а=1), неполные (если хотя бы один из коэффициентов (в,с) равен 0). Корень уравнения – значение переменной, при котором квадратный трехчлен обращается в нуль. Количество корней уравнения зависит от его дискриминанта. |
Каждому ученику перед началом урока на парту был выдан тест, дифференцируемый по уровню сложности.
Учащиеся приступают к выполнению теста:
А1. Определите количество корней квадратного уравнения:
| Вариант 1 | Х2-4х+3=0 | 1) 0 2) 1 3) 2 4) 3 |
| Вариант2 | Х2-2х-2=0 | 1) 0 2) 1 3) 2 4) 3 |
| Вариант3 | 36Х2-12х+1=0 | 1) 0 2) 1 3) 2 4) 3 |
| Вариант4 | 2Х2-44х-46=0 | 1) 0 2) 1 3) 2 4) 3 |
А2. Решите уравнение:
| Вариант 1 | Х2+5х=0 | 1) 0;5 2) 1;5 3) 0;-5 4) 1;-5 |
| Вариант2 | Х2-49=0 | 1) 0;49 2)-49;49 3) -7;7 4)нет корней |
| Вариант3 | -2Х2+14х=0 | 1)7;0 2)-7;0 3)1;7 4)-1;7 |
| Вариант4 | 4Х2+ 68=0 | 1) 17/4 2) -17/4 3)± 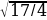 4) нет корней 4) нет корней |
А3.Найдите наибольший корень уравнения:
| Вариант 1 | 2Х2-7х+5=0 | 1) 1 2) 2,5 3) 3 4) 3,5 |
| Вариант2 | 3Х2-2х-1=0 | 1) 1 2)-1/3 3) -1 4) 3 |
| Вариант3 | 8Х2-14х+6=0 | 1)1 2)-3/4 3)3/4 4) 3 |
| Вариант4 | 4Х2-18х +14=0 | 1) 0 2) 1 3)3,5 4) 2 |
Проверка происходит с экрана, ученики обмениваются тетрадями с соседом по парте.
|
| А1 | А2 | А3 |
| Вариант 1 | 3 | 3 | 2 |
| Вариант2 | 3 | 3 | 1 |
| Вариант3 | 2 | 1 | 1 |
| Вариант4 | 3 | 4 | 3 |
4. Работа по изучению нового материала.
Цель: показать расширение аппарата уравнений для решения текстовых задач.
| Деятельность учителя | Деятельность учеников |
| С помощью квадратных уравнений решаются многие задачи в математике, физике, технике. Сколько решений может иметь задача, решенная с помощью линейного уравнения? Сколько же решений может иметь задача, решенная с помощью квадратного уравнения?
На экран выводится пример первой задачи с решением. Происходит коллективная работа класса под руководством учителя: обсуждение алгоритма решения задачи, что известно, что обозначим за «х», повторение теоремы Пифагора, анализ составленного уравнения, обсуждение полученных результатов. |
При решении задач с помощью линейных уравнений или систем (рассмотренных ранее) могло быть два случая: одно решение или ни одного
Обсуждают решение предложенной задачи, отвечают на поставленные учителем вопросы. На экране: Задача 1. Найдите катеты прямоугольного треугольника, если известно, что один из них на 4 см меньше другого, а гипотенуза равна 20 см. Решение: Пусть меньший катет равен х см, тогда больший катет равен (х+4) см. По теореме Пифагора квадрат гипотенузы равен сумме квадратов катетов, т.е. х2+(х+4)2=202. Упростим это уравнение: х2+х2+8х+16=400, 2х2+8х-384=0, х2+4х-192=0. Решив полученное квадратное уравнение, найдем, что х1=-16, х2 = 12. По смыслу задачи значение х должно быть положительным числом. Этому условию удовлетворяет только второй корень, т.е. число 12 – меньший катет. Тогда больший катет будет 16 см. Ответ: 12 см, 16 см.
|
5. Закрепление пройденного материала.
№ 559. Произведение двух натуральных чисел, одно из которых на 6 больше другого, равно 187. Найдите эти числа.
| Деятельность учителя | Деятельность учеников |
|
Какие числа называются натуральными? Какое самое маленькое натуральное число? Известно ли нам хотя бы одно из чисел? Что мы обозначаем за «х»? | «Сильный» ученик решает у доски с подробным объяснением, остальные - в тетрадях. Натуральные – числа, которые используются для счета предметов. Самое маленькое натуральное число - 1. Нет.
- Наименьшее. Решение: Пусть 1 натуральное число – х, тогда 2 натуральное число – (х+6). Произведение этих чисел равно 187. Составим и решим уравнение: х (х+6) = 187 х2 + 6х -187=0 D =36-4×1×(-187)=784 › 0 → уравнение имеет 2 действительных различных корня х1=-17 – не удовлетворяет условию задачи, х2=11 – 1 число, тогда 2 число : 17. Ответ: 11; 17. |
№ 560. Найдите периметр прямоугольника, длина которого на 4 см больше ширины, а площадь равна 60 см2.
| Деятельность учителя | Деятельность учеников |
| Контролирует процесс решения задачи, отвечает на вопросы. | «Сильный» ученик решает у доски с подробным объяснением, остальные - в тетрадях. Решение: Пусть ширина прямоугольника – х см, тогда длина (х+4) см. По условию задачи площадь прямоугольника равна 60 см2. Составим и решим уравнение: Х (х+4) = 60 х2+4х-60=0 D1= 22-1×(-60) = 4+60= 64. Х1= -10 – не удовлетворяет условию задачи, х2=6 – ширина прямоугольника, тогда длина 10 см. Периметр Р=2(а+в) , Р= 2( 6+10)= 32 (см). Ответ: 32 см. |
№ 562. Периметр прямоугольника равен 62 м. Найдите его стороны, если площадь прямоугольника равна 210 м2.
| Деятельность учителя | Деятельность учеников |
| Контролирует процесс решения задачи, отвечает на вопросы. | Один ученик решает у доски с подробным объяснением, остальные - в тетрадях. Решение: По условию периметр прямоугольника равен 62 м, значит Р= 2(а+в)=62, тогда полупериметр равен Р/2= а+в=31 (м). Пусть одна сторона прямоугольника равна х м, тогда вторая сторона (31-х) м. По условию задачи площадь прямоугольника 210 м2. Составим и решим уравнение: х ( 31-х)= 210 х2 – 31х + 210=0 D= 121 Х1= 10 х2=21 . Ответ: 10м; 21 м. |
№ 563. Найдите катеты прямоугольного треугольника, если известно, что их сумма равна 23 см, а площадь данного треугольника равна 60 м2.
| Деятельность учителя | Деятельность учеников |
| Контролирует процесс решения задач, отвечает на вопросы. | Работа в парах: «сильный» ученик помогает «слабому» с последующей проверкой – отвечает «слабый» ученик. Решение: Пусть один катет прямоугольного треугольника равна х м, тогда второй катет (23-х) м. По условию задачи площадь треугольника 60 м2. Составим и решим уравнение: ½ х ( 23-х)= 60 D= 49 Х1= 8 х2=15 . Ответ: 8 см; 15 см. |
6. Самооценка.
| Деятельность учителя | Деятельность учеников |
| Учитель предлагает оценить свою работу на уроке учащимся и поставить оценки в выданных каждому бланках | Работают с индивидуальными бланками Отвечают на поставленный в начале урока вопрос. |
Индивидуальные бланки:
|
| Вид работы | Оценка |
| 1 | Выполнил тест |
|
| 2 | Правильно оформил и решил задачу № 563 |
|
| 3 | Правильно оформил и решил задачу № 568 |
|
| 4 | Активно работал на уроке |
|
7. Подведение итогов.
| Деятельность учителя | Деятельность учеников |
| Самоанализ учащихся по вопросам: Какая цель была у нас на уроке? Хорошо ли мы повторили и закрепили решение квадратных уравнений и задач? Как вы думаете, пригодятся ли вам знания, которые мы сегодня получили? Появилось ли у вас желание больше узнать о задачах? С каким настроение вы находились на уроке? Отметки получают те ученики, кто отвечал у доски и активно работал с места. Учитель отвечает на вопросы, комментирует оценки за урок. Спасибо за активную работу! |
Научиться решать задачи с помощью квадратных уравнений. Да
Да
Да
С хорошим.
|
8. Задание на дом.
Учитель дает рекомендации по выполнению домашнего задания: прочитать П. 23, решить№ 561, 564, 566.
6







 ≠0.
≠0.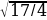 4) нет корней
4) нет корней









