Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа №2 г. Нижний Ломов
«Математика в искусстве»

Выполнили:
ученицы8 «Б» класса
МБОУ СОШ №2 г.Нижний Ломов,
Балахонова Алёна,Вострокнутова Анастасия
Руководитель:
Буренкова Галина Николаевна,
учитель математики МБОУ
СОШ №2 г. Нижний Ломов
г.Нижний Ломов,2020
Содержание:
Введение……………………………………………………………………………………3
Цели и задачи………………………………………….…………………………………...3
Выдающиеся люди истории математического искусства…………………………………..…………………………………………….…3
Общие темы в математическом искусстве и их примеры………………..…………………………………………………………………..4
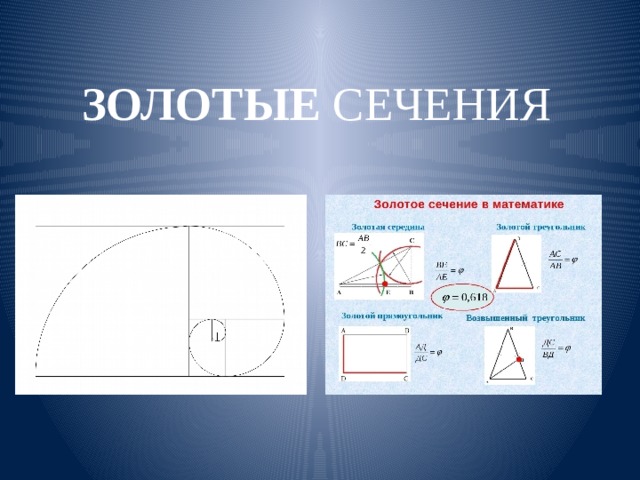
Золотые сечения……………………………………………………………………..…….4
В математике……………………….…………………………………………..………….4
В искусстве…………………………………………………………………………..…….4
Значение золотого сечения……………………………………………………………….4
Примеры золотого сечения…………………………………………………………...…..4
Исследование на картинах художников Пензенской области………………………….5
Вывод……………………………………………………………………………………….6
«Рано или поздно всякая правильная математическая идея находит применение в том или ином деле»
А.Н. Крылов
«Математика есть прообраз красоты мира»
В.Гейзенберг
Наука и искусство- два основных начала в человеческой культуре, две дополняющие друг друга формы высшей творческой деятельности человека: даже в самой сердцевине науки есть капля искусства, а каждое искусство несет в себе частицу научной мудрости.Исторически математика играла важную роль в изобразительном искусстве, в частности при изображении перспективы.
Согласно современным взглядам, математика и искусство- весьма отдаленные друг от друга дисциплины, первая- аналитическая, вторая- эмоциональная. Математика не играет очевидной роли в работах современных художников, во многих отсутствует та же перспектива в принципе, но есть и такие художники, у которых математика находится в центре внимания.
Цель нашей работы:
Исследование связи математики и различных видов искусства, формирование интереса к математике, к ее свойствам, законам.
Для достижения заданной цели необходимо решить следующие задачи:
1) Изучить методическую, научно-популярную и тематическую литературу.
2) Используя литературу выбрать комплекс наиболее интересных и увлекательных примеров связи математики и искусства.
М. К. Эшер.В некотором роде этот голландский художник является отцом математического искусства. Математические идеи играют центральную роль в большинстве его картин за исключением лишь ранних работ. Большинство идей, часто используемых современными математическими художниками, были использованы Эшером, и его работы часто являются источником вдохновения для современных авторов.
Сальвадор Дали.Дали в некоторых своих произведениях тоже использовал математические идеи. В данной картине «Распятие», например, изображен гиперкуб. А на картине «LaVisagedelaGuerre» последовательность уменьшающихся лиц.
Леонардо Да Винчи.Известен своими достижениями в качестве изобретателя и художника. В его записных книгах содержатся первые из известных примеров анаморфного искусства, использующего искаженные сетки перспективы. Его наклонные анаморфные изображения представляют объекты, которые должны рассматриваться по углом, чтобы они выглядели неискаженными.
Пит Мондриан.Мондриан призывал к «денатурализации» искусства, к отказу от естественных форм и переходу к чистой абстракции. Начиная с 1913 года, картины Мондриана развивалисьв сторону абстрактных матриц,состоящих из чёрных горизонтальных и вертикальных линий. Постепенно расположение линий на холсте упорядочилось до такой степени, что они стали представлять собой правильные решётки с ячейками. Ячейки закрашивались основными цветами, то есть красным, синим и жёлтым. Таким образом, структуру картины образовывали дихотомии цвет — не-цвет, вертикаль — горизонталь, большая поверхность — малая поверхность, единение которых должно было символизировать равновесие сил в гармонии мироздания. Несмотря на предельную ограниченность визуальных средств, творчество Мондриана оказало большое влияние на современников и породило новые направления в живописи и графике.
Общие темы в математическом искусстве:
Многогранники
Тесселляции
Невозможные фигуры
Лента Мебиуса
Искаженные и необычные перспективы
Фракталы
Золотое сечение. Золотое сечение - это пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему:
a : b = b : c или с : b = b : а.
Под «правилом золотого сечения» в архитектуре и искусстве обычно понимаются асимметричные композиции, не обязательно содержащие золотое сечение математически.
Многие утверждают, что объекты, содержащие в себе «золотое сечение», воспринимаются людьми как наиболее гармоничные.
Значение.Есть основание считать, что значимость золотого сечения в искусстве преувеличена и основывается на ошибочных расчётах. Некоторые из таких утверждений:
Пропорции пирамиды Хеопса, храмов, барельефов, предметов быта и украшений из гробницы Тутанхамона якобы свидетельствуют, что египетские мастера пользовались соотношениями золотого сечения при их создании.
Согласно Ле Корбюзье, в рельефе из храма фараона Сети I в Абидосе и в рельефе, изображающем фараона Рамзеса, пропорции фигур соответствуют золотому сечению. В фасаде древнегреческого храма Парфенона также присутствуют золотые пропорции. В циркуле из древнеримского города Помпеи (музей в Неаполе) также заложены пропорции золотого деления, и т. д. и т. п.
Результаты исследования золотого сечения в музыке впервые изложены в докладе Эмилия Розенова (1903) и позднее развиты в его статье «Закон золотого сечения в поэзии и музыке» (1925). Розенов показал действие данной пропорции в музыкальных формах эпохи Барокко и классицизма на примере произведений Баха,Моцарта, Бетховена.

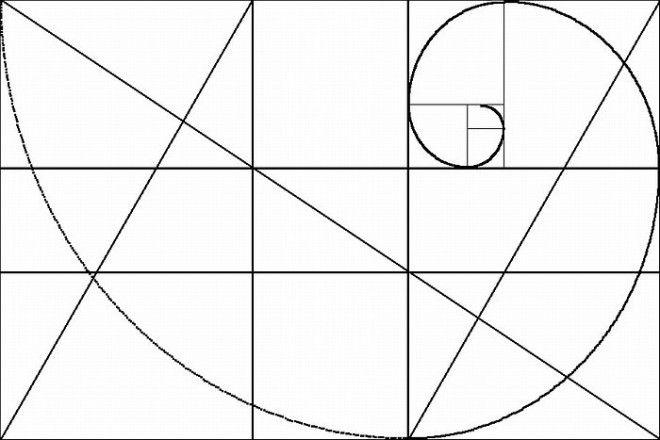 Одним из примеров «золотого сечения» является творчество Леонардо да Винчи. Он посвятилмного времени изучению особенностей золотого сечения, скорее всего именно ему принадлежит и сам термин. Его рисунки стереометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения сторон в золотом делении.
Одним из примеров «золотого сечения» является творчество Леонардо да Винчи. Он посвятилмного времени изучению особенностей золотого сечения, скорее всего именно ему принадлежит и сам термин. Его рисунки стереометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения сторон в золотом делении.
Исследование на примере картин художников Пензенской области
Тема нашего проекта очень увлекла нас, поэтому мы решили провести свое исследование. Мы подобрали несколько картин художников нашей области и постарались определить, каким математическим законам они подчиняются. Вот что у нас получилось:
На этой картине Алексея Головченко мы можем увидеть пример золотого сечения.

А на этой картине Анны Козловой мы видим пример перспективы, которая делает произведение живописи естественным.

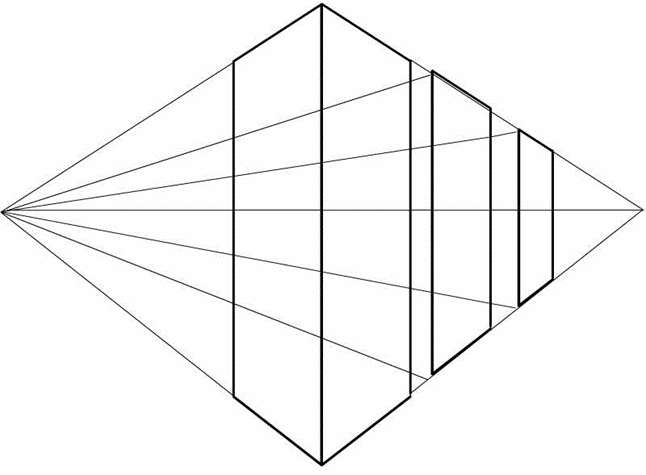
Анатомия это тоже расчеты и схемы. При изображении человека, нужно соблюдать определенные пропорции. На картине Владимира Мухина мы можем это увидеть.


Вывод: в результате нашего исследования, мы выяснили, что математика тесно связана с искусством, а именно с живописью. Множество знаменитых художников были успешными математиками. Так же мы выяснили, что в большинстве картин можно разглядеть те, или иные законы математики, так картины выглядят более гармоничными и приближенными к реальности.
Источники информации:







 Одним из примеров «золотого сечения» является творчество Леонардо да Винчи. Он посвятилмного времени изучению особенностей золотого сечения, скорее всего именно ему принадлежит и сам термин. Его рисунки стереометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения сторон в золотом делении.
Одним из примеров «золотого сечения» является творчество Леонардо да Винчи. Он посвятилмного времени изучению особенностей золотого сечения, скорее всего именно ему принадлежит и сам термин. Его рисунки стереометрического тела, образованного правильными пятиугольниками, доказывают, что каждый из полученных при сечении прямоугольников дает соотношения сторон в золотом делении.