Просмотр содержимого документа
«Симметрия в алгебре»

ГБОУ СПО "Трубчевский политехнический техникум"
Низикова Зоя Константиновна
Преподаватель математики

Симметрия
в
Алгебре
Симметрические многочлены

“ Симметрия”
Симметрия (от греч. symmetria — соразмерность), Пропорциональность, соразмерность в расположении частей целого в пространстве, полное соответствие (по расположению, величине) одной половины целого другой половине.

Симметрия в живой природе, неживой природе, архитектуре и символизме

Известный немецкий математик нашего столетия Герман Вейль дал определение симметрии таким образом:
“ Симметрия является той идеей, с помощью которой человек веками пытается объяснить и создать порядок, красоту и совершенство”.
Герман Клаус Гуго Вейль — немецкий математик и физик-теоретик. Лауреат премии Лобачевского (1927 год).

Примеры числовых симметрий
- В записи чисел: 101, 303, 54045, 245606542
42 + 35 = 53 + 24 41 – 32 = 23 – 14
53 + 24 = 42 + 35 52 – 43 = 34 – 25
53 + 46 = 64 + 35 63 – 54 = 45 – 36
75 + 68 = 86 + 57 74 – 65 = 56 – 47

Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму.
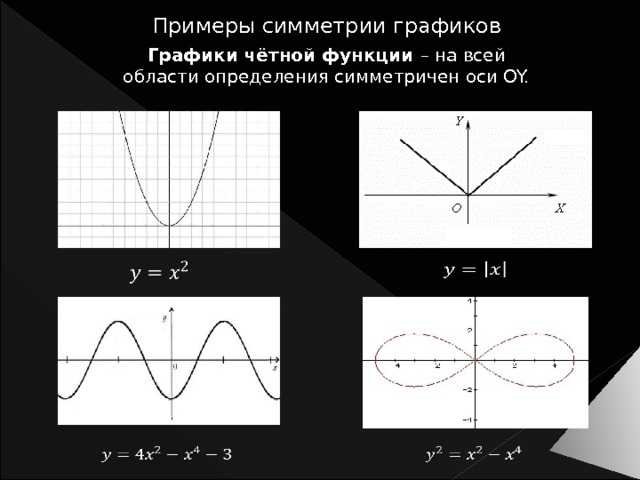
Примеры симметрии графиков
Графики чётной функции – на всей области определения симметричен оси OY.

Примеры симметрии графиков
Графики нечётной функции – симметричен относительно начала координат точки 0.

Симметрические выражения
Симметричные выражения с двумя переменными:
Если заменить то получим
Значения не меняются при взаимной замене переменных

Симметрические выражения применяются при решении задач на применение теоремы Виета
Например:
Найти:
- Квадрат суммы корней
- Квадрат разности корней
- Сумму квадратов корней
- Сумму кубов корней
Симметрические выражения применяются при решении уравнений высших степеней вида:

Элементарные симметрические многочлены
Симметрические суммы

Выражение степенных сумм через элементарные симметрические многочлены
Выражение степенных сумм через и

Алгоритм решения
Решение симметричных систем управлений
- Перейти к новым неизвестным
- Найти значение первоначальных неизвестных и

Связь
Между квадратным уравнением
Системой уравнений
Если - корни уравнения, то система имеет два решения
И других решений не имеет
Обратно: Если – решение системы, то числа a и b – корни квадратного управления.

Пример решения системы симметрических уравнений
Положим:
Получим:
Далее:
Решение:

Симметрические многочлены применяются при решении:
- Систем симметрических уравнений
- Неравенств
- Возвратных уравнений
- Освобождение от иррациональности в знаменателях
- Разложение на множители
- Доказательств тождеств и уравнений алгебраических выражений
Преимущества:
- Понижают степень
- Упрощают вычисления

Спасибо за внимание!


































