Синтез логических выражений

Тема: "Синтез логических выражений".

Цель работы: 

Получение практических навыков синтеза логических выражений из таблиц истинности.

Количество часов на выполнение работы

Продолжительность выполнения данной практической работы составляет 2 академических часа.

Оборудование

• тетрадь;

• ручка (карандаш);

• калькулятор.

Краткие теоретические сведения

Логика - это наука о законах и формах мышления, направленная на познание объективного мира. Слово логика обозначает совокупность правил, которым подчиняется процесс мышления или обозначает науку о правилах рассуждения и тех формах, в которых оно осуществляется.

Алгебра логики - раздел математики. Она оперирует логическими высказываниями.

Логическое высказывание - любое предложение в повествовательной форме, о котором можно однозначно сказать, истинно оно или ложно.

Примеры логических высказываний:

"Москва - столица России" (высказывание истинно).

"После зимы наступает осень" (высказывание ложно).

Простое высказывание - логическое высказывание, состоящее из одного утверждения.

Сложное высказывание - логическое высказывание, состоящее из нескольких утверждения, объединенных с помощью "связок": союзов "и", "или (либо)", частицы "не", связки "если, то" и др.

Логические операции - "связки": союзы и частицы естественного языка, образующие из простых высказываний сложные, представленные в формальном виде.

Логическое выражение - простое или сложное логическое высказывание, представленное в формальном виде.

Законы алгебры логики - законы, позволяющие преобразовывать логические выражения.

Логическая переменная - переменная, которая может принимать значение 1 (истина) или 0 (ложь).

Связки "НЕ", "И", "ИЛИ", "ЕСЛИ, ТО" - логические операции

Существуют разные варианты обозначения истинности и ложности логических переменных:

Рисунок 1 – Обозначения истинности и ложности логических переменных

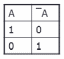
Рисунок 2 – Инверсия

Рисунок 3 – Конъюнкция

Рисунок 4 – Дизъюнкция

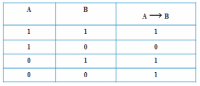
Рисунок 5 – Импликация

Рисунок 6 – Эквивалентность

Логические выражения можно преобразовывать в соответствии с законами алгебры логики:

Законы рефлексивности:

• a ∨ a = a

• a ∧ a = a

Законы коммутативности:

• a ∨ b = b ∨ a

• a ∧ b = b ∧ a

Законы ассоциативности:

• (a ∧ b) ∧ c = a ∧ (b ∧ c)

• (a ∨ b) ∨ c = a ∨ (b ∨ c)

Законы дистрибутивности:

• a ∧ (b ∨ c) = a ∧ b ∨ a ∧ c

• a ∨ b ∧ c = (a ∨ b) ∧ (a ∨ c)

Закон отрицания отрицания:

• ¬ (¬ a) = a

Законы де Моргана:

• ¬ (a ∧ b) = ¬ a ∨ ¬ b

• ¬ (a ∨ b) = ¬ a ∧ ¬ b

Законы поглощения:

• a ∨ a ∧ b = a

• a ∧ (a ∨ b) = a

Задания по практической работе

1. Упростить логическое выражение, используя законы алгебры логики и построить таблицу истинности: ¬ ( K ˄ L ˅ ¬ ( L ˅ M ) ) ~ M ˄ N ˅ M

2. Упростить логическое выражение, используя законы алгебры логики и построить таблицу истинности: ¬ ( K ˅ K ˄ M ~ ( L ˅ N ) ˄ ¬ ( N ˄ K ) )

3. Упростить логическое выражение, используя законы алгебры логики и построить таблицу истинности: ¬ ( K ˄ ( K → L ) ˅ ( K ˅ N ) ˄ ( M ˅ N ) )

4. Упростить логическое выражение, используя законы алгебры логики и построить таблицу истинности: N ˄ ¬ ( L ˄ N ) → ( ¬ ( N ˅ K ) ˅ K ˄ M )

5. Упростить логическое выражение, используя законы алгебры логики и построить таблицу истинности: ¬ ( K ˅ K ˄ M ~ ( L ˅ N ) ˄ ¬ ( N ˄ L ) )

Контрольные вопросы

1. Что такое логика и алгебра логики?

2. Что такое логическое высказывание? Какие они бывают?

3. Что такое логические операции и выражения? Какие они бывают?

4. По каким правилам выполняется упрощение логических операций?