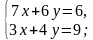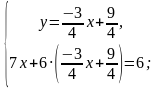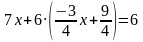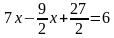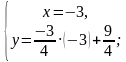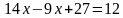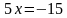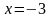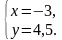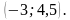Способ подстановки при решении систем линейных уравнений с двумя переменными.
Теперь рассматриваем алгебраический способ решения системы линейных уравнений с двумя переменными. Называется он способ подстановки. По названию вы уже, наверное, догадались, что мы будем что-то вместо чего-то подставлять. Составим сразу алгоритм, а затем на примерах разберём, как он работает.
При решении системы линейных уравнений с двумя переменными способом подстановки, необходимо:
в каком-нибудь из уравнений выразить одну переменную через другую;
в другое уравнение подставить вместо этой переменной полученное выражение;
решить получившееся уравнение с одной переменной;
подставить её значение в первое уравнение и найти значение второй переменной.
Прежде чем рассмотреть пример, определим форму записи решения систем уравнений. Системы можно решать в столбик, записывая систему под системой, а решение уравнения с одной переменной вынести из системы и записать справа. Можно записывать решение систем в строчку через знак равносильности 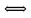 . В этом случае уравнение с одной переменной решается ниже, пропуская немного места для завершения решения системы. На примерах покажем оба способа записи.
. В этом случае уравнение с одной переменной решается ниже, пропуская немного места для завершения решения системы. На примерах покажем оба способа записи.
Например, решить систему 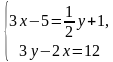 способом подстановки.
способом подстановки.
Внимательно рассматриваем первое и второе уравнение и прогнозируем для себя, из какого уравнения какую переменную легче выразить. В нашем примере легче выразить переменную у через переменную х в первом уравнении. Для этого:
умножим обе части на 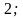
перенесём 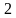 в другую часть с противоположным знаком (поменяем сразу местами левую и правую часть);
в другую часть с противоположным знаком (поменяем сразу местами левую и правую часть);
затем во второе уравнение вместо у подставляем 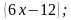
находим значение 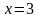 , решая второе уравнение;
, решая второе уравнение;
найденное значение 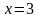 подставляем в первое уравнение;
подставляем в первое уравнение;
находим значение у;
полученные значения и являются решением системы и записываются в ответе в виде координат точки (не забываем, что на первом месте стоит х, а на втором у).
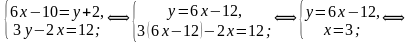
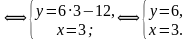
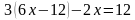
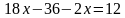
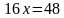
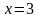
Ответ: 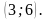
Приведём ещё один пример. Решить систему 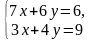 способом подстановки.
способом подстановки.
Выбираем уравнение, в котором будем выражать одну переменную через другую. Удобнее это сделать во втором уравнении, выражать будем у, т.к. у него коэффициент равен 4, а делить на 4 любое число просто.
Подставляем выраженную переменную в первое уравнение.
Решаем уравнение с одной переменной, находим значение х.
Подставляем это значение во второе уравнение и находим значение у.
Заметим, что в системе можно переставлять (для удобства) местами уравнения. В данном случае выражаем у из второго уравнения, а записываем на первом месте.
Ответ: 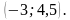
Используя способ подстановки, решить систему уравнений:
Решите систему уравнений способом подстановки. В ответе запишите значение выражения  , где
, где  – решение данной системы.
– решение данной системы.
Пусть  – решение системы уравнений. Найдите
– решение системы уравнений. Найдите 
Пусть  – решение системы уравнений. Найдите
– решение системы уравнений. Найдите 
Решить систему уравнений способом подстановки:
Укажите, сколько решений имеет система уравнений:
(*) Решите систему уравнений:
Решить систему уравнений с параметром:
3







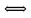 . В этом случае уравнение с одной переменной решается ниже, пропуская немного места для завершения решения системы. На примерах покажем оба способа записи.
. В этом случае уравнение с одной переменной решается ниже, пропуская немного места для завершения решения системы. На примерах покажем оба способа записи.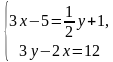 способом подстановки.
способом подстановки.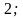
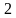 в другую часть с противоположным знаком (поменяем сразу местами левую и правую часть);
в другую часть с противоположным знаком (поменяем сразу местами левую и правую часть); 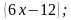
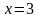 , решая второе уравнение;
, решая второе уравнение;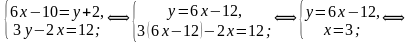
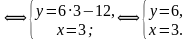
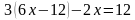
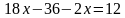
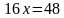
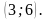
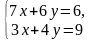 способом подстановки.
способом подстановки.