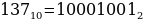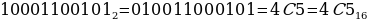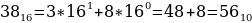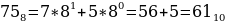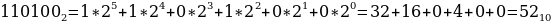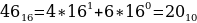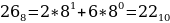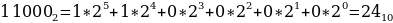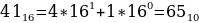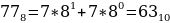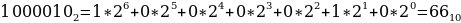Сравнение чисел в различных системах счисления.
Системы счисление:
Двоичная
Восьмеричная
Десятичная
Шестнадцатеричная
Двоичные числа – каждая цифра обозначает значение одного бита (0 или 1), старший бит всегда пишется слева, индекс обозначает основание системы счисления. Например, 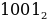 .
.
В восьмеричной системе счисления используется восемь знаков-цифр (от 0 до 7).
Десятичные числа – наиболее привычные для обычного человека в повседневной жизни (от 0 до 9). Обозначаются индексом 10. Например, 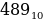 .
.
Шестнадцатеричная система счисления, так же как восьмеричная, широко используется в компьютерной науке из-за простоты перевода в нее двоичных чисел. В случае шестнадцатеричной записи числа получаются более компактными. В качестве алфавита шестнадцатеричной системы счисления используются цифры от 0 до 9 и шесть первых латинских букв – A, B, C, D, E, F.
Для того чтобы сравнить числа в различных системах счисления, необходимо выполнить перевод из различных систем счисления в десятичную.
Для перевода чисел в десятичную систему счисления выполняют развернутую запись исходного числа.
В двоичной системе счисления с увеличением значения количество разрядов растет очень быстро. Как определить, что значит двоичное число 10001001? Нам сложно понять, сколько это, мы привыкли мыслить в десятичной системе. Поэтому часто используется перевод двоичных чисел в десятичные.
В десятичной системе счисления любое число можно представить в форме суммы единиц, десяток, сотен и так далее. Например:
5476 = 5000 + 400 + 70 + 6
Можно пойти еще дальше и разложить число, используя основание системы счисления, возводимое в показатель степени, равный разряду цифры, уменьшенному на единицу:
5476 = 5 * 103 + 4 * 102 + 7 * 101 + 6 * 100
После равенства числа 5, 4, 7 и 6 – это набор цифр, из которых состоит число 5476. Все эти цифры умножаются на десять, возведенную в ту или иную степень. Десять – это основание десятичной системы счисления. Степень, в которую возводится десятка – это разряд цифры за минусом единицы. Так, например, 6 находится в первом разряде, поэтому она умножается на 10. Натуральное число в нулевой степени равно единице. Таким образом, мы умножаем 6 на 1.
Точно также производится разложение числа в двоичной системы счисления, кроме того, что основанием выступает двойка, а не десятка. Здесь до знака равенства число представлено в двоичной системе счисления, после "равно" запись идет в десятичной:
10001001 = 1 *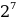 + 0 *
+ 0 *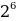 + 0 *
+ 0 *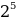 + 0 *
+ 0 * 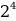 + 1 *
+ 1 * 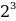 + 0 *
+ 0 * 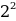 + 0 *
+ 0 * 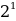 + 1 *
+ 1 * 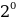
Результат вычислений дает десятичное число, количественно равное двоичному 10001001:
1*27 + 0*26 + 0*25 + 0*24 + 1*23 + 0*22 + 0*21 + 1*20 = 128 + 0 + 0 + 0 + 8 + 0 + 0 + 1 = 137
То есть число 10001001 по основанию 2 равно числу 137 по основанию 10:
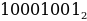 =
= 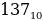
Для преобразования двоичного числа в восьмеричное надо разбить его на тройки цифр и заменить каждую тройку соответствующей ей одной цифрой из восьмеричной системы счисления. Разбивать двоичное число на тройки следует с конца, а вместо недостающих цифр в начале можно записать нули.
1011101 = 1 011 101 = 001 011 101 = 1 3 5 = 135
В примере число 1011101 в двоичной системе приводится к числу 135 в восьмеричной системе счисления.
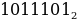 =
= 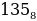
Как перевести восьмеричное число в десятичное? Здесь действует тот же алгоритм, как при преобразовании двоичного числа в десятичное. Однако в случае восьмеричного числа за основание степени берется десятичное число 8:
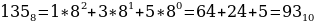
Перевод из шестнадцатеричной системы счисления в десятичную выполняется аналогично переводу из двоичной и восьмеричной. Только здесь в качестве основания степени выступает число 16, а цифры от A до F заменяются десятичными числами от 10 до 15.
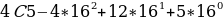
Максимальное двухразрядное число, которое можно получить с помощью шестнадцатеричной записи, – это число FF.
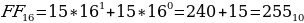
О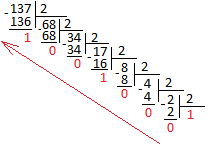 дним из алгоритмов перевода десятичного числа в двоичное является деление нацело на два с последующим "сбором" двоичного числа из остатков. Переведем разобранное уже нами число 137 в двоичное представление.
дним из алгоритмов перевода десятичного числа в двоичное является деление нацело на два с последующим "сбором" двоичного числа из остатков. Переведем разобранное уже нами число 137 в двоичное представление.
Получаем, что 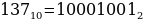
Преобразование десятичного числа в восьмеричное также похоже на перевод в двоичное, за исключением того, что делить надо на 8
Для перевода чисел из десятичной системы счисления в шестнадцатеричную используют тот же "алгоритм замещения", что и при переводе из десятичной системы счисления в двоичную и восьмеричную, только в качестве делителя используют 16
Перевод двоичного в шестнадцатеричную
При переводе двоичного числа в шестнадцатеричное, первое разбивается на группы по четыре разряда, начиная с конца. В случае, если количество разрядов не кратно четырем, первая четверка дописывается нулями впереди. Каждой четверке соответствует одноразрядное число шестнадцатеричной системы счисления.
| Двоичное число | Шестнадцатеричное число |
| 0000 | 0 |
| 0001 | 1 |
| 0010 | 2 |
| 0011 | 3 |
| 0100 | 4 |
| 0101 | 5 |
| 0110 | 6 |
| 0111 | 7 |
| 1000 | 8 |
| 1001 | 9 |
| 1010 | A |
| 1011 | B |
| 1100 | C |
| 1101 | D |
| 1110 | E |
| 1111 | F |
Пример:
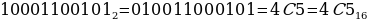
Теперь попробуем прорешать Задание №10 из ОГЭ
№ 10324
Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите максимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.
3816, 758, 1101002.
Решение:
Переведем каждое число в десятичную систему счисления. Алгоритм как это делать представлен выше в теории.
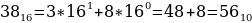
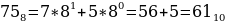
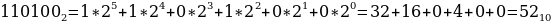
Таким образом, наибольшим среди этих трех чисел является чисто 61.
Ответ: 61.
№ 10325
Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите максимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.
1416, 268, 110002.
Решение:
Переведем каждое число в десятичную систему счисления. Алгоритм как это делать представлен выше в теории.
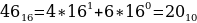
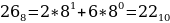
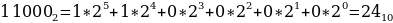
Таким образом, наибольшим среди этих трех чисел является чисто 24.
Ответ: 24.
№ 10329
Среди приведённых ниже трёх чисел, записанных в различных системах счисления, найдите минимальное и запишите его в ответе в десятичной системе счисления. В ответе запишите только число, основание системы счисления указывать не нужно.
4116, 778, 10000102.
Решение:
Переведем каждое число в десятичную систему счисления. Алгоритм как это делать представлен выше в теории.
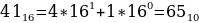
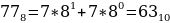
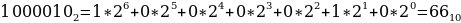
Таким образом, наименьшим среди этих трех чисел является чисто 63.
Ответ: 63.





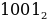 .
.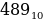 .
.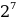 + 0 *
+ 0 *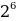 + 0 *
+ 0 *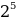 + 0 *
+ 0 * 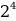 + 1 *
+ 1 * 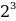 + 0 *
+ 0 * 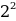 + 0 *
+ 0 * 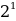 + 1 *
+ 1 * 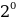
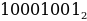 =
= 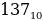
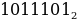 =
= 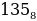
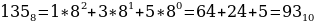
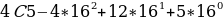
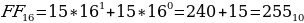
 дним из алгоритмов перевода десятичного числа в двоичное является деление нацело на два с последующим "сбором" двоичного числа из остатков. Переведем разобранное уже нами число 137 в двоичное представление.
дним из алгоритмов перевода десятичного числа в двоичное является деление нацело на два с последующим "сбором" двоичного числа из остатков. Переведем разобранное уже нами число 137 в двоичное представление.