Статистические характеристики

Элементы статистики

Автор: Софронова Наталия Андревна,

учитель математики МОУ «Упшинская ООШ»

Оршанского района Республики Марий Эл

( К учебникам Ю.А.Макарычева Алгебра 7 и Алгебра 8)

Среднее арифметическое

12 семиклассников заметили время (в минутах), затраченное на выполнение домашнего задания по алгебре .

Получили следующие данные: 23, 18, 25, 20, 25, 25, 32, 37, 34, 26, 34, 25.

Сколько минут в среднем затратили учащиеся на выполнение задания по алгебре?

Число 27 называют средним арифметическим рассматриваемого ряда чисел.

Средним арифметическим ряда чисел называется частное от деления суммы этих чисел на число слагаемых .

Среднее арифметическое

Среднее арифметическое представляет собой то значение величины, которое получается, когда сумма всех наблюдаемых значений мысленно распределяется поровну между единицами наблюдения.

• Средняя скорость движения автомобиля.
• Средний балл в аттестате выпускника Петрова
• Средняя оценка выступления фигуристки на чемпионате России.

Иногда вычисление среднего арифметического не дает полезной информации: средний размер обуви учащихся школы

Размах ряда

Время (в минутах), затраченное на выполнение домашнего задания по алгебре 12-тью семиклассниками : 23, 18 , 25, 20, 25, 25, 32, 37 , 34, 26, 34, 25.

В среднем учащиеся на выполнение задания по алгебре затратили 27 минут.

Однако видно, что время, затраченное на выполнение д/з некоторыми учащимися, существенно отличается от 27 минут.

Наибольшее расход времени равен 37 минут.

Наименьший расход – 18 минут.

Разность между наибольшим и наименьшим расходом времени составляет 37 – 18 = 19 минут.

В этом случае говорят, что размах ряда равен 19.

Размахом ряда чисел называется разность между наибольшим и наименьшим из этих чисел.

Мода

При анализе сведений о времени, затраченном семиклассниками на выполнение домашнего задания по алгебре, нас могут интересовать не только среднее арифметическое и размах полученного ряда данных, но и другие показатели.

Интересно, например, знать, какой расход времени является типичным для выделенной группы учащихся, то есть какое число встречается в ряду чаще всего.

Время (в минутах), затраченное на выполнение домашнего задания по алгебре 12-тью семиклассниками : 23, 18, 25, 20, 25, 25, 32, 37, 34, 26, 34, 25.

Нетрудно заметить, что таким числом является число 25.

Говорят, что число 25 – мода рассматриваемого ряда

Модой ряда чисел называется число, которое встречается в данном ряду чаще других.

Мода

Ряд чисел может иметь более одной моды, а может не иметь моды совсем.

Ряд чисел 47, 46, 50, 52, 47, 52, 49, 45, 43, 53, 53, 47, 52 имеет две моды – …. и …...

В ряду чисел 69, 68, 66, 70, 67, 62, 71, 74, 63, 73, 72 моды нет.

Моду ряда данных обычно находят, когда хотят выявить некоторый типичный показатель. Например, если изучают данные о размере мужских сорочек, проданных в определенный день в универмаге, то удобно воспользоваться таким показателем как мода, который характеризует размер, пользующийся наибольшим спросом.

Пример

Пусть проводят учет деталей, изготовленных за смену рабочими одной бригады (в бригаде 21 рабочий)

Получили такой ряд данных:

36, 35, 35, 36, 37, 37, 36, 37, 38, 36, 36, 36, 39, 39, 37,39, 38, 38, 36, 39, 36.

Найдем среднее арифметическое, размах и моду.

Составим упорядоченный ряд:

35, 35, 36, 36, 36, 36, 36, 36, 36, 36, 37, 37, 37, 37, 38, 38, 38, 39, 39, 39, 39.

Среднее арифметическое:

Размах ряда равен 39 – 35 = 4.

Мода данного ряда равна 36

Медиана

• В таблице показан расход электроэнергии в январе жильцами девяти квартир.

• Составим из данных таблицы упорядоченный ряд:
• 64, 72, 72, 75, 78 , 82, 85, 91, 93.
• Нетрудно заметить, что в середине ряда расположено число 78 .
• Говорят, что число 78 является срединным числом или медианой рассматриваемого упорядоченного ряда .

№ кв.

1

Квт/ч

85

2

64

3

78

4

5

93

72

6

7

91

72

8

9

75

82

Медиана

• В таблице показан расход электроэнергии в январе жильцами десяти квартир.

• Составим из данных таблицы упорядоченный ряд:
• 64, 72, 72, 75, 78 , 82 , 83, 85, 91, 93.
• Заметим, что в середине ряда расположены два числа 78 и 82 .
• Их среднее арифметическое (78 + 82) : 2 равно 80. Это число , не являясь членом ряда, разбивает ряд на две одинаковые по численности группы – слева от него находятся пять членов ряда и справа тоже пять членов ряда:
• 64, 72, 72, 75, 78 , 80, 82 , 83, 85, 91, 93.

• Число 80 в этом случае считают медианой рассматриваемого упорядоченного ряда .

№ кв.

1

Квт/ч

2

85

3

64

4

78

5

93

72

6

7

91

8

72

9

75

10

82

83

Медиана

Медианой упорядоченного ряда чисел с нечетным числом членов называется число, записанное посередине,

а медианой упорядоченного ряда чисел с четным числом членов называется среднее арифметическое двух чисел , записанных посередине.

Статистические исследования

• Целенаправленный сбор информации об изучаемом явлении или процессе (этап статистического наблюдения).
• Обобщение и систематизация данных.

Частота события

• 40 учащихся 8 класса выполняли тестовую работу из 9 заданий.

Результат : количество выполненных заданий каждым учащимся:

6,5,4,0,4,5,7,9,1,6,8,7,9,5,8,6,7,2,5,7,

6,3,4,4,5,6,8,6,7,7,4,3,5,9,6,7,8,6,9,8.

Упорядоченный ряд :

0,1,2,3,3,4,4,4,4,4,5,5,5,5,5,5,6,6,6,6,6,6,6,67,7,7,7,7,7,7,8,8,8,8,8,9,9,9,9.

Таблица частот

Упорядоченный ряд:

0,1,2,3,3,4,4,4,4,4,5,5,5,5,5,5,6,6,6,6,6,6,6,6,

7,7,7,7,7,7,7,8,8,8,8,8,9,9,9,9.

Число верно выполненных заданий

Частота события

0

1

1

1

2

1

3

2

4

5

5

6

6

8

7

7

8

9

5

4

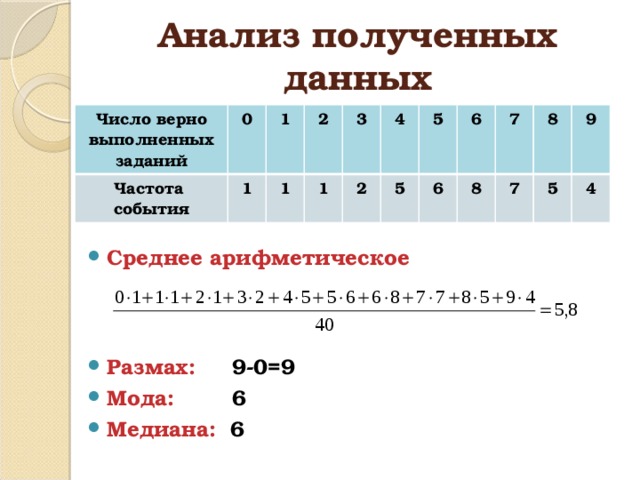
Анализ полученных данных

Число верно выполненных заданий

0

Частота события

1

1

2

1

3

1

4

2

5

5

6

6

7

8

8

7

9

5

4

• Среднее арифметическое

• Размах: 9-0=9
• Мода: 6
• Медиана: 6

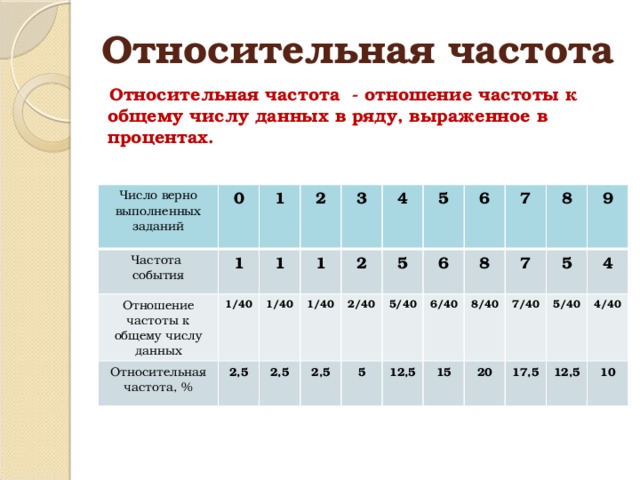
Относительная частота

Относительная частота - отношение частоты к общему числу данных в ряду, выраженное в процентах.

Число верно выполненных заданий

0

Частота события

1

1

Отношение частоты к общему числу данных

2

1/40

Относительная частота, %

1

1/40

1

2,5

3

4

1/40

2

2,5

2/40

5

5

2,5

6

5/40

5

6

8

6/40

7

12,5

8

8/40

7

15

7/40

5

20

9

5/40

17,5

4

4/40

12,5

10

Интервальный ряд

На партии из 50 электроламп изучали продолжительность их горения в часах. По результатам была составлена таблица:

Продолжительность горения в часах

Частота

0-200

1

200-400

3

400-600

5

600-800

9

800-1000

16

1000-1200

9

1200-1400

5

1400-1600

2

Анализ данных

Размах - ? Мода - ? Медиана - ?

Средняя продолжительность горения - ?

Продолжительность горения в часах

Середина интервала

0-200

200-400

100

Частота

300

1

400-600

3

500

600-800

700

800-1000

5

9

900

1000-1200

1100

16

1200-1400

9

1300

1400-1600

1500

5

2