
 Стереометрия 10 класс
Стереометрия 10 класс
Предмет стереометрии Аксиомы стереометрии Некоторые следствия из аксиом
Содержание сборника:
Предмет стереометрии
Конспект……………………………………….…………………. 2
Тест 1…………………………………………................. 5
Решение (тест 1)……………………………………………… 6
Аксиомы стереометрии
Конспект………………………………………………………..… 8
Задачи………………………………..……................... 9
Тест 2…………………………………………………….…………. 11
Решение (тест 2)………….….………………..…………. 13
Некоторые следствия из аксиом
Конспект………………………………………………………..… 15
Задачи…………………..………………………………..……... 17
Дополнительные задачи…………………….…………. 21
Решение (дополнительные задачи)…..…………. 23
Тест 3……………………………………………………………….. 25
Решение (Тест 3)…………………………………………….. 29
Обобщение по теме «Аксиомы стереометрии и некоторые следствия из них»
Конспект………………………………………………………..… 33
Тест 4……………………………………………………..……... 34
Решение (Тест 4) 36
Тест 5 40
Решение (Тест 5) 42
Предмет стереометрии
ГЕОМЕТРИЯ
Планиметрия
раздел геометрии, изучающий свойства фигур на плоскости.
Стереометрия
раздел геометрии, изучающий свойства фигур в пространстве.
Основные: точка, прямая
Луч, отрезок, угол
Треугольник
Изучаемые фигуры
 Основные: точка, прямая, плоскость
Основные: точка, прямая, плоскость
Многогранники: Куб, призма, пирамида
Параллелограмм (частные случаи: квадрат, прямоугольник, ромб)
Трапеция
Многоугольник
Окружность, круг
Тела вращения: цилиндр, конус, шар
Исследуя реальные предметы, геометрия рассматривает только их форму и взаимное расположение, отвлекаясь от других свойств предметов, таких как плотность, вес, цвет. Это позволяет перейти от пространственных отношений между реальными объектами к любым отношениям и формам, возникающим при рассмотрении однородных объектов, и сходным с пространственными.

При изучении пространственных фигур пользуются их изображениями на чертеже.
Представление о плоскости дает гладкая поверхность стола или стены. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.
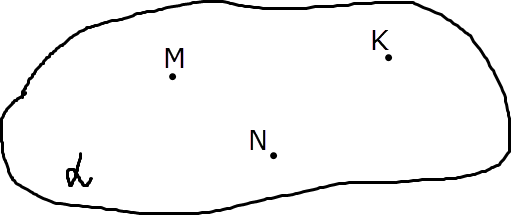

Обозначение плоскости - , ,
MNK .
Обозначения
A a B a A
B
Точка A
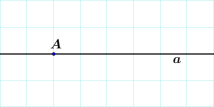 принадлежит прямой a
принадлежит прямой a
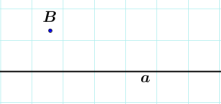 Точка B не принадлежит
Точка B не принадлежит
прямой a
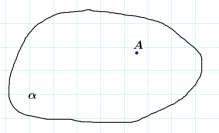 Точка A
Точка A
принадлежит плоскости
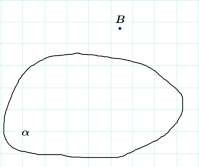
Точка B не принадлежит
плоскости
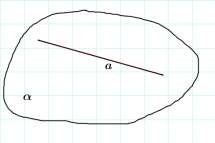
a
b
Прямая a лежит в плоскости
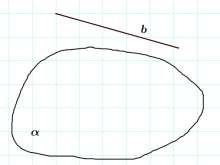
Прямая b не лежит в плоскости
b A
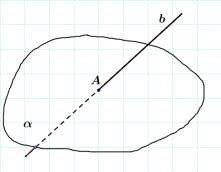
Прямая b пересекает плоскость
в точке A
c
Плоскости
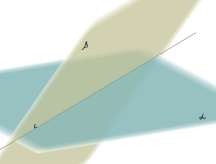 и
и
пересекаются по прямой c
Планиметрия – это раздел геометрии, изучающий …
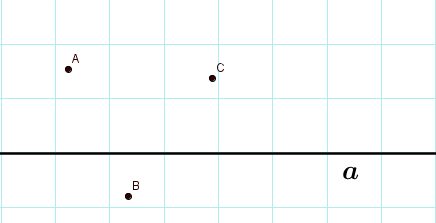
Изобразите прямую a и точки А, В и С, не принадлежащие данной прямой. Сделайте необходимые записи.
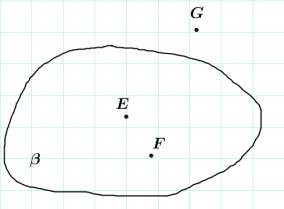
Изобразите плоскость , точки Е, F, принадлежащие ей, и точку G, ей не принадлежащую. Сделайте необходимые записи.
Изобразите прямую а, лежащую в плоскости . Сделайте необходимую запись.
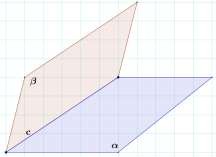
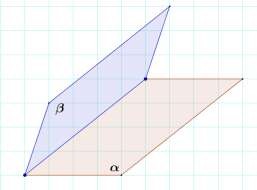
Изобразите две пересекающиеся плоскости и . Сделайте необходимую запись.
Стереометрия – это раздел геометрии, изучающий …
Изобразите две прямые a и b, пересекающиеся в точке О, и точки А, В и С так, чтобы точка А
принадлежала прямой а, точка В принадлежала прямой b, точка С не принадлежала этим прямым.
Сделайте необходимые записи.
Изобразите плоскость , не принадлежащие ей точки K, L и принадлежащую ей точку M. Сделайте необходимые записи.
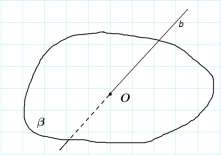
Изобразите прямую b, пересекающую плоскость в точке О. Сделайте необходимую запись.
Изобразите три пересекающиеся по прямой а плоскости , и . Сделайте необходимую запись.
Планиметрия – это раздел геометрии, изучающий свойства фигур на плоскости.
Aa, Ba, C a
E , F , G
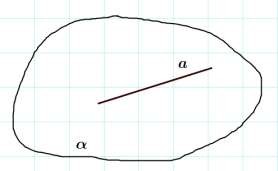
 a
a
Стереометрия – это раздел геометрии, изучающий свойства фигур в пространстве.
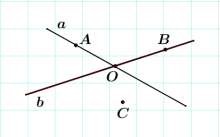
Aa,
Bb,
Ca,
Cb,
a b O
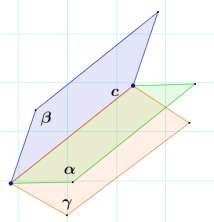
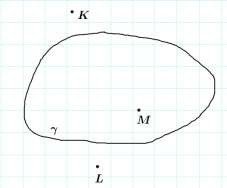
 3. M , K , L
3. M , K , L
4. b O
5. c
Аксиомы стереометрии
Аксиомы геометрии представляют собой исходные положения, на основе которых строится вся геометрия, т.е. путем логических рассуждений устанавливаются свойства геометрических фигур.
Основные свойства точек, прямых и плоскостей, касающихся их взаимного расположения, выражены в аксиомах.
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
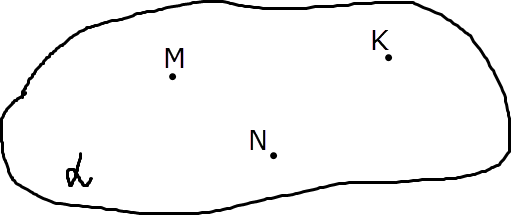

Плоскость (MNK)
Сколько плоскостей можно провести через
три точки, лежащие на одной прямой?
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
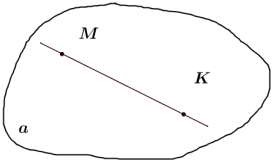
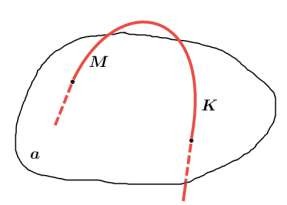
МК – кривая.
Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
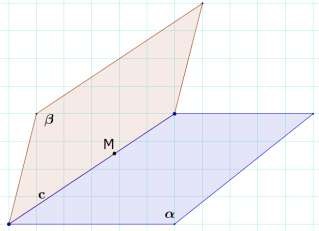
Задача №1
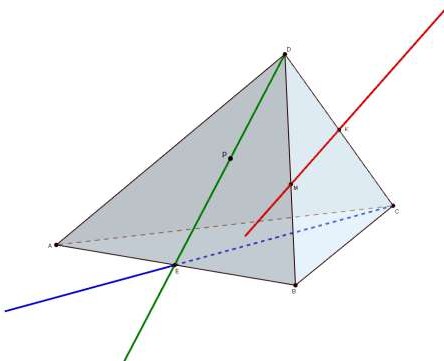 Назовите:
Назовите:
а) плоскости, в которых лежат прямые PE, MK, DB, AB, EC;
б) точки пересечения прямой DK с плоскостью АВС, прямой СЕ с плоскостью ADB;
в) точки, лежащие в плоскостях ADB и DBC;
г) прямые, по которым пересекаются плоскости ABC и DCB, ABD и CDA, PDC и ABC;
Пересекаются ли прямые МК
и АС, МК и ВС?
Задача №2
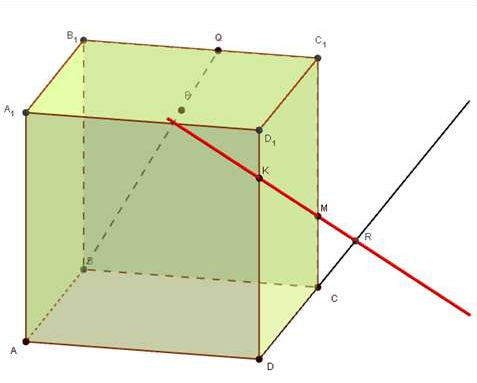 Назовите:
Назовите:
а) точки, лежащие в плоскостях
DCC1 и BQC ;
б) плоскости, в которых лежит
прямая
AA1 ;
в) точки пересечения прямой MK с плоскостью ABD , прямых DK и BP с
плоскостью A1B1C1 ;
г) прямые, по которым пересекаются плоскости
AA1B1
и ACD ,
PB1C1 и ABC ;
д) точки пересечения прямых
MK и DC ,
C1M и DC .
B1C1
и BP ,
Пересекаются ли прямые и KM , BQ и KM ?
A1D1
Каково взаимное положение двух прямых в пространстве. Если они имеют две общие точки?
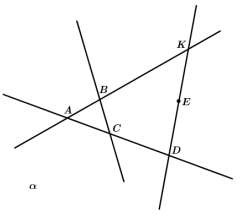 Три точки в пространстве не определяют положение плоскости, которая проходит через них. Как расположены эти точки?
Три точки в пространстве не определяют положение плоскости, которая проходит через них. Как расположены эти точки?
Точки А, В и С принадлежат плоскости . Принадлежит ли плоскости точка E?
Могут ли вершины замкнутой ломаной линии, состоящей из трех звеньев, не принадлежать одной плоскости?
Точка О – центр окружности, описанной около треугольника АВС. Принадлежит ли точка С плоскости, в которой лежат точки А, В и О?
Могут ли две различные плоскости иметь только одну общую точку?
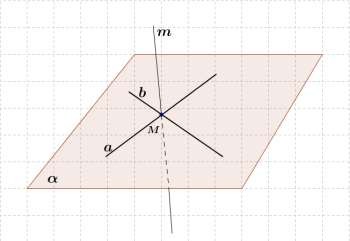
Плоскости и пересекаются по прямой m. Прямая a принадлежит плоскости и пересекает плоскость в точке M. Принадлежит ли точка М прямой m? Сделайте чертеж.
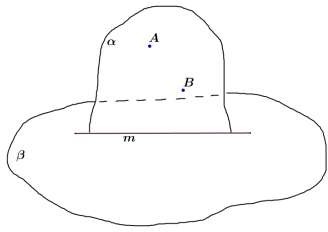 Постройте точку пересечения прямой AB с плоскостью (точки A и B принадлежат ).
Постройте точку пересечения прямой AB с плоскостью (точки A и B принадлежат ).
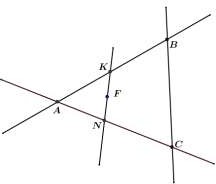 Могут ли две различные прямые в пространстве иметь более одной общей точки?
Могут ли две различные прямые в пространстве иметь более одной общей точки?
Как расположены две плоскости, которые имеют три общие точки, не лежащие на одной прямой?
Точки А, В и С принадлежат плоскости . Принадлежит ли плоскости точка F?
Могут ли вершины замкнутой ломаной линии, состоящей из четырех звеньев, не принадлежать одной плоскости?
Точка О – центр окружности, описанной около четырехугольника АВСD. Точки А, О и С принадлежат плоскости. Принадлежит ли этой плоскости вершина D?
Могут ли две различные плоскости иметь только две общие точки?
Даны две пересекающиеся плоскости и . Прямая a принадлежит плоскости и пересекает плоскость в точке А. Прямая b принадлежит плоскости и пересекает плоскость в точке В. Сделайте чертеж и назовите линию пересечения плоскостей и .
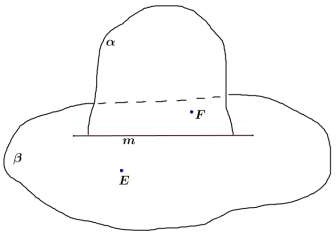 Постройте точку пересечения прямой EF с плоскостью (точки E и F принадлежат ).
Постройте точку пересечения прямой EF с плоскостью (точки E и F принадлежат ).
 E ?
E ?
Решение:
A, B AB (аксиома 2)
A , C AC (аксиома 2)
AC d D D
DK (аксиома 2)
Нет. Т.к. вершины замкнутой ломаной, состоящей из трех звеньев – это три точки, не лежащие на одной прямой, значит, по аксиоме 1 существует единственная плоскость, которой принадлежат все
звенья этой ломаной.
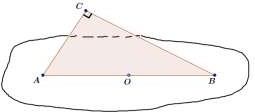 Если треугольник прямоугольный, то центр описанной
Если треугольник прямоугольный, то центр описанной
окружности - т. О лежит на середине гипотенузы АВ. Значит, через три точки, лежащие на одной прямой А-О-В можно провести сколько угодно плоскостей, которые не обязательно проходят через точку С.
Нет. Т.к. по аксиоме 3, если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой расположены все общие точки этих плоскостей.
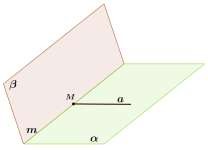 7. Дано: m, a , a M
7. Дано: m, a , a M
M m ?
Решение:
М – общая точка плоскостей и .
По условию прямая m – прямая пересечения этих плоскостей, значит M m по аксиоме 3.
8. m
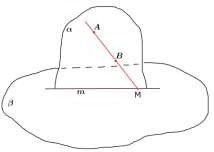 AB , AB m M
AB , AB m M
AB M
Нет.
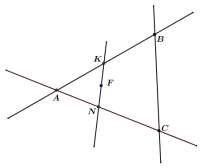 Они совпадают.
Они совпадают.
Дано:
A, B,C
F ?
Решение:
A, B AB (аксиома 2)
A , C AC (аксиома 2)
AB KN K K
AC KN N N
KN (аксиома 2)
F KN F .
Да.
 Т.к. вершины замкнутой ломаной, состоящей из четырех
Т.к. вершины замкнутой ломаной, состоящей из четырех
звеньев – это четыре точки, три из которых, не лежащие на одной прямой, по аксиоме 1, задают единственную плоскость, а четвертая может этой плоскости не
принадлежать.
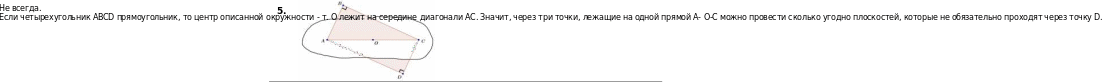
6. Нет. Т.к. по аксиоме 3, если две различные плоскости имеют общую точку, то они имеют общую прямую, на которой расположены все общие точки этих плоскостей.

8.
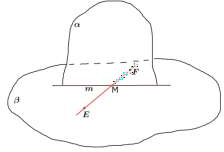 m
m
FM , FM m M
EF M
Некоторые следствия из аксиом
В пространстве существует бесконечно много плоскостей, и в каждой плоскости справедливы все аксиомы и теоремы планиметрии. Признаки равенства и подобия
треугольников, известные из курса планиметрии, справедливы и для треугольников, расположенных в разных плоскостях.
Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
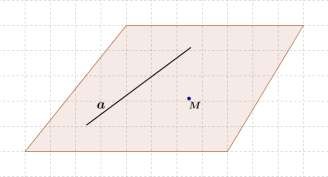 Дано: a прямая, M a .
Дано: a прямая, M a .
Доказать: Существует плоскость такая,
что a и M и
- единственная.
Док-во:
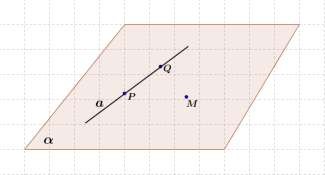 P a, Q a , M a . Значит, P,Q, M - не
P a, Q a , M a . Значит, P,Q, M - не
лежат на одной прямой. По аксиоме 1, существует некая плоскость .
P a, Q a , то по аксиоме 2, a .
Плоскость , проходящая через прямую
a и точку M , совпадает с плоскостью,
проходящей через точки P,Q, M и она
единственная по аксиоме 1.
Ч.т.д.
Через две пересекающиеся прямые проходит плоскость, и притом только одна.
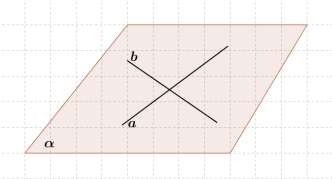 Дано: a b M .
Дано: a b M .
Доказать: Существует плоскость такая,
что a и b и
- единственная.
Доказательство:
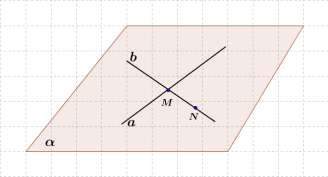 N b, N a , следовательно, через прямую a и точку N , не лежащую на
N b, N a , следовательно, через прямую a и точку N , не лежащую на
ней, проходит плоскость (теорема 1).
M b, N b , значит, по аксиоме 2,
MN b .
Итак, a и b .
Любая плоскость, проходящая через прямые a и b , проходит через точку
N . Она единственная и совпадает с . Т.к. по теореме 1 через прямую и точку, не лежащую на ней проходит только одна плоскость.
Ч.т.д.
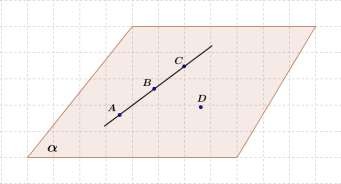 Дано: A, B,C, D одной плоскости.
Дано: A, B,C, D одной плоскости.
а) Могут ли какие-то три из них лежить на одной прямой?
Нет, т.к. через прямую и точку, не лежащую на ней, можно провести
плоскость и все точки будут принадлежать
плоскости. А по условию A, B,C, D одной плоскости.
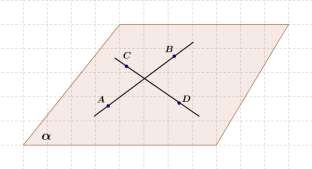 б) Могут ли прямые AB и CD пересекаться?
б) Могут ли прямые AB и CD пересекаться?
Нет, т.к. две пересекающиеся прямые задают плоскость по теореме 2 и все точки будут принадлежать плоскости. А по
условию A, B,C, D одной плоскости.
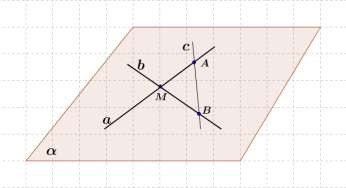 Дано: a b M , c a A, c b B .
Дано: a b M , c a A, c b B .
Доказать:
a, b, c .
Доказательство:
a b (теорема 2).
a , c a A A
b , c b B B
AB c
(аксиома 2).
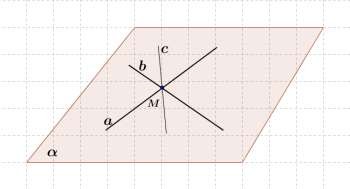 Лежат ли в одной плоскости все прямые, проходящие через точку M ?
Лежат ли в одной плоскости все прямые, проходящие через точку M ?
Нет.
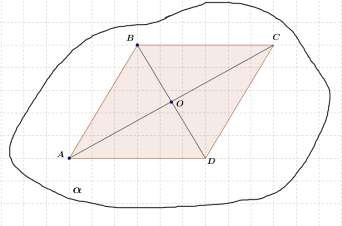 Дано: ABCD параллелограмм,
Дано: ABCD параллелограмм,
A, B,O .
Доказать: C , D . Доказательство:
A O B O
AO
BO
C AO C
D BO D
Ч.т.д.
Задача №12
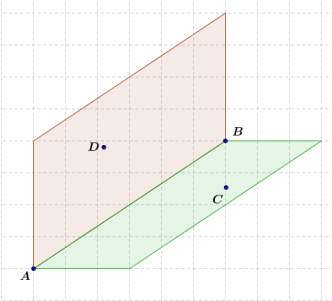 Дано:
Дано:
Да.
A, B,C, D одной плоскости.
ABC ABD ?
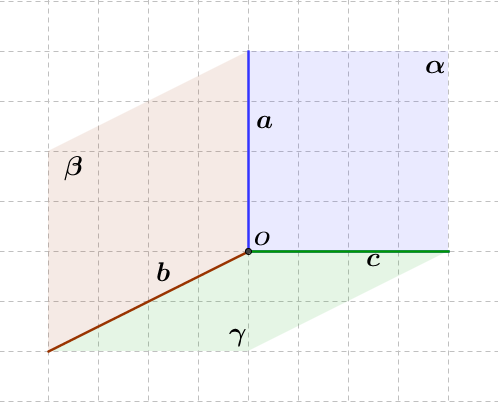 Дано: a,b, c проходят через одну точку O . Через каждуе две из них проведена Плоскость.
Дано: a,b, c проходят через одну точку O . Через каждуе две из них проведена Плоскость.
Сколько всего проведено плоскостей?
а) Три, если прямые не лежат в одной плоскости;
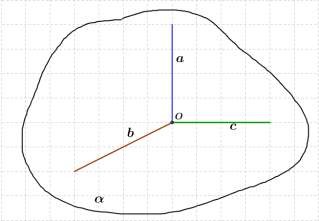 б) Одна, если прямые лежат в одной плоскости.
б) Одна, если прямые лежат в одной плоскости.
№ Задача
Укажите плоскости которым принадлежит прямая
АВ.
Укажите плоскости которым принадлежит точка
F.
Укажите плоскости которым принадлежит точка
C.
Укажите прямую пересечения плоскостей АВС и
ACD.
Укажите прямую пересечения плоскостей АВD и
Задача
DCF.
Принадлежит ли точка F плоскости ? Ответ обоснуйте.
Даны точки А, В, С, D, не лежащие в одной плоскости.
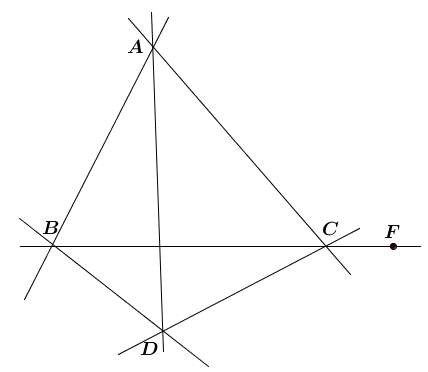
Точка М лежит вне плоскости , а точки А, В и С
принадлежат этой плоскости.

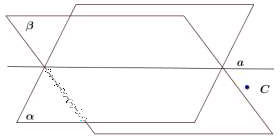 Плоскости и пересекаются по прямой а.
Плоскости и пересекаются по прямой а.
Может ли точка С принадлежать плоскостям и
. Ответ обоснуйте.
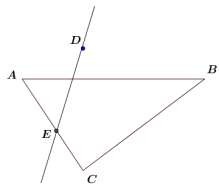 Точка D лежит вне плоскости АВС. Пересекаются ли прямые DE и ВС?
Точка D лежит вне плоскости АВС. Пересекаются ли прямые DE и ВС?



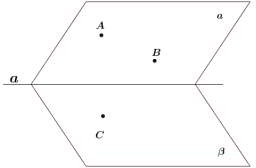 Плоскости и пересекаются по прямой а. Точки А и В принадлежат плоскости , а точка С – плоскости . Постройте прямые пересечения
Плоскости и пересекаются по прямой а. Точки А и В принадлежат плоскости , а точка С – плоскости . Постройте прямые пересечения
плоскости АВС с плоскостями и .
№ Задача
Решение (Дополнительные задачи). Аксиомы стереометрии и следствия из них
АВС, АВD Даны точки А, В, С, D, не лежащие в одной плоскости.
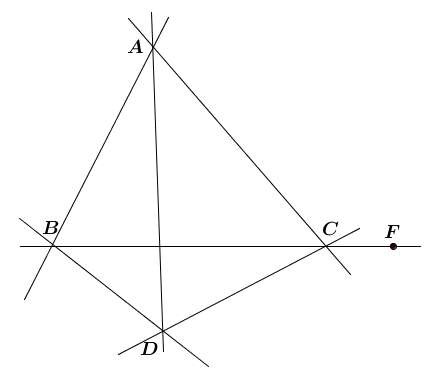 АВС, BCD
АВС, BCD
АВС, ВСD, ADC
АС
ВD
Задача
Нет, т.к. F MB и MB B . Точка М лежит вне плоскости , а точки А, В и С
принадлежат этой плоскости.
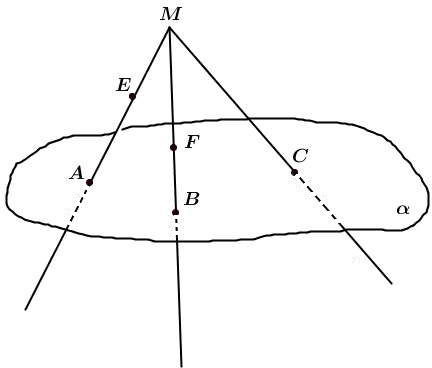 Точки А и В – общие точки плоскостей и АВМ, значит по аксиоме 3 эти две плоскости
Точки А и В – общие точки плоскостей и АВМ, значит по аксиоме 3 эти две плоскости
пересекаются по прямой АВ.
ВМ
Да, если она совпадет с точкой А.
Нет, т.к. прямая АС пересекает плоскость МВС в точке С.

 Да, если точка С будет принадлежать прямой пересечения плоскостей и , т.е. прямой а.
Да, если точка С будет принадлежать прямой пересечения плоскостей и , т.е. прямой а.
Нет.


m
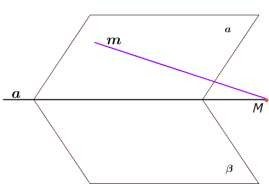 m M
m M
a
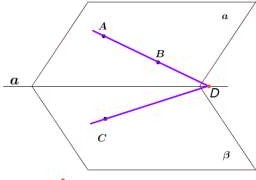 AB a D
AB a D
CD AB ABC ABC AB ABC CD
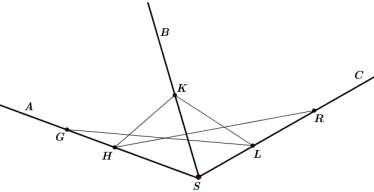
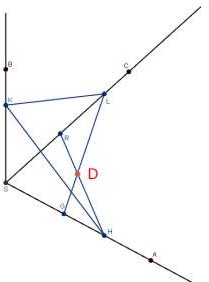
Туго натянутая нить последовательно закреплена в точках G, L, K, H и R, расположенных на стержнях
SA, SB и SC, которые не принадлежат одной плоскости. Отметьте и обозначьте точки, в которых отрезки соприкасаются.
В чем ошибка чертежа? Внесите изменения в чертеж таким образом, чтобы он стал верным.
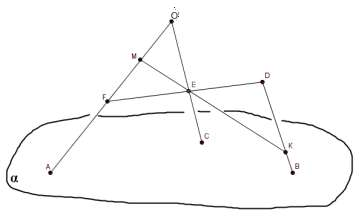
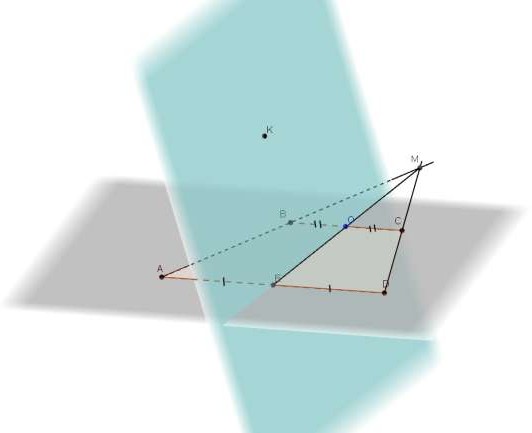
На рисунке изображены пересекающиеся плоскости и . Точки А и В принадлежат плоскости , а точка С лежит в плоскости . Изобразите точку D, принадлежащую плоскости , так, чтобы отрезки
AD и ВС оказались пересекающимися.
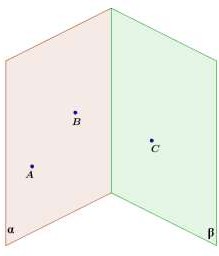
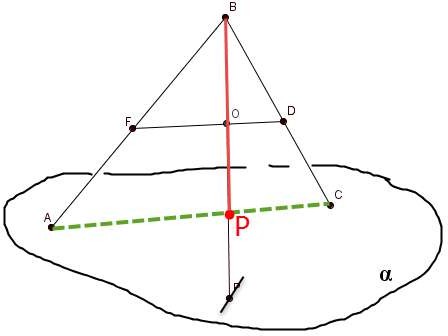
В трапеции ABCD (AD и BC – основания) АВ пересекает CD в точке М. Е – середина AD. O BC . Точка К
расположена вне плоскости трапеции. При каком условии точки К, М, О и Е лежат в одной плоскости?
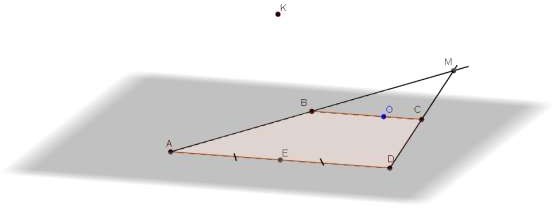
Туго натянутая нить последовательно закреплена в точках G, L, K, H и R, расположенных на стержнях
SA, SB и SC, которые не принадлежат одной плоскости. Отметьте и обозначьте точки, в которых отрезки соприкасаются.
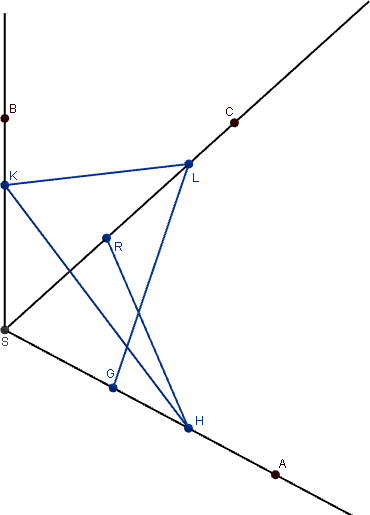
В чем ошибка чертежа? Внесите изменения в чертеж таким образом, чтобы он стал верным.
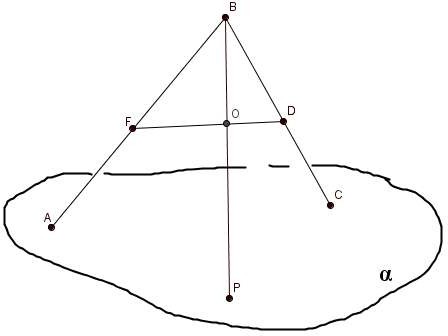
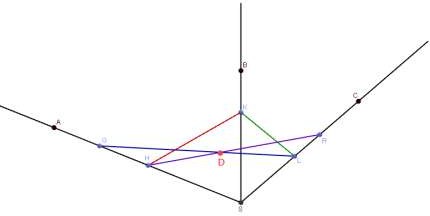
На рисунке изображены пересекающиеся плоскости и . Точки С и D принадлежат плоскости , а точка B лежит в плоскости . Изобразите точку A, принадлежащую плоскости , так, чтобы
отрезки AC и ВD оказались пересекающимися.
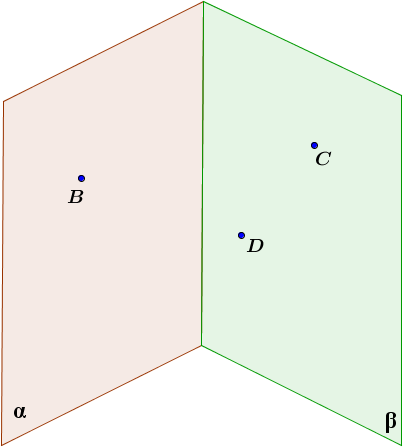
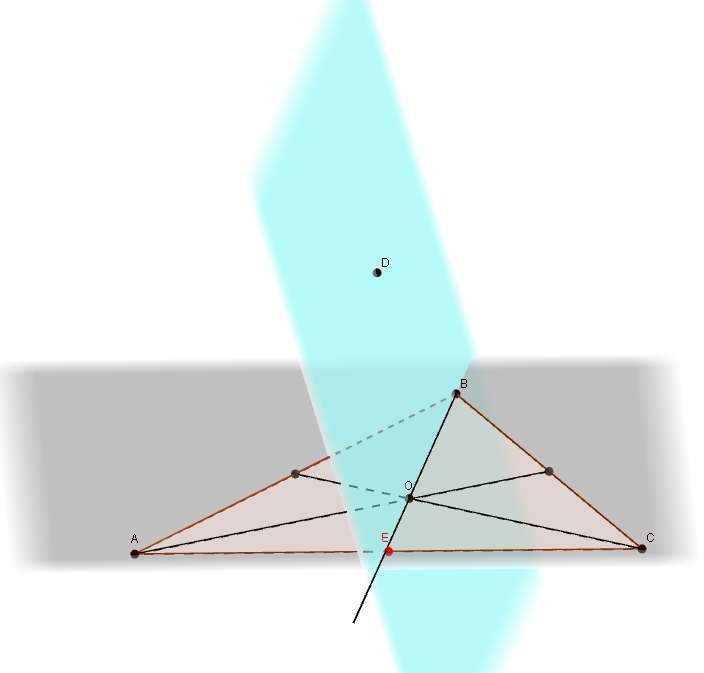
В треугольнике ABC медианы, проведенные к сторонам ВС и АВ, пересекаются в точке О. E AC . Точка D лежит вне плоскости АВС. При каком условии можно провести плоскость через точки D, B, O и Е ?
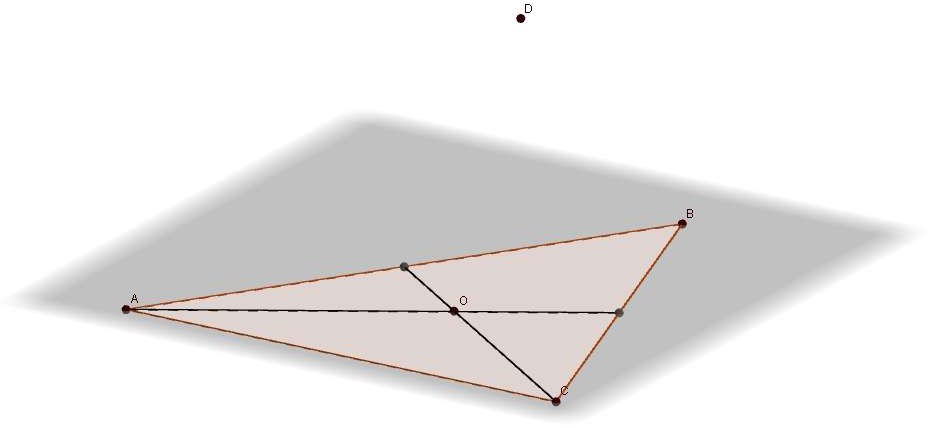
SA SC ASC G, H , L, R ASC GL HR D
(есть видео подсказка)
Все пересекающиеся прямые задают плоскость (АОВ).
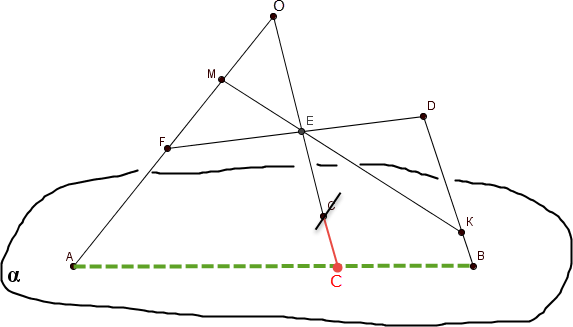
2.
AOB
AB , значит, все общие точки этих плоскостей лежат на этой прямой.
Тогда C AB .
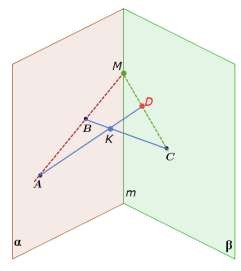
3.
m
AB , AB M , M m CM , CM M
AB CM AMC
D CM
A, B,C, D AMC AD BC
4.
По теореме 1 через прямую МЕ и точку К, не лежащую на ней, можно провести единственную плоскость. Точка О будет лежать в этой же плоскости, если O ME ,
т.е. при условии, что BO OC . (Есть видео подсказка)
1.
SA SC ASC G, H , L, R ASC GL HR D
(есть видео подсказка)
2.
Все пересекающиеся прямые задают плоскость (АВС).
ABC AC , значит, все общие
точки этих плоскостей лежат на этой прямой.
Тогда P AC .
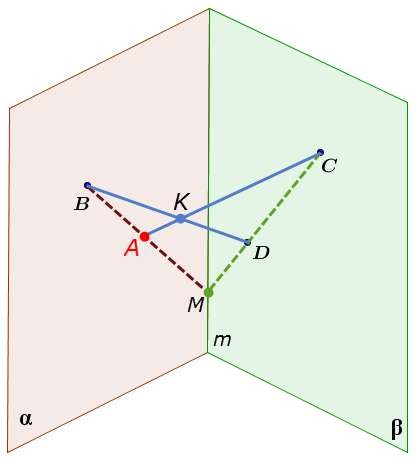
3.
m
CD , CD M , M m BM , BM M
BM CD BMC
A BM
 A, B,C, D BMC AC BD
A, B,C, D BMC AC BD
4.
По теореме 1 через прямую ВО и точку D, не лежащую на ней, можно провести единственную плоскость. Точка E будет лежать в этой же плоскости, если E BO , т.е. при условии, что AE EC . (Есть видео подсказка)
Обобщение по теме
«Аксиомы стереометрии и некоторые следствия из них»
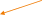
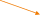
ГЕОМЕТРИЯ
Планиметрия
раздел геометрии, изучающий свойства фигур на плоскости.
Стереометрия
раздел геометрии, изучающий свойства фигур в пространстве.
Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.
Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Вариант 1
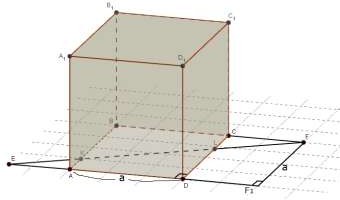
Дан куб ABCDA1B1C1D1 с ребром, равным a . Точка К принадлежит ребру AA1 , точка L - ребру
DD1 . При этом A1K : KA 1: 3, D1L : LD 2 :1 . Проведена прямая KL . Используя рисунок,
ответьте на следующие вопросы.
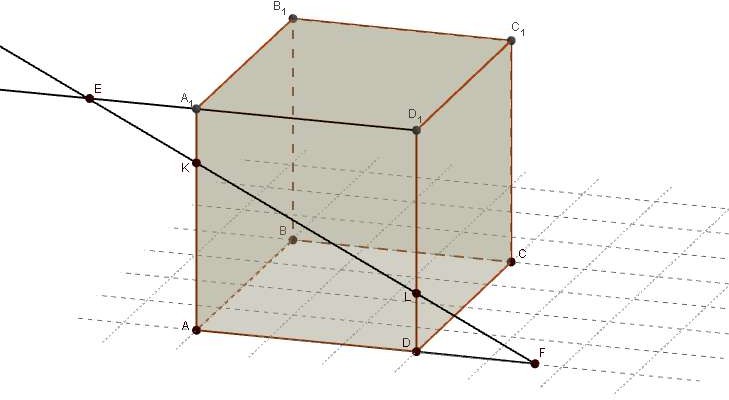
№ Задание:
Укажите точку пересечения прямой KL и плоскости ABD.
Найдите точку пересечения прямых KL и A1D1 .
Укажите линию пересечения плоскостей
A1 AD и
B1EF .
Найдите длину отрезка C1L .
Вычислите длину отрезка KL .
Найдите длину отрезка EF .
Вариант 2
Дан куб ABCDA1B1C1D1 с ребром, равным a . Точка К принадлежит ребру AB , точка L - ребру CD .
При этом
AK : KB 1: 3, CL : LD 1: 4 . Проведена прямая KL . Используя рисунок, ответьте на
следующие вопросы.
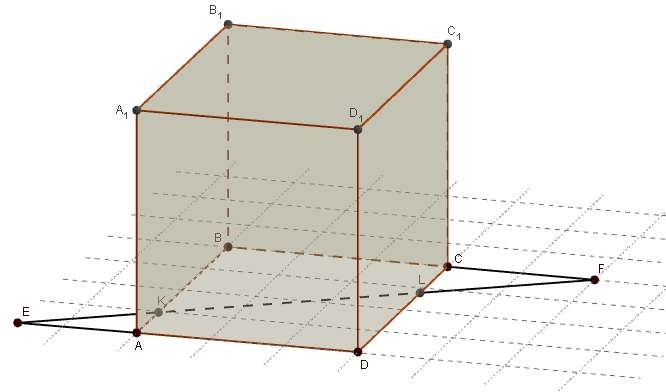
№ Задание:
Укажите точку пересечения прямой KL и плоскости A1D1D .
Найдите точку пересечения прямых KL и ВС.
Укажите линию пересечения плоскостей ABC и B1EF .
Найдите длину отрезка B1K .
Вычислите длину отрезка KL .
Найдите длину отрезка EF .
Вариант 1
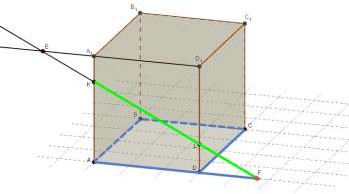 1. Укажите точку пересечения прямой KL и
1. Укажите точку пересечения прямой KL и
плоскости ABD.
KL ABD F , т.к.
KL ADD1
ADD1 ABD AD KL AD F
2. Найдите точку пересечения прямых KL и
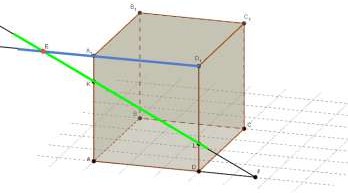 ВС.
ВС.
KL A1D1 E , т.к.
KL; A1D1 ADD1
3. Укажите линию пересечения плоскостей
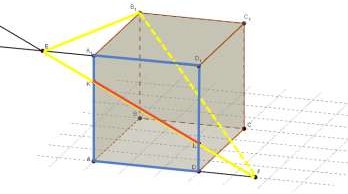 A1AD и B1EF .
A1AD и B1EF .
A1 AD B1EF KL
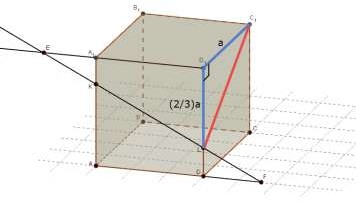 Найдите длину отрезка C1L .
Найдите длину отрезка C1L .
4.
 LD1C1 прямоугольный,
LD1C1 прямоугольный,
D L 2 a .
D1C1 a ,
1 3
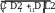 C1L
C1L
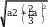
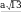
3
5. Вычислите длину отрезка KL .
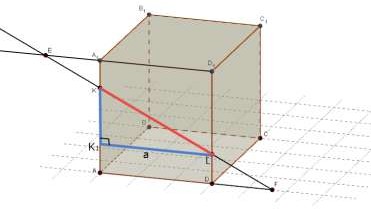 Проведем
Проведем
K1L || AD ,
K1K a .
A K a , DL AK a
1 4 1 3
KK1 AA1 AK1 A1K
a a a 5a
3 4 12
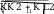
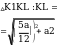
13a 12
KL 13a
12
6. Найдите длину отрезка EF .
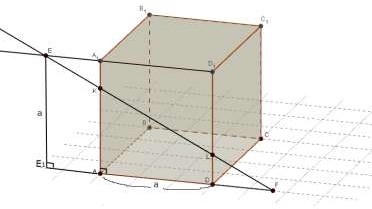 Проведем пересечения с
Проведем пересечения с
EE1 || AA1 EE1 .
и продлим AD до
Рассмотрим подобные треугольники LDF
и KAF .
a
DF DL , x 3
, x 4a , DF 4a

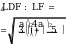 AF AK a x
AF AK a x
3a 5 5
4
13a
15
Рассмотрим подобные треугольники
EE1F и LDF .
13a a
LF LD ,
15 3 , EF 13a
EF EE1
EF a 5
Вариант 2
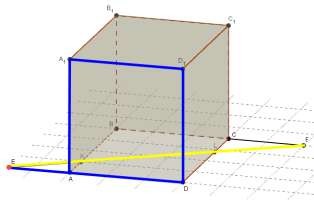 1. Укажите точку пересечения прямой KL и
1. Укажите точку пересечения прямой KL и
плоскости A1D1D .
KL A1D1D E , т.к.
KL ADC
ADC A1D1D AD KL AD E
2. Найдите точку пересечения прямых KL и
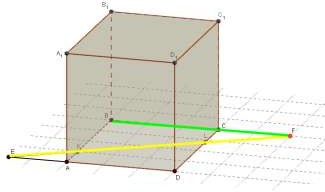 BC.
BC.
KL BC F , т.к.
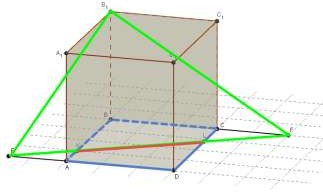 KL; BC ABC
KL; BC ABC
3. Укажите линию пересечения плоскостей
ABC и
B1EF .
ABC B1EF KL
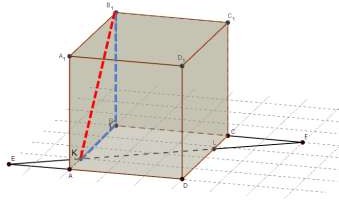 Найдите длину отрезка
Найдите длину отрезка
4.
B1K .
 KBB1 прямоугольный,
KBB1 прямоугольный,
BK 3 a .
4
DD1 a ,
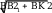
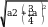 5a
5a
B1K
4
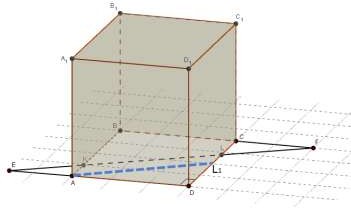 5. Вычислите длину отрезка KL .
5. Вычислите длину отрезка KL .
Проведем
AL1 || KL ,
DL 4a , LL AK a
5 1 4
DL DL LL
4a a 11a .
1 1 5 4 20
KL a
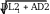
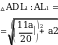
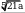
20
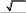 521
521
20
 6. Найдите длину отрезка EF .
6. Найдите длину отрезка EF .
Проведем пересечения с
FF1 || CD и продлим AD до
FF1 .
Рассмотрим подобные треугольники EKA
и ELD .
EA AK ,
a
x 4
, x 5a , EA 5a
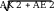
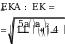 ED DL a x
ED DL a x
4a
5
 521a 44
521a 44
11 11
Рассмотрим подобные треугольники EKA
и EFF1 .
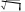
 521a a
521a a
EK
KA ,
44 4 , EF
521a
EF FF1
EF a 4
Вариант 1
В пирамиде SABC все ребра равны a . На ребре АС выбрана точка К, на ребре ВС - точка L . При
этом AK : KC 1: 2, CL : LB 1: 4 . Через точки K, L, S проведена плоскость. Используя рисунок,
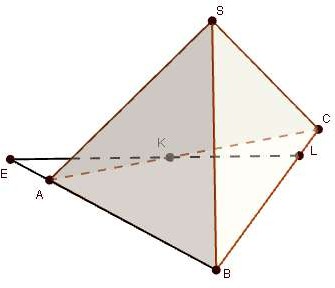 ответьте на следующие вопросы.
ответьте на следующие вопросы.
№ Задание:
Укажите линию пересечения плоскостей SKL и SAB.
Найдите линию пересечения плоскостей SEL и SBC.
Укажите точку пересечения плоскостей АВС, SAC и SBC.
Вычислите площадь треугольника BSL.
Вычислите длину отрезка AE.
Найдите длину отрезка LE.
Вариант 2
В пирамиде SABC все ребра равны a . На ребре АС выбрана точка К, на ребре ВС - точка L . При
этом AK : KC 2:1, CL : LB 3:1. Через точки K, L, S проведена плоскость. Используя рисунок,
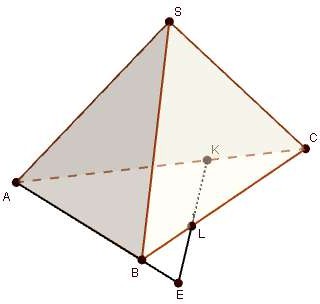 ответьте на следующие вопросы.
ответьте на следующие вопросы.
№ Задание:
Укажите линию пересечения плоскостей SKL и SAB.
Найдите линию пересечения плоскостей SKL и SAC.
Укажите точку пересечения плоскостей SАВ, ABC и SAC.
Вычислите площадь треугольника SLC.
Вычислите длину отрезка BE.
Найдите длину отрезка KE.
Вариант 1
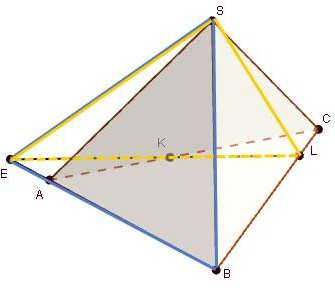 Укажите линию пересечения плоскостей SKL
Укажите линию пересечения плоскостей SKL
и SAB.
SKL SAB SE
Найдите линию пересечения плоскостей SEL
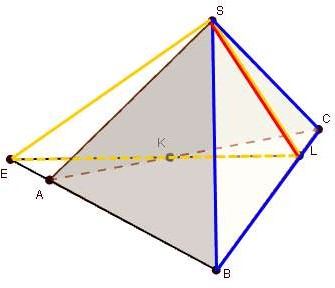 и SBC.
и SBC.
SEL SBC SL
Укажите точку пересечения плоскостей АВС, SAC и SBC.
Все плоскости пересекаются в точке С.
Вычислите площадь треугольника BSL.
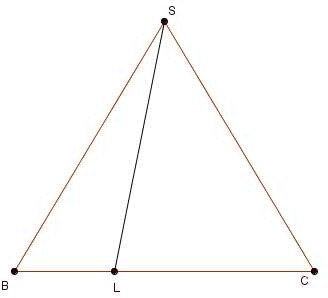
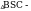 равносторонний
равносторонний
 B 60 , BL 4a , BS a
B 60 , BL 4a , BS a

5
SBSL
1 BL BS sin 60 2
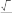
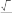 1 a 4 a 3 3 a2
1 a 4 a 3 3 a2
2 5 2 5
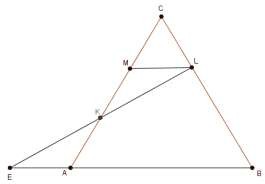
 Вычислите длину отрезка AE.
Вычислите длину отрезка AE.
Рассмотрим
. Проведем
ML || AB ,
 MCL равносторонний.
MCL равносторонний.
CL a , ML CM a
5 5
KM KC CM 2a a 7a
 3 5 15
3 5 15
EAK LMK
a 7a
ML KM ,
5 15 , EA a
EA AK EA a 7
3
Найдите длину отрезка LE.
См. рис. к задаче №5.
 Рассмотрим EBL :
Рассмотрим EBL :
LB 4a , BE EA AB a a 8a , B 60 .
.
5 7 7
По теореме косинусов:
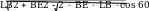
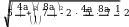 EL
EL
EL
4 79a
 35
35
Вариант 2
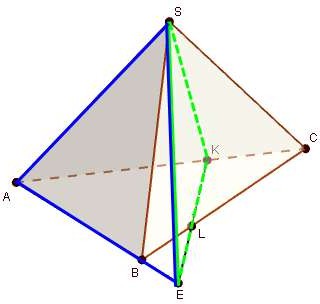 Укажите линию пересечения
Укажите линию пересечения
плоскостей SKL и SAB.
SKL SAB SE
Найдите линию пересечения
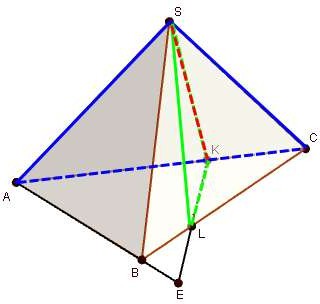 плоскостей SKL и SAC.
плоскостей SKL и SAC.
SKL SAC SK
Укажите точку пересечения плоскостей SАВ, ABC и SAC.
Все плоскости пересекаются в точке А.
Вычислите площадь треугольника
 SLC.
SLC.
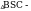 равносторонний
равносторонний
, LC

C 60
3a , SC a

4
SSLC
1 CL CS sin 60 2
1 a 3 a
3 3 3 a2
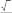
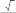 2 4 2 16
2 4 2 16
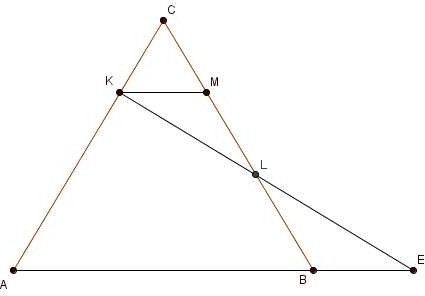 Вычислите длину отрезка BE.
Вычислите длину отрезка BE.
 Рассмотрим ABC . Проведем
Рассмотрим ABC . Проведем
MK || AB , MCK равносторонний.
CM a , MK CK a
3 3
LM LC CM 3a a 5a
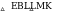 4 3 12
4 3 12
Найдите длину отрезка LE.
См. рис. к задаче №5.
ML KM ,
LB BE
5a 12
a
4
a
3 , BE a BE 5
 Рассмотрим AKE :
Рассмотрим AKE :
AK 2a , AE BE AB a a 6a , B 60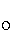 .
.
3 5 5
По теореме косинусов:
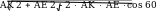
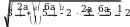 KE
KE
EL
2 61a
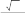 15
15








 Стереометрия 10 класс
Стереометрия 10 класс
 ГЕОМЕТРИЯ
ГЕОМЕТРИЯ 
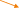 Основные: точка, прямая, плоскость
Основные: точка, прямая, плоскость

 принадлежит прямой a
принадлежит прямой a Точка B не принадлежит
Точка B не принадлежит Точка A
Точка A Точка B не принадлежит
Точка B не принадлежит 
 Прямая b не лежит в плоскости
Прямая b не лежит в плоскости  Прямая b пересекает плоскость
Прямая b пересекает плоскость  и
и 



 a
a 


 3. M , K , L
3. M , K , L




 Назовите:
Назовите: Назовите:
Назовите: Три точки в пространстве не определяют положение плоскости, которая проходит через них. Как расположены эти точки?
Три точки в пространстве не определяют положение плоскости, которая проходит через них. Как расположены эти точки? Постройте точку пересечения прямой AB с плоскостью (точки A и B принадлежат ).
Постройте точку пересечения прямой AB с плоскостью (точки A и B принадлежат ). Могут ли две различные прямые в пространстве иметь более одной общей точки?
Могут ли две различные прямые в пространстве иметь более одной общей точки? Постройте точку пересечения прямой EF с плоскостью (точки E и F принадлежат ).
Постройте точку пересечения прямой EF с плоскостью (точки E и F принадлежат ). Если треугольник прямоугольный, то центр описанной
Если треугольник прямоугольный, то центр описанной 7. Дано: m, a , a M
7. Дано: m, a , a M AB , AB m M
AB , AB m M Они совпадают.
Они совпадают. Т.к. вершины замкнутой ломаной, состоящей из четырех
Т.к. вершины замкнутой ломаной, состоящей из четырех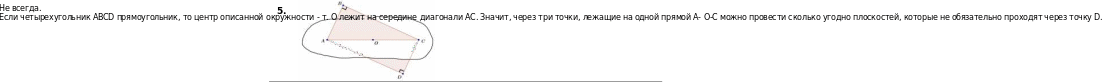

 m
m Дано: a прямая, M a .
Дано: a прямая, M a . P a, Q a , M a . Значит, P,Q, M - не
P a, Q a , M a . Значит, P,Q, M - не Дано: a b M .
Дано: a b M . N b, N a , следовательно, через прямую a и точку N , не лежащую на
N b, N a , следовательно, через прямую a и точку N , не лежащую на Дано: A, B,C, D одной плоскости.
Дано: A, B,C, D одной плоскости. б) Могут ли прямые AB и CD пересекаться?
б) Могут ли прямые AB и CD пересекаться? Дано: a b M , c a A, c b B .
Дано: a b M , c a A, c b B . Лежат ли в одной плоскости все прямые, проходящие через точку M ?
Лежат ли в одной плоскости все прямые, проходящие через точку M ?
 Дано: ABCD параллелограмм,
Дано: ABCD параллелограмм, Дано:
Дано: Дано: a,b, c проходят через одну точку O . Через каждуе две из них проведена Плоскость.
Дано: a,b, c проходят через одну точку O . Через каждуе две из них проведена Плоскость. б) Одна, если прямые лежат в одной плоскости.
б) Одна, если прямые лежат в одной плоскости.

 Плоскости и пересекаются по прямой а.
Плоскости и пересекаются по прямой а. Точка D лежит вне плоскости АВС. Пересекаются ли прямые DE и ВС?
Точка D лежит вне плоскости АВС. Пересекаются ли прямые DE и ВС?


 Плоскости и пересекаются по прямой а. Точки А и В принадлежат плоскости , а точка С – плоскости . Постройте прямые пересечения
Плоскости и пересекаются по прямой а. Точки А и В принадлежат плоскости , а точка С – плоскости . Постройте прямые пересечения АВС, BCD
АВС, BCD Точки А и В – общие точки плоскостей и АВМ, значит по аксиоме 3 эти две плоскости
Точки А и В – общие точки плоскостей и АВМ, значит по аксиоме 3 эти две плоскости

 m M
m M AB a D
AB a D







 Решение (Тест 3). Некоторые следствия из аксиом Вариант 1 1.
Решение (Тест 3). Некоторые следствия из аксиом Вариант 1 1.
 3.
3.  4.
4.  1.
1.  2.
2.  3.
3.  A, B,C, D BMC AC BD
A, B,C, D BMC AC BD
 ГЕОМЕТРИЯ
ГЕОМЕТРИЯ 

 1. Укажите точку пересечения прямой KL и
1. Укажите точку пересечения прямой KL и ВС.
ВС. A1AD и B1EF .
A1AD и B1EF . Найдите длину отрезка C1L .
Найдите длину отрезка C1L .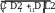 C1L
C1L 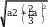
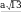
 Проведем
Проведем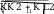
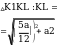
 Проведем пересечения с
Проведем пересечения с
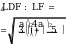 AF AK a x
AF AK a x 1. Укажите точку пересечения прямой KL и
1. Укажите точку пересечения прямой KL и BC.
BC. KL; BC ABC
KL; BC ABC Найдите длину отрезка
Найдите длину отрезка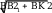
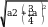 5a
5a 5. Вычислите длину отрезка KL .
5. Вычислите длину отрезка KL .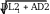
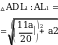
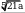
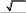 521
521 6. Найдите длину отрезка EF .
6. Найдите длину отрезка EF .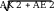
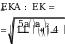 ED DL a x
ED DL a x 521a 44
521a 44
 521a a
521a a ответьте на следующие вопросы.
ответьте на следующие вопросы. ответьте на следующие вопросы.
ответьте на следующие вопросы. Укажите линию пересечения плоскостей SKL
Укажите линию пересечения плоскостей SKL и SBC.
и SBC.
 равносторонний
равносторонний
 1 a 4 a 3 3 a2
1 a 4 a 3 3 a2
 Вычислите длину отрезка AE.
Вычислите длину отрезка AE.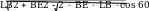
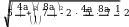 EL
EL  35
35 Укажите линию пересечения
Укажите линию пересечения плоскостей SKL и SAC.
плоскостей SKL и SAC.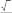
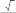 2 4 2 16
2 4 2 16 Вычислите длину отрезка BE.
Вычислите длину отрезка BE. Рассмотрим ABC . Проведем
Рассмотрим ABC . Проведем 4 3 12
4 3 12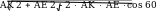
 KE
KE  15
15









