Просмотр содержимого документа
«Сумма пятых степеней.»
Тема: Существуют ли попарно различные натуральные числа  такие, что
такие, что  ?
?
Автор: Мустафаев Рустем Эйвасович, 02.03.1968 Г.Р.
Аннотация: При решении вопроса показано, что данное равенство противоречит закону, по которому образуются степенные ряды Тейлора от линейных функций (значений), расположенных правее, (разложение от крупных чисел до меньших степенных значений) … Применён принцип анализа с использованием меры Хаара.
Ключевые слова: Ϭ-кольцо; компактная группа; степенные значения; мера Хаара; свёртка; приращение.
Решение
Каждое слагаемое можно представить, как сумму основы, корня числа и его прироста (значения увеличения) … За основу возьмём максимальное простое число, образующее значения ( ). При различных членах уравнения различны и их приращения (остатки, в сумме с
). При различных членах уравнения различны и их приращения (остатки, в сумме с  образующие
образующие  ).
).
Если  , то убрав везде “
, то убрав везде “ ”, получим:
”, получим:
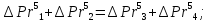




Из этого следует: 2(
Образование суммы “ ” возможно при изначально, вдвое большей суммы “
” возможно при изначально, вдвое большей суммы “ ”, чем в условии задачи, то есть равенство
”, чем в условии задачи, то есть равенство  ,
,
соблюдаться не может. Примеры:
 ;
; 
Основой  и
и  есть общее
есть общее 

 совпадает с
совпадает с 
Определим, как можно представить 8800 в виде “ ”.
”. 
Возьмём 



 нельзя представить пятой степенью натурального числа;
нельзя представить пятой степенью натурального числа; 
 – промежуточное значение между
– промежуточное значение между  и
и  , между
, между  и
и  , между
, между  и
и  ; Проверим далее:
; Проверим далее:
 нельзя представить как “
нельзя представить как “ ”, (
”, (
– также нельзя представить как “ ”
”
Другие примеры также подтверждают, что сумму “ ”, – можно представить только как “
”, – можно представить только как “ ”, где
”, где  – число, которое не образуется пятой степенью натурального числе (“
– число, которое не образуется пятой степенью натурального числе (“ ”).
”).
“ ” компактное отображение ряда Тейлора, разложения функции (линейной) в бесконечную сумму степенных функций, условно от “
” компактное отображение ряда Тейлора, разложения функции (линейной) в бесконечную сумму степенных функций, условно от “ ” к “
” к “ ”, и далее к “
”, и далее к “ ”.
”.
Функция “ ” может рассматриваться как “Свёртка”, модифицированная версия одной из “
” может рассматриваться как “Свёртка”, модифицированная версия одной из “ ” или “
” или “ ”… Если рассмотреть
”… Если рассмотреть  как компактную топологическую группу, сумму “
как компактную топологическую группу, сумму “ ” представить как “
” представить как “ ”, “
”, “ ” как “
” как “ ”, то используя левую меру Хаара ϻ (определена на Ϭ-кольце), порождённом всеми компактными множествами, и не равную тождественно нулю, конечную на компактных множествах, получим:
”, то используя левую меру Хаара ϻ (определена на Ϭ-кольце), порождённом всеми компактными множествами, и не равную тождественно нулю, конечную на компактных множествах, получим:
, для любых  (локально компактная топологическая группа); E – область определения ϻ (степенных значений).
(локально компактная топологическая группа); E – область определения ϻ (степенных значений).
Вывод: левая мера Хаара, образование степенных функций из линейных (ряд Тейлора), о чём говорит значение  в
в  (
( не есть
не есть  ; все числа натуральные) указывают на невозможность выполнения равенства
; все числа натуральные) указывают на невозможность выполнения равенства
 (
( )
)
Литература:
В.А. Зорич Математический анализ






 такие, что
такие, что  ?
? образующие
образующие  , то убрав везде “
, то убрав везде “ ”, получим:
”, получим: 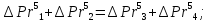





 ” возможно при изначально, вдвое большей суммы “
” возможно при изначально, вдвое большей суммы “ ”, чем в условии задачи, то есть равенство
”, чем в условии задачи, то есть равенство  ;
; 
 и
и  есть общее
есть общее 

 совпадает с
совпадает с 










