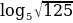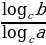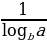СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока





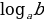 = х
= х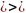 a х = b
a х = b 0, b
0, b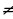 1)
1)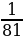 = – 4, т. к. 3- 4 =
= – 4, т. к. 3- 4 =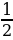 1
1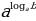 = b
= b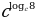 = 8
= 8 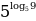 = 9
= 9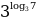
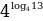
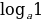 = 0
= 0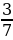 1 = 0 (т. к.
1 = 0 (т. к. 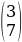 0 = 1)
0 = 1)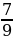 1
1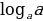 = 1
= 1 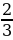
 y) = loga x + loga y
y) = loga x + loga y 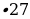 ) = log3 9 + log3 27 = 2+3 = 5
) = log3 9 + log3 27 = 2+3 = 5 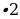 ) = log4 16 = 2
) = log4 16 = 2 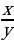 = loga x – loga y
= loga x – loga y 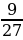 = log3 9 – log3 27 = 2 – 3 = –1 2) log4 8 – log4 2 = log4
= log3 9 – log3 27 = 2 – 3 = –1 2) log4 8 – log4 2 = log4 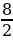 = log4 4 = 1
= log4 4 = 1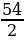
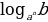 =
= 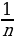 · loga b
· loga b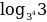 =
= 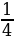 · log3 3 =
· log3 3 = 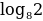
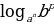 =
= 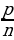 · loga b
· loga b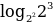 =
= 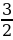 · log2 2 = 1,5 ·1 = 1,5
· log2 2 = 1,5 ·1 = 1,5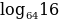
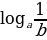 = –
= – 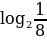 = –
= – 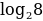 = – 3
= – 3 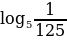
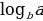 = 1
= 1 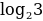 ·
· 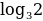 = 1
= 1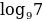 ·
· 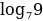
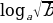 =
= 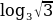 =
= 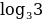 =
=