Сызыктуу теңдемелер системасы

Токтогул атындагы №1 мектеп-гимназиясынын математика мугалими Кырбашова Бүбүайша Асековнанын 7-класстар үчүн өтүлгөн сабагы

Эки белгисиздүү теңдемелердин системасы

• Ар кандай сандар, ал эми
• х жана у – белгисиз сандар

Эки белгисиздүү теңдемелердин системасы

АНЫКТАМА:

Эки белгисизи бар теңдемелердин системасынын тамыры деп, системанын ар бир теңдемесин туура барабардыкка айландыруучу белгисиздердин түгөй маанилерин айтабыз.

Жалпы түрүндө ал төмөнкүчө жазылат :

а 1 х + b 1 y = c 1,

а 2 х + b 2 y = c 2 ;

а 1 , b 1 , c 1 ,

а 2 , b 2 , c 2

Мында,

ах + b у = с теңдемесин мүнөздө а, b, с лар кайсылар? Таблицаны толтургула:

ах + b у = с

а

6х – 2у = - 5

b

Х + 0,5 у = 0

с

0,75х – у = 1

- 0,25х + у = 1,5

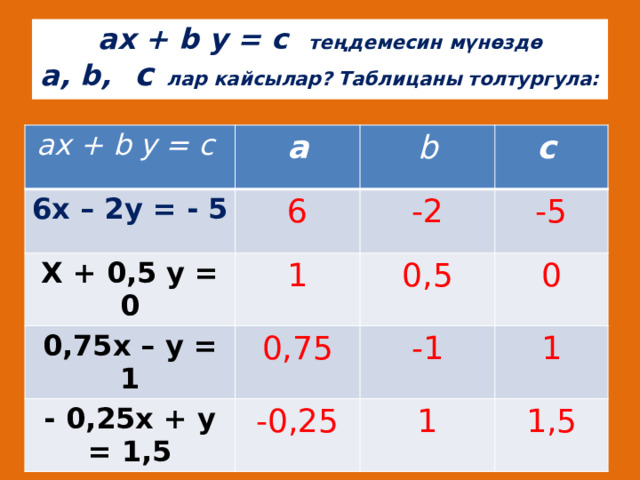
ах + b у = с теңдемесин мүнөздө а, b, с лар кайсылар? Таблицаны толтургула:

ах + b у = с

а

6х – 2у = - 5

6

Х + 0,5 у = 0

b

0,75х – у = 1

1

-2

с

-5

0,75

0,5

- 0,25х + у = 1,5

0

-1

-0,25

1

1

1,5

Теңдемелер системасынын чыгаруу жолдору

а₁ х + b₁ y = c₁,

а ₂ х + b₂ y = c₂ ;

мында а₁ , b₁ , c₁

х , у –белгисиз сандар

а₂ , b₂ , c₂ –ар кандай сандар

График аркылуу чыгаруу жолу

Ордуна коюу жолу

Коэффициенттерин теңдеп алып кошуу жолу

Теңдемелер системасын график аркылуу чыгаруу

• Максаты : Эки белгисиздүү сызыктуу теңдемелерди график аркылуу чыгаруу жолу менен таанышат..

а₁ х + b ₁ y= c₁

a₂ х + b₂ y = c₂

М

y

• Графиктик жол адатта чыгарылышты жакындатып гана табууга мүмкүндүк берет.
• Системанын теңдемелеринин графиктери түз сызык болот.

у

х

x

Теңдемелер системасын график аркылуу чыгарабыз

у ти х аркылуу

туюнтабыз

у - х=2,

у+х=10;

y

y=x+2

●

10

у=2+х,

у=10-х;

Биринчи теңдемеге

график түзөбүз

6

у=2+х

y=10 - x

х

0

-2

х

0

-2

у

●

у

2

2

0

1

Экинчи теңдемеге

график түзөбүз

●

●

x

10

1

4

-2

0

0

у=10 - х

х

х

10

0

0

10

Жообу: (4; 6)

у

у

10

0

М

М

М

Теңдемелер системасынын графиктерин чыгарууда үч негизге токтолобуз. Алардын графиктери түз сызыктар болушат.

Кесилишкен түз сызыктар

Дал келген түз сызыктар

Параллель түз сызыктар

y

y

y

x

x

x

Эгерде түз сызыктар кесилишсе жалгыз гана чыгарылышка ээ болушат

Эгерде ушул түз сызыктар параллель болушса, анда система чыгарылышка ээ болбойт;

эгерде түз сызыктар дал келип калышса, анда системанын чыгарылыштары чексиз болот

Үч касиет боюнча төмөнкүлөрдүн жоопторун тапкыла

М

М

• № 1

1). Сызыктардын салыштырмалуу абалын көрсөтүңүз :

2х – у = 4 жана 3х – у = 6.

А). кесилишет;

Б). Дал келет;

В). параллель.

2).Чиймеден теңдемелер системасынын жоопторун тапкыла.

№ 2

1). Сызыктардын салыштырмалуу абалын көрсөтүңүз :

2х – у = 3 жана х – у = 2.

А). кесилишет;

Б). Дал келет;

В). параллель.

2).Чиймеден теңдемелер системасынын жоопторун тапкыла.

А)

y

y

Х+ 2у =4,

А)

Х- 2у =1,

2х- у = 5;

2х+у= 4;

Б)

2у+ х =5,

2х+2у= 6;

Б)

2Х - 3у =7,

3х - 2у= 8;

2

2

x

1

x

1

В)

2Х+ у =5,

0

2х+у= 4;

1

3

В)

Х+ у =5,

У = 5 - х;

Үйгө тапшырма

№ 1124;

№ 1125

К онул бурганынарга

рахмат !