Решение иррациональных уравнений
Иррациональные уравнения
Уравнения, в которых под знаком корня содержится переменная, называют иррациональными.
Методы решения иррациональных уравнений, как правило, основаны на возможности замены (с помощью некоторых преобразований) иррационального уравнения рациональным уравнением, которое либо эквивалентно исходному иррациональному уравнению, либо является его следствием. Чаще всего обе части уравнения возводят в одну и ту же степень. При этом получается уравнение, являющееся следствием исходного.
При решении иррациональных уравнений необходимо учитывать следующее:
1) если показатель корня - четное число, то подкоренное выражение должно быть неотрицательно; при этом значение корня также является неотрицательным (определение корня с четным показателем степени);
2) если показатель корня - нечетное число, то подкоренное выражение может быть любым действительным числом; в этом случае знак корня совпадает со знаком подкоренного выражения.
Существует несколько подходов в решению иррациональных уравнений. Рассмотрим наиболее распространенные:
замена исходного уравнения равносильным ему уравнением (системой или совокупностью уравнений и неравенств);
замена исходного уравнения его следствием.
Способ 1. Замена исходного уравнения равносильным ему уравнением (системой или совокупностью уравнений и неравенств)
Поскольку все равносильные уравнения имеют одни и те же решения, то при этом подходе проверка полученных значений переменной по условию исходного уравнения не является необходимой частью решения.
При решении иррациональных уравнений часто пользуются следующими утверждениями о равносильности:


Способ 2. Замена исходного уравнения его следствием.
Поскольку решений в уравнении-следствии (системе, совокупности) может быть больше, чем в исходном уравнении, то необходимо выполнить проверку полученных значений переменной по условию исходного уравнения.
Переход к следствию из данного уравнения при оформлении записи решения можно обозначать символом 
Пример 1. Решить уравнение  .
.
Решение.
Возведем обе части уравнения в квадрат.





Произведем проверку полученных корней, для этого произведем подстановку значений переменной x в исходное уравнение.
Проверка.
При x1 = -2  - истинно.
- истинно.
При x2 = 2  - истинно.
- истинно.
Отсюда следует, что исходное иррациональное уравнение имеет два корня -2 и 2.
Ответ: -2 и 2.
Пример 2. Решить уравнение  .
.
Это уравнение можно решить по такой же методике как и в первом примере, но мы поступим иначе.
Найдем ОДЗ данного уравнения. Из определения квадратного корня следует, что в данном уравнении одновременно должны выполнятся два условия:
а) x - 9  0;
0;
x  9;
9;
б) 1 - x  0;
0;
-x  -1 ;
-1 ;
x  1.
1.
ОДЗ данного ураdнения: x
 .
.
Ответ: корней нет.
Пример 3.
Решить уравнение 
Решение.
Нахождение ОДЗ в этом уравнении представляет собой достаточно трудную задачу. Возведем обе части уравнения в квадрат:








Произведя проверку устанавливаем, что x2=0 лишний корень.
Ответ: x=1.
Пример 4. Решить уравнение x =  .
.
Решение.
В этом примере ОДЗ найти легко. ОДЗ этого уравнения: x [-1;
[-1;  ).
).
Возведем обе части этого уравнения в квадрат, в результате получим уравнение x2= x + 1. Корни этого уравнения:
x1 = 
x2 = 
Произвести проверку найденных корней трудно. Но, несмотря на то, что оба корня принадлежат ОДЗ утверждать, что оба корня являются корнями исходного уравнения нельзя. Это приведет к ошибке. В данном случае иррациональное уравнение равносильно совокупности двух неравенств и одного уравнения:
x + 1  0 и x
0 и x  0 и x2 = x + 1, из которой следует, что отрицательный корень для иррационального уравнения является посторонним и его нужно отбросить.
0 и x2 = x + 1, из которой следует, что отрицательный корень для иррационального уравнения является посторонним и его нужно отбросить.
Ответ: 
Пример 5 . Решить уравнение  +
+  = 7.
= 7.
Решение.
Возведем обе части уравнения в квадрат и выполним приведение подобных членов, перенес слагаемых из одной части равенства в другую и умножение обеих частей на 0,5. В результате мы получим уравнение


 = 12, (*) являющееся следствием исходного. Снова возведем обе части уравнения в квадрат. Получим уравнение (х + 5)(20 - х) = 144, являющееся следствием исходного. Полученное уравнение приводится к виду x2 - 15x + 44 =0.
= 12, (*) являющееся следствием исходного. Снова возведем обе части уравнения в квадрат. Получим уравнение (х + 5)(20 - х) = 144, являющееся следствием исходного. Полученное уравнение приводится к виду x2 - 15x + 44 =0.
Это уравнение (также являющееся следствием исходного) имеет корни x1 = 4, х2= 11. Оба корня, как показывает проверка, удовлетворяют исходному уравнению.
Ответ: х1 = 4, х2= 11.
Замечание. При возведении уравнений в квадрат учащиеся нередко в уравнениях типа (*) производят перемножение подкоренных выражений, т. е. вместо уравнения •
• = 12, пишут уравнение
= 12, пишут уравнение  = 12. Это не приводит к ошибкам, поскольку уравнения являются следствиями уравнений. Следует, однако, иметь в виду, что в общем случае такое перемножение подкоренных выражений дает неравносильные уравнения.
= 12. Это не приводит к ошибкам, поскольку уравнения являются следствиями уравнений. Следует, однако, иметь в виду, что в общем случае такое перемножение подкоренных выражений дает неравносильные уравнения.
В рассмотренных выше примерах можно было сначала перенести один из радикалов в правую часть уравнения. Тогда в левой части уравнения останется один радикал и после возведения обеих частей уравнения в квадрат в левой части уравнения получится рациональная функция. Такой прием (уединение радикала) довольно часто применяется при решении иррациональных уравнений.
Пример 6. Решить уравнение  -
-  = 3.
= 3.
Решение.
Уединив первый радикал, получаем уравнение
 =
=  + 3, равносильное исходному.
+ 3, равносильное исходному.
Возводя обе части этого уравнения в квадрат, получаем уравнение
x2 + 5x + 2 = x2 - 3x + 3 + 6 ,
,
равносильное уравнению
4x - 5 = 3 (*).
(*).
Это уравнение является следствием исходного уравнения. Возводя обе части уравнения в квадрат, приходим к уравнению
16x2 - 40x + 25 = 9(x2 - 3х + 3), или
7x2 - 13x - 2 = 0.
Это уравнение является следствием уравнения (*) (а значит, и исходного уравнения) и имеет корни. Первый корень x1 = 2 удовлетворяет исходному уравнению, а второй x2 =  - не удовлетворяет.
- не удовлетворяет.
Ответ: x = 2.
Заметим, что если бы мы сразу, не уединив один из радикалов, возводили обе части исходного уравнения в квадрат нам бы пришлось выполнить довольно громоздкие преобразования.
При решении иррациональных уравнений, кроме уединения радикалов используют и другие методы. Рассмотрим пример использования метода замены неизвестного (метод введения вспомогательной переменной).
Пример 7. Решить уравнение 2x2 - 6x +  + 2 = 0.
+ 2 = 0.
Решение.
Введем вспомогательную переменную. Пусть y =  , где y
, где y  0, тогда получим уравнение 2y2 + y - 10 = 0; y1 = 2; y2 = -
0, тогда получим уравнение 2y2 + y - 10 = 0; y1 = 2; y2 = -  .
.
Второй корень не удовлетворяет условию y  0.
0.
Возвращаемся к x:
 = 2;
= 2;
x2 - 3x + 6 = 4;
x2 -3x + 2 = 0;
x1 = 1; x2 = 2.
Проверкой устанавливаем, что оба корня являются корнями исходного уравнения.
Ответ: x1 = 1; x2 = 2.
Пример 8. Решить уравнение  +
+  =
= 
Решение.
Положим  = t, Тогда уравнение примет вид t +
= t, Тогда уравнение примет вид t +  =
=  откуда получаем следствие: 2t2 - 5t + 2 = 0.
откуда получаем следствие: 2t2 - 5t + 2 = 0.
Решая это квадратное уравнение, находим два корня: t1 = 2 t2 =  .
.
Задача сводится теперь к решению следующих двух уравнений:
 = 2, (*)
= 2, (*)  =
=  (**)
(**)
Возводя обе части уравнения (*) в куб, получаем 12 - 2x = 8x - 8; x1 = 2.
Аналогично, решив (**), находим x2 =  .
.
Оба найденных корня удовлетворяют исходному уравнению, так как в процессе решения мы использовали (кроме замены неизвестного) только преобразование вида [f(x) = g(x)]  [fn(x) = gn(x)], а при таком преобразовании, как было отмечено выше, получается равносильное уравнение.
[fn(x) = gn(x)], а при таком преобразовании, как было отмечено выше, получается равносильное уравнение.
Ответ: х1 = 2, x2 =  .
.
Пример. Решить уравнение 
Решение. Возведем обе части уравнения в квадрат:
Приводим подобные. При этом в левой части уравнения записываем корень, остальные слагаемые – в правой части:

Возводим полученное уравнение в квадрат еще раз:
Решая последнее квадратное уравнение, находим корни 
 которые теперь необходимо проверить. Делаем проверку корней подстановкой в исходное уравнение. Первый корень не подходит.
которые теперь необходимо проверить. Делаем проверку корней подстановкой в исходное уравнение. Первый корень не подходит.
Приходим к ответу: 
Пример. Решить уравнение 
Решение. Возведем обе части уравнения в куб:
Воспользовавшись исходным уравнением, заменим выражение  выражением
выражением  Получаем:
Получаем:
Решаем совокупность уравнений
В результате замены выражения могут появиться посторонние корни, так как такое преобразование не является равносильным. Поэтому необходимо произвести проверку. Подставляем найденные значения и убеждаемся, что они являются корнями исходного уравнения.
Приходим к ответу: 
Пример. Решить уравнение 
Решение. Возведение уравнения в квадрат приводит к уравнению четвертой степени и громоздкому решению.
Нетрудно заметить, что в данном уравнении можно произвести замену. Но перед этим преобразуем уравнение следующим образом:
Заменив  получаем квадратное уравнение
получаем квадратное уравнение

Решая его, находим корни 
Возвращаемся к исходной неизвестной:
Первое уравнение решений не имеет, так как его левая часть неотрицательна, а правая – отрицательна. Второе уравнение возводим в квадрат. Получаем:
 т. е.
т. е. 
Его корни  С помощью проверки убеждаемся, что оба корня подходят, т. е. приходим к ответу:
С помощью проверки убеждаемся, что оба корня подходят, т. е. приходим к ответу: 
Пример. Решить уравнение 
Решение.
1-й способ. Перенесем второй корень вправо:

Возводим обе части в квадрат:
Еще раз возводим в квадрат и получаем квадратное уравнение, решая которое и получаем корни  Делаем проверку корней подстановкой в исходное уравнение. Оба корня подходят.
Делаем проверку корней подстановкой в исходное уравнение. Оба корня подходят.
2-й способ. Введем замену  тогда
тогда 
 Таким образом получили более простое уравнение
Таким образом получили более простое уравнение
 т. е.
т. е. 
Возведем его в квадрат:
Возвращаемся к исходной неизвестной:

Возводим обе части уравнения в квадрат:
 откуда
откуда 
При помощи проверки убеждаемся, что оба корня подходят.
3-й способ. Домножим обе части уравнения на выражение, сопряженное левой части исходного уравнения. Получим:
Сложим последнее уравнение с исходным. Получим:
 т. е.
т. е. 
Последнее уравнение возводим в квадрат. Получаем квадратное уравнение

Решая его, находим корни 
Приходим к ответу: 
Пример. Решить уравнение 
Решение. Пусть  Тогда
Тогда  и
и 
 по условию.
по условию.
Получили систему
Решаем ее методом подстановки:
Второе уравнение решим отдельно
Получаем корни:

Возвращаемся к системе:
Получаем:
Переходим к заданным неизвестным:
Решая последнюю совокупность, находим корни  и
и  С помощью проверки убеждаемся, что оба корня подходят.
С помощью проверки убеждаемся, что оба корня подходят.
Получили ответ: 

При решении иррациональных уравнений, как правило, нахождение ОДЗ является бесполезным, так как проверка решений по ОДЗ недостаточна. Но существует ряд примеров, в которых нахождение ОДЗ является тем методом, который приводит к успеху. Покажем это на следующем примере.
Пример. Решить уравнение

Решение. Найдем ОДЗ данного уравнения:
Решаем последнюю систему неравенств графически (рис. 10).

Рис. 10
Получили, что ОДЗ состоит из единственной точки 
Остается подставить значение  в уравнение и выяснить, является ли оно решением:
в уравнение и выяснить, является ли оно решением:

Получили, что  – решение.
– решение.
Пример. Решить уравнение 
Решение. Используем графический способ. Строим графики функций 
 (рис.11).
(рис.11).
Рис. 11
Из рисунка видно, что графики пересекаются в единственной точке x = 7. Следовательно, уравнение имеет единственное решение. Проверяем x = 7 подстановкой в заданное уравнение и убеждаемся, что это точное значение решения уравнения.
Получили ответ: x = 7.
Задания
I уровень
1.1. Определите, имеет ли уравнение корни:
1)  2)
2)  3)
3)  4)
4) 
5)  6)
6)  7)
7)  8)
8) 
9)  10)
10) 
1.2. Решите уравнение:
1)  2)
2)  3)
3) 
4)  5)
5)  6)
6) 
7)  8)
8)  9)
9) 
10)  11)
11)  12)
12) 
13)  14)
14)  15)
15) 
16)  17)
17)  18)
18) 
19)  20)
20)
21)  22)
22) 
1.3. Решите уравнение:
1)  2)
2) 
3)  4)
4) 
5)  6)
6) 
7)  8)
8) 
9)  10)
10) 
1.4. Решите уравнение графически:
1)  2)
2) 
3)  4)
4) 
II уровень
2.1. Решите уравнение:
1)
2) 
3)
4)
5)
6)
7) 
8) 
9) 
10)
11)
12) 
13)
14)
15) 
16)
III уровень
3.1. Решите уравнение:
1)
2)
3)
4)
5) 
6)
7)
8)
9)
3.2. Решите уравнение:
1)  2)
2) 







 , где
, где 
 .
. .
.



 не определено, в случае
не определено, в случае  . Если
. Если 







 имеет два решения
имеет два решения  . Это числа, квадрат которых равен 4.
. Это числа, квадрат которых равен 4. . Нарисуем график функции
. Нарисуем график функции  и увидим, что и у этого уравнения два решения, одно положительное, другое отрицательное.
и увидим, что и у этого уравнения два решения, одно положительное, другое отрицательное.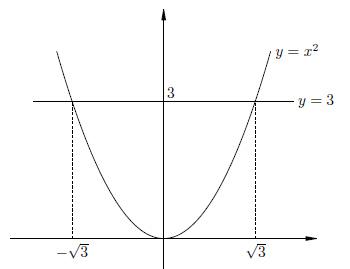
 — это неотрицательное число, квадрат которого равен
— это неотрицательное число, квадрат которого равен  .
.  — выражение
— выражение  .
.
 .
. 
 .
. , то неотрицательный корень уравнения
, то неотрицательный корень уравнения  называется арифметическим корнем
называется арифметическим корнем 

 называют еще радикалом.
называют еще радикалом.
 не являются рациональными числами.
не являются рациональными числами.
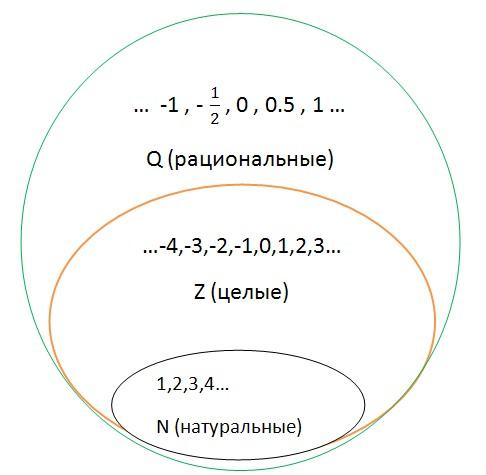
 , где
, где 
 .
. , так как
, так как  .
. ;
;  .
. (обозначается
(обозначается  ) называется положительный корень
) называется положительный корень  .
.
 .
. не имеют смысла.
не имеют смысла. и т.д.
и т.д.









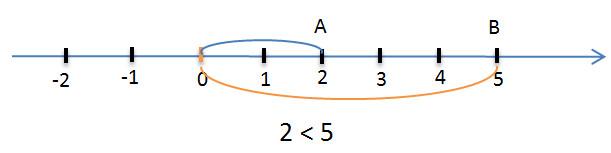
 и целом
и целом 
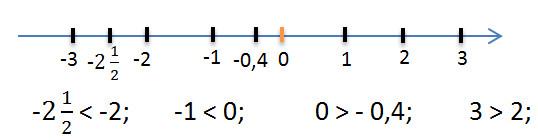
 . Тогда
. Тогда 
 , то
, то 
 . Тогда
. Тогда 

 и т. д.
и т. д.  , где
, где 
 .
. – четное натуральное число.
– четное натуральное число. , где n - натуральное число, обладает следующими свойствами:
, где n - натуральное число, обладает следующими свойствами: ;
; ;
; четная, так как
четная, так как  ;
;  и возрастающей на промежутке
и возрастающей на промежутке  .
. рафик функции
рафик функции 


 –
–  , где
, где ;
; нечетная, так как
нечетная, так как  ;
; рафик функции
рафик функции 









 .
. 




 - истинно
- истинно - истинно.
- истинно. .
.



















 и
и  , значит в силу транзитивного свойства неравенств, всюду, где выполняются указанные неравенства,
, значит в силу транзитивного свойства неравенств, всюду, где выполняются указанные неравенства,  и поэтому систему можно заменить другой системой
и поэтому систему можно заменить другой системой 
 .
.





 имеет положительный старший коэффициент и отрицательный дискриминант, следовательно, он принимает только положительные значение, а это значит, что неравенство
имеет положительный старший коэффициент и отрицательный дискриминант, следовательно, он принимает только положительные значение, а это значит, что неравенство  решений не имеет.
решений не имеет. 




 a = 1 и D = -39, следовательно, он принимает положительные значения на всей области определения.
a = 1 и D = -39, следовательно, он принимает положительные значения на всей области определения.
 .
.


 следует, что
следует, что  .
. .
. 
 совпадает со знаком выражения
совпадает со знаком выражения 



 .
. .
.









