МУНИЦИПАЛЬНОЕ КАЗЕННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №1 ИМЕНИ ГЕРОЯ СОЦИАЛИСТИЧЕСКОГО ТРУДА ЕРУСЛАНА ЕЛАМУРЗАЕВИЧА ДЗГОЕВА С.ЭЛЬХОТОВО МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ КИРОВСКИЙ РАЙОН РЕСПУБЛИКИ СЕВЕРНАЯ ОСЕТИЯ-АЛАНИЯ
Открытый урок
по теме: «Приведенное квадратное уравнение»
в 8 «А» классе
Учитель математики: Бетеева З.С.
2021-2022 уч.г
Тема: «Приведенное квадратное уравнение»
Цель урока:
Ввести понятие приведенного квадратного уравнения,
Вывести формулу корней приведенного квадратного уравнения,
Научить учащихся решать приведенные квадратные уравнения, пользуясь формулой с четным вторым коэффициентом.
Тип урока: урок ознакомления с новым материалом.
План урока.
| № | Этап урока | Содержание (цель)этапа | Время (мин) |
| 1 | Организационный момент | Постановка цели урока. Создание благоприятных условий для успешной деятельности. Мотивация учения. | 1 |
| 2 | Проверка домашнего задания | Фронтальная, индивидуальная проверка | 2 |
| 3 | Устные упражнения | Коррекция знаний и умений учащихся. | 3 |
| 4 | Изучение нового материала | Формирование опорных знаний, формулировка правил, решение задач, анализ результатов, ответы на вопросы учащихся. | 10 |
| 5 | Закрепление изученного материала | Усвоение изученного материала путем его применения при решении задач по аналогии под контролем учителя. | 10 |
| 6 | Работа в парах | Проверка знаний и умений | 3 |
| 7 | Историческая справка | Сведения о Виете | 2 |
| 8 | Самостоятельная работа | Проверка степени усвоения учащимися изученного материала. | 5 |
| 9 | Подведение итогов урока | Оценка знаний отвечавших учеников. Проверка знаний и понимания формулировок правил методом фронтального опроса. | 2 |
| 10 | Домашнее задание | Ознакомление учащихся с содержанием задания и получение необходимых пояснений. | 2 |
Если ты услышишь, что кто-то не любит
математику, не верь. Её нельзя не любить –
её можно только не знать.
Ход урока.
Организационный момент. Постановка цели урока. Создание благоприятных условий для успешной деятельности. Мотивация учения.
II. Проверка домашнего задания. Фронтальная, индивидуальная проверка и коррекция знаний и умений учащихся.
На предыдущих уроках мы работали над темой «Квадратные уравнения». Изучили решение квадратных уравнений с помощью выделения квадрата двучлена, раскладывать на линейные множители, распознавать полные квадратные уравнения от неполных, с помощью формул учились находить корни уравнения.
Начнем с проверки домашнего задания и повторения основного теоретического материала, необходимого для изучения новой темы.
Дома учащиеся должны были заполнить таблицу. Эта таблица изображена на доске. К доске вызывается один ученик с тетрадью и заполняет таблицу.
В это время проводится фронтальный опрос по следующим вопросам:
1.Сформулируйте определение квадратного уравнения.
2.Какое уравнение называется неполным квадратным уравнением?
3.Какое уравнение называют приведенным квадратным уравнением?
4.Что называют дискриминантом квадратного уравнения?
5.Сколько корней может иметь квадратное уравнение и отчего это зависит?
После опроса проверяется таблица, заполненная на доске.
| № | Уравнение | а | b | c | 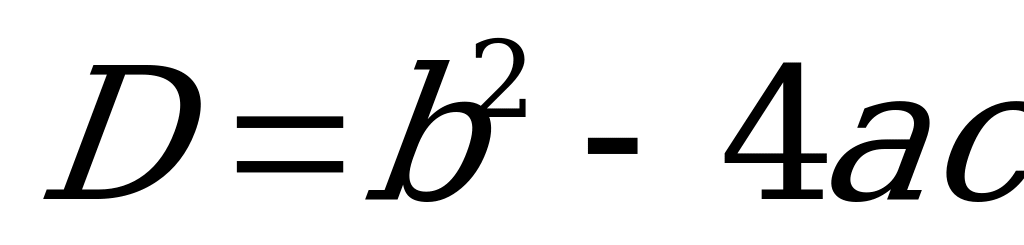
| Количество корней |
| 1 | 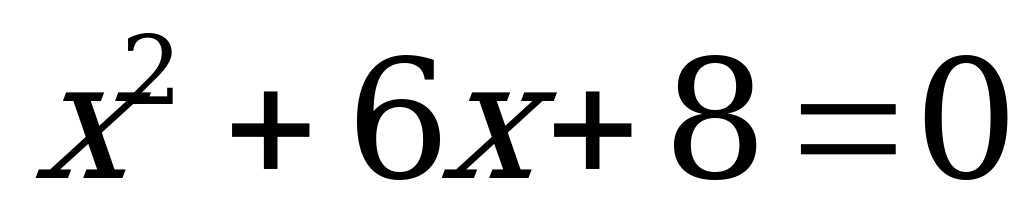
|
|
|
|
|
|
| 2 | 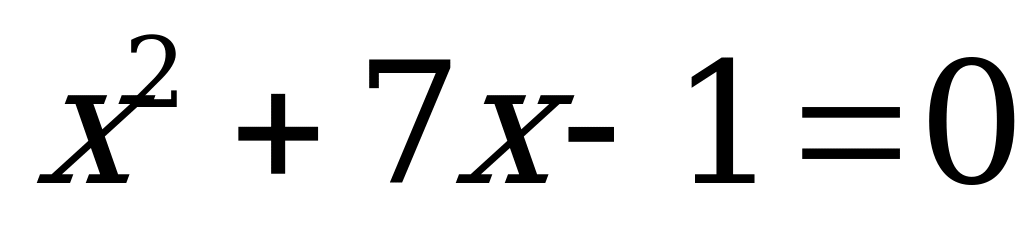
|
|
|
|
|
|
| 3 | 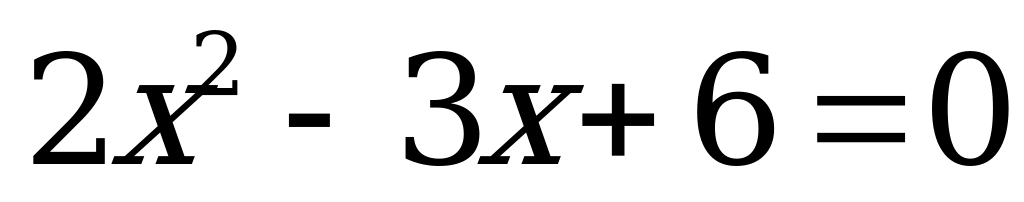
|
|
|
|
|
|
| 4 | 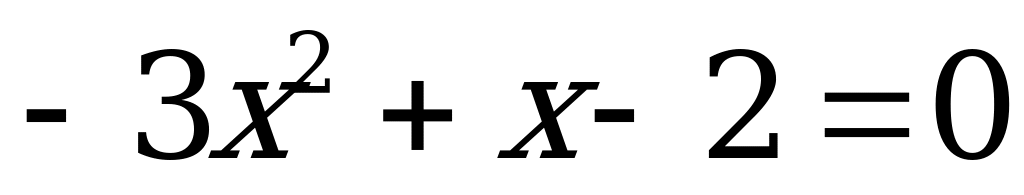
|
|
|
|
|
|
| 5 | 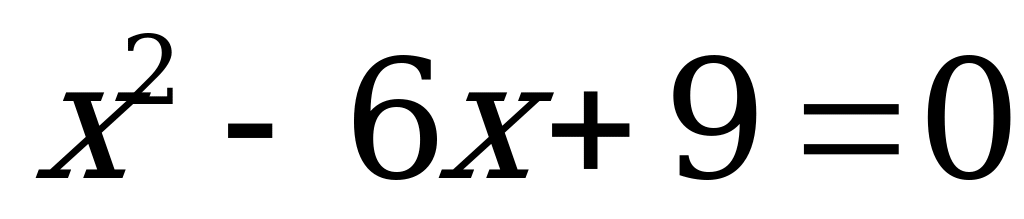
|
|
|
|
|
|
| 6 | 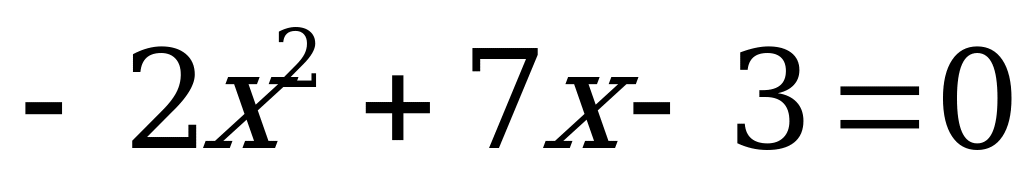
|
|
|
|
|
|
Работа по карточкам. Три ученика вызываются к доске.
Вычислите дискриминант квадратного трехчлена: х2 – 14х + 49
Выделите полный квадрат: х2 + 8х + 12
3. Разложите квадратный трехчлен на линейные множители: х2 + 5х – 6
III. Актуализация знаний.
Устная работа
1. Назовите виды уравнений, записанных на доске.
2x2 + 6x + 5 = 0
x2-7x +10 = 0
3x2 - 25x + 28 = 0
2x2 + 4x = 0
4x2 – 25 = 0
x2 – 64 = 0
2. Назовите из них неполные квадратные уравнения;
3.Назовите из них приведенное квадратное уравнение.
IV. Изучение нового материала.
Учитель предлагает в известном виде квадратного трехчлена ax2 +bx+c заменить a=1, b=q, c=p.
Выйти к доске, записать получившийся квадратный трехчлен x2 +px+q. Записать, как будет выглядеть дискриминант, выраженный через буквы p, q.
D=p2 – 4q.
Разобрать пример с учебника
V.Закрепление изученного материала
№ 257 (1 ст)
№ 258 (1 ст)
VI. Работа в парах. Реши уравнения:
| № | Уравнение | Корни уравнения |
| 1. | х2 + х –12 = 0 | 3 и -4 |
| 2. | х2 - 12х – 45 = 0 | -3 и 15 |
| 3. | у2+ 8у +15 = 0 | -3 и -5 |
| 4. | у2- 5у +6 = 0 | 2 и 3 |
| 5. | z2-10z +21 = 0 | 3 и 7 |
| 6. | z2- 3z -10 = 0 | -2 и 5 |
VII. Историческая справка
Впервые зависимость между корнями и коэффициентами квадратного уравнения установил знаменитый французский ученый Франсуа Виет (1540–1603).
Франсуа Виет был по профессии адвокатом и много лет работал советником короля. И хотя математика была его увлечением, или как говорят хобби, благодаря упорному труду он добился в ней больших результатов. Виет в 1591 г. ввел буквенное обозначения для неизвестных и коэффициентов уравнений. Что дало возможность записывать общими формулами корни и другие свойства уравнения.
Недостатком алгебры Виета было то, что он признавал только положительные числа. Чтобы избежать отрицательных решений, он заменял уравнения или искал искусственные приемы решения, что отнимало много времени, усложняло решение и часто приводило к ошибкам.
Много разных открытий сделал Виет, но сам он больше всего дорожил установлением зависимости между корнями и коэффициентами квадратного уравнения, то есть той зависимостью, которая называется “теоремой Виета”.
Эту теорему мы будем рассматривать на следующем уроке.
VIII. Самостоятельная работа по вариантам
Вариант 1
x2 – 5x + 6 = 0;
x2 + 8x + 15 = 0;
Вариант 2
х2 – 6х + 8 = 0;
х2 – 2х – 15 = 0;
Вариант 3
х2 – 4х + 4 = 0;
х2 + 4х + 3 = 0;
IX.Подведение итогов урока.
Ответьте на вопросы:
Какие уравнения называются приведенными?
Можно ли обычное квадратное уравнение сделать приведенным?
Рефлексия
На уроке я успел сделать…
В результате я узнал и научился…
Я не понял, у меня не получилось…
Оценки.
X. Домашнее задание.
П.4.4 №№ 255, 256(устно),
№ 258 (2 ст)
№ 254 (б,г)
















