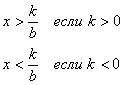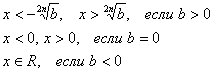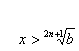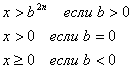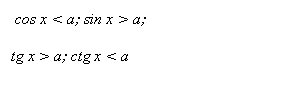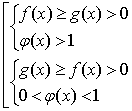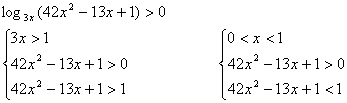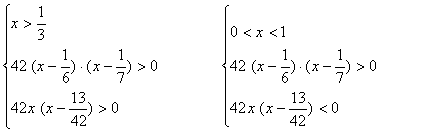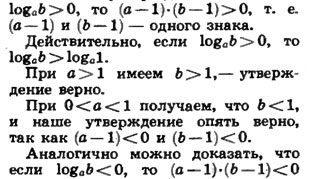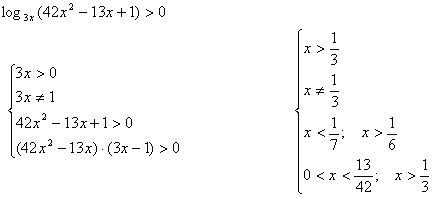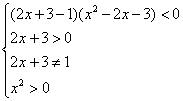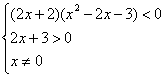План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока: Понятие неравенство. Решение неравенства.
1. Виды неравенств и их решение.
|
Вид неравенства
|
Решение
|
|
Линейные

|

|
|
Содержащие чётную степень

|

|
|
Содержащие нечётную степень

|

|
|
Иррациональные

|

|
|
Иррациональные

|

|
|
Показательные
 
|


|
|
Логарифмические


|
 
|
|
Тригонометрические

|
При решении используют тригонометрическую окружность или график соответствующей функции
|
2. Равносильность неравенств.
Перечислим некоторые преобразования неравенств, приводящие данное неравенство к неравенству, равносильному ему на множестве всех действительных чисел.
- Перенос члена неравенства (с противоположным знаком) из одной части неравенства в другую;
- Умножение (деление) обеих частей неравенства на положительное число;
- Применение правил умножения многочленов и формул сокращённого умножения;
- Приведение подобных членов многочлена;
- Возведение неравенства в нечётную степень;
- Логарифмирование неравенства
 , т.е замена этого неравенства неравенством
, т.е замена этого неравенства неравенством
Назовем преобразования неравенств, приводящие исходное неравенство к неравенству равносильному ему на некотором множестве чисел
- Возведение неравенства в чётную степень; (на множестве где обе функции неотрицательны)
- Потенцирование неравенства; (на множестве где обе функции положительны)
- Умножение обеих частей неравенства на функцию; (на множестве где функция положительна)
- Применение некоторых формул (логарифмических, тригонометрических и др.) (на множестве где одновременно определены обе части применяемой формулы)
В зависимости от интерпретации неравенства различают
- алгебраический
- функциональный
- графический
- геометрический.
Среди алгебраических методов решения неравенств выделяют:
- Сведение неравенства к равносильной системе или совокупности систем
- Метод замены
- Разбиение области определения неравенства на подмножества
Логарифмическое неравенство  можно свести к равносильной совокупности систем неравенств
можно свести к равносильной совокупности систем неравенств

Решите неравенство:




Ответ: 
Оказывается, что данное неравенство можно решить иначе.
Зная свойства логарифма о том, что logа b < 0, если a и b по разные стороны от 1, log a b > 0, если a и b по одну сторону от 1, можно получить очень интересный и неожиданный способ решения неравенства. Об этом способе написано в статье “Некоторые полезные логарифмические соотношения” в журнале “Квант” № 10 за 1990 год.

Решите это неравенство, используя новые соотношения

Ответ: 
Оказывается, что при решении некоторых логарифмических неравенств можно использовать и другие соотношения
развернуть таблицу
|
Заменяемое выражение
|
Используемое выражение
|
|

|

|
|

|

|
|

|

|
|

|

|
|

|

|
|

|

|
развернуть таблицу
Решите неравенство 
у доски составляем систему, которую решают самостоятельно





Просмотр содержимого документа
«Тема урока: Понятие неравенство. Решение неравенства.»
План урока
Курс__, гр__
Дисциплина: Математика
Профессия: Пчеловод
Преподаватель:
Тема урока: Понятие неравенство. Решение неравенства.
1. Виды неравенств и их решение.
| Вид неравенства | Решение |
| Линейные
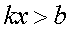 | 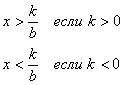
|
| Содержащие чётную степень
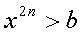 | 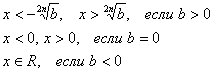
|
| Содержащие нечётную степень
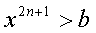 | 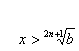
|
| Иррациональные
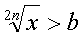 | 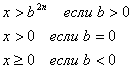
|
| Иррациональные
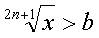 | 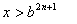
|
| Показательные
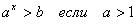 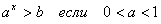 | 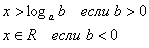
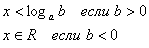
|
| Логарифмические
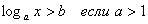
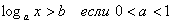 | 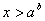 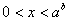
|
| Тригонометрические
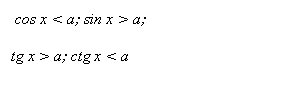 | При решении используют тригонометрическую окружность или график соответствующей функции |
2. Равносильность неравенств.
Перечислим некоторые преобразования неравенств, приводящие данное неравенство к неравенству, равносильному ему на множестве всех действительных чисел.
Перенос члена неравенства (с противоположным знаком) из одной части неравенства в другую;
Умножение (деление) обеих частей неравенства на положительное число;
Применение правил умножения многочленов и формул сокращённого умножения;
Приведение подобных членов многочлена;
Возведение неравенства в нечётную степень;
Логарифмирование неравенства 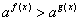 , т.е замена этого неравенства неравенством
, т.е замена этого неравенства неравенством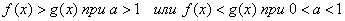
Назовем преобразования неравенств, приводящие исходное неравенство к неравенству равносильному ему на некотором множестве чисел
Возведение неравенства в чётную степень; (на множестве где обе функции неотрицательны)
Потенцирование неравенства; (на множестве где обе функции положительны)
Умножение обеих частей неравенства на функцию; (на множестве где функция положительна)
Применение некоторых формул (логарифмических, тригонометрических и др.) (на множестве где одновременно определены обе части применяемой формулы)
В зависимости от интерпретации неравенства различают
алгебраический
функциональный
графический
геометрический.
Среди алгебраических методов решения неравенств выделяют:
Сведение неравенства к равносильной системе или совокупности систем
Метод замены
Разбиение области определения неравенства на подмножества
Логарифмическое неравенство 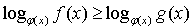 можно свести к равносильной совокупности систем неравенств
можно свести к равносильной совокупности систем неравенств
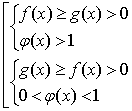
Решите неравенство:
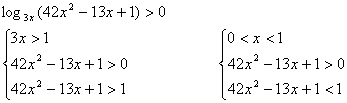
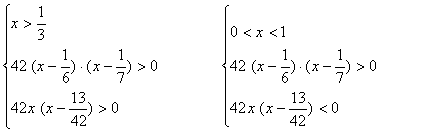
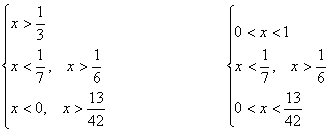

Ответ: 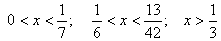
Оказывается, что данное неравенство можно решить иначе.
Зная свойства логарифма о том, что logа b 0, если a и b по одну сторону от 1, можно получить очень интересный и неожиданный способ решения неравенства. Об этом способе написано в статье “Некоторые полезные логарифмические соотношения” в журнале “Квант” № 10 за 1990 год.
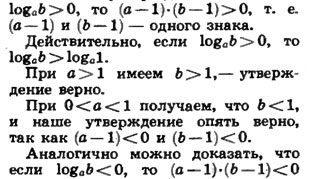
Решите это неравенство, используя новые соотношения
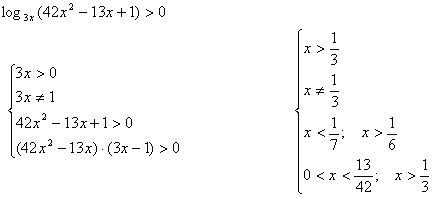
Ответ: 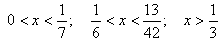
Оказывается, что при решении некоторых логарифмических неравенств можно использовать и другие соотношения
развернуть таблицу
| Заменяемое выражение | Используемое выражение |
| 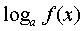
| 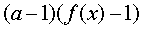
|
| 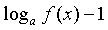
| 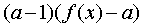
|
| 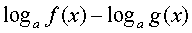
| 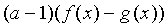
|
| 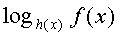
| 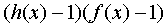
|
| 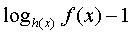
| 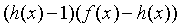
|
| 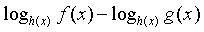
| 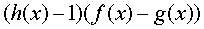
|
развернуть таблицу
Решите неравенство 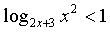
у доски составляем систему, которую решают самостоятельно
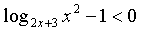
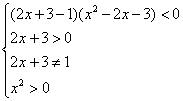
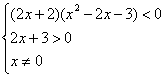
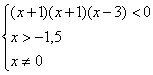
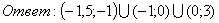

























 , т.е замена этого неравенства неравенством
, т.е замена этого неравенства неравенством
 можно свести к равносильной совокупности систем неравенств
можно свести к равносильной совокупности систем неравенств